【单调队列优化dp】jzoj3405舞台表演 纪中集训提高B组

Time Limits: 1000 ms Memory Limits: 524288 KB

Description

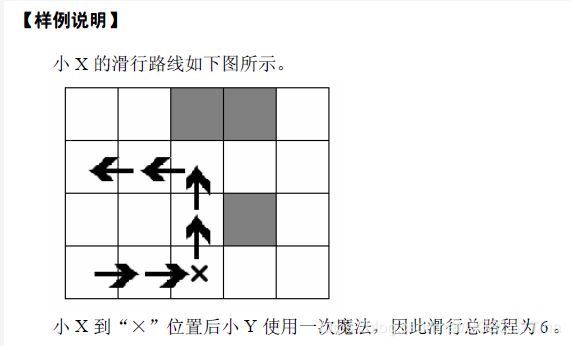
小X 终于找到了自己的舞台，希望进行一次尽兴的表演。

不妨认为舞台是一个n 行m 列的矩阵，矩阵中的某些方格上堆放了一些装饰物，其他的则是空地。小X 可以在空地上滑动，但不能撞上装饰物或滑出舞台，否则表演就失败了。

小Y 为了让小X 表演得尽量顺畅，提前为小X 写好了每一段时间的移动方向。每个时刻，听话的小X 都会依据小Y 写好的所在时间段的方向（东、西、南、北）向相邻的方格滑动一格。由于小Y 之前没有探查过舞台的情况，如果

小X 直接按照小Y 写好的来移动，很容易表演失败。

不过，小Y 是个天使，拥有让小X 停在原地的魔法，也就是某一时刻，小X 以为自己移动了实际上没有移动。为了让小X 表演得尽量完美，小Y 想使小X 在舞台上滑行的路程尽量长（当然不能中途表演失败）。可惜小Y 的智商不足

以完成这么复杂的计算，希望你来帮助她决定哪些时刻该使用魔法。当然，她关心的首先是最长的路程是多少。

Input

输入的第一行包含五个整数n,m, x, y 和k 。(x, y )为小 X的初始位置，k 为时间的段数。

接下来n 行每行包含m 个字符，描述这个舞台（“.”表示该位置是空地，“x”表示该位置有装饰物）。

接下来k 行每行包含三个整数si ti di (1<= i<= k )，表示在时间段[si,ti ] 内，小 X的移动方向是di 。di 为1,2,3,4中的一个，依次表示北、南、西、东（分别对应矩阵中的上、下、左、右）

Output

输出一行包含一个整数，表示小X 滑行的最长路程。

Sample Input

4 5 4 1 3

…xx.

…

…x.

…

1 3 4

4 5 1

6 7 3

Sample Output

6

Data Constraint

保证输入的时间段是连续的，即 s1 =1 ，si=ti-1+1(1

对于30%的数据，1≤ t ≤ 20。

对于60%的数据，1≤t ≤ 200。

对于100%的数据，1≤ n,m,k ≤ 200，1≤t ≤10^5。

Hint

---

考场上一来以为是水题，就在他要表演失败的时候使用魔法就可以了，数据只有1e5。
然而看了样例才发现我还是太年轻，太天真qwq
感觉是个dp，但看了数据范围猜测时间复杂度与t相关，想了一个$2^t$的爆搜
难道是启发式搜索？我都忘完了啊qwq

正解是单调队列优化dp，感觉很简单，四个方向一大波复制粘贴就可以了。听同学说何老师讲过，嘤嘤嘤我怎么不记得了，我只记得瑰丽华尔兹是这样滑来滑去不记得还有其他什么题也是滑来滑去的了2333。

话说当时考场上有这方面的想法来着，因为时间的范围太大了，就想着按段来，因为$k$比较小嘛。然而别人的$2^t$的暴力30分，我的$2^k$的暴力0分，也不知道为什么，难道是我写丑了？

切入正题。
定义$dp[k][i][j]$表示第$k$段时间走到点$(i,j)$的最长路径。
显然转移就是从上一段时间里面能够走到当前位置的$dp[k-1][i^{\prime }][j^{\prime }]+$从$(i^{\prime },j^{\prime })$走到当前位置的路径长的最大值。
就可以用单调队列维护。

#include
#include
#include
#include
using namespace std;
#define MAXN 205
#define LL long long
#define INF 0x3f3f3f3f
int n,m,x,y,k;
char mp[MAXN][MAXN];
int dp[MAXN][MAXN][MAXN];
int Q[MAXN];
int main()
{
	scanf("%d %d %d %d %d",&n,&m,&x,&y,&k);
	for(int i=1;i<=n;i++)
		scanf("%s",mp[i]+1);
	for(int t=0;t<=k;t++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=m;j++)
				dp[t][i][j]=-INF;
	dp[0][x][y]=0;
	for(int t=1;t<=k;t++)
	{
		int s,e,d;scanf("%d %d %d",&s,&e,&d);
		int len=e-s+1;
		if(d==1)
		{
			for(int j=1;j<=m;j++)
			{
				int head=1,tail=0;
				for(int i=n;i>=1;i--)
				{
					if(mp[i][j]=='x') {head=1,tail=0;continue;}
					while(head<=tail&&dp[t-1][i][j]>=dp[t-1][Q[tail]][j]+Q[tail]-i)
						tail--;
					Q[++tail]=i;//先维护tail就可以处理这一段时间都原地不走的状态
					while(head<=tail&&Q[head]-i>len)
						head++; 
					dp[t][i][j]=max(dp[t][i][j],dp[t-1][Q[head]][j]+Q[head]-i);
				}
			}
		}
		if(d==2)
		{
			for(int j=1;j<=m;j++)
			{
				int head=1,tail=0;
				for(int i=1;i<=n;i++)
				{
					if(mp[i][j]=='x') {head=1,tail=0;continue;}
					while(head<=tail&&dp[t-1][i][j]>=dp[t-1][Q[tail]][j]+i-Q[tail])
						tail--;
					Q[++tail]=i;//先维护tail就可以处理这一段时间都原地不走的状态
					while(head<=tail&&i-Q[head]>len)
						head++; 
					dp[t][i][j]=max(dp[t][i][j],dp[t-1][Q[head]][j]+i-Q[head]);
				}
			}
		}
		if(d==3)
		{
			for(int i=1;i<=n;i++)
			{
				int head=1,tail=0;
				for(int j=m;j>=1;j--)
				{
					if(mp[i][j]=='x') {head=1,tail=0;continue;}
					while(head<=tail&&dp[t-1][i][j]>=dp[t-1][i][Q[tail]]+Q[tail]-j)
						tail--;
					Q[++tail]=j;//先维护tail就可以处理这一段时间都原地不走的状态
					while(head<=tail&&Q[head]-j>len)
						head++;
					dp[t][i][j]=max(dp[t][i][j],dp[t-1][i][Q[head]]+Q[head]-j);
				}
			}
		}
		if(d==4)
		{
			for(int i=1;i<=n;i++)
			{
				int head=1,tail=0;
				for(int j=1;j<=m;j++)
				{
					if(mp[i][j]=='x') {head=1,tail=0;continue;}
					while(head<=tail&&dp[t-1][i][j]>=dp[t-1][i][Q[tail]]+j-Q[tail])
						tail--;
					Q[++tail]=j;//先维护tail就可以处理这一段时间都原地不走的状态
					while(head<=tail&&j-Q[head]>len)
						head++;
					dp[t][i][j]=max(dp[t][i][j],dp[t-1][i][Q[head]]+j-Q[head]);
				}
			}
		}
	}
	int ans=-INF;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			ans=max(ans,dp[k][i][j]);
	printf("%d\n",ans);
	return 0;
}

经证实，这道题就是瑰丽华尔兹~~（当初是谁说瑰丽华尔兹要比这个难一些来着~~ ，而且瑰丽华尔兹的时间数据范围更小，但时间段的范围是一样的，所以用单调队列优化的效果是一样的。
这道题的代码，也能过瑰丽华尔兹。