半平面交

半平面：

     平面内的一条直线把这个平面分成两部分，每一部分对这个平面来说都是一个半平面。其中包含这条直线的半平面叫做闭半平面，不包含直线的叫做开半平面。

     在二维坐标平面下，由一条直线ax + by + c = 0分割出的两个半平面可以用ax + by + c >= 0和ax + by + c < 0表示。

 

半平面交：

     半平面交实际上是由多个直线组成的一个方程组，每一个方程对应平面上的一条直线，方程组对应二维坐标平面下的一个封闭的多边形区域。（类似于线性规划中的可行域）

 

多边形的核：

     多边形的核实际上是一个平面点集，该点集中的任意一点与多边形边界上任意一点的连线都处于这个多边形的内部。就类似于一个摄像头，将摄像头安装在多边形内核区域的任何一个位置，都一个看到多边形的任何一个地方。

     多边形的内核可以是一个点，可以是一条直线，也可以是一个平面区域。

 

求凸多边形的内核区域：

     先用一个顺时针或者逆时针的顺序，将最初的多边形的点集存储起来，然后按集合中的顺序依次取连续的两个点组成一条直线，用这条直线来切割原来的多边形，按照直线方向以及顺时针或逆时针的规律逐渐剔除掉原点集中不符合要求的点，并添入新的点，直到遍历完所有的点为止。

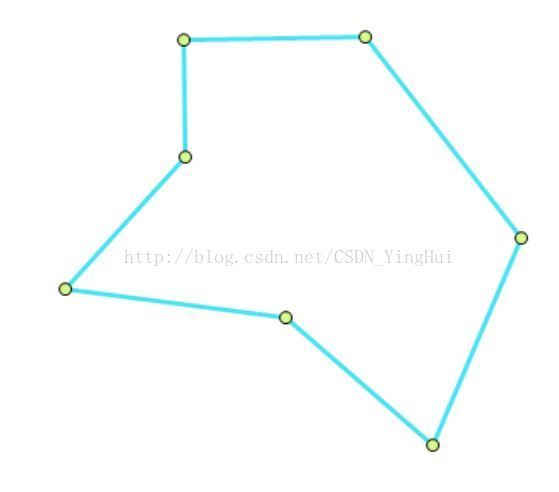
     以下图为例：

               

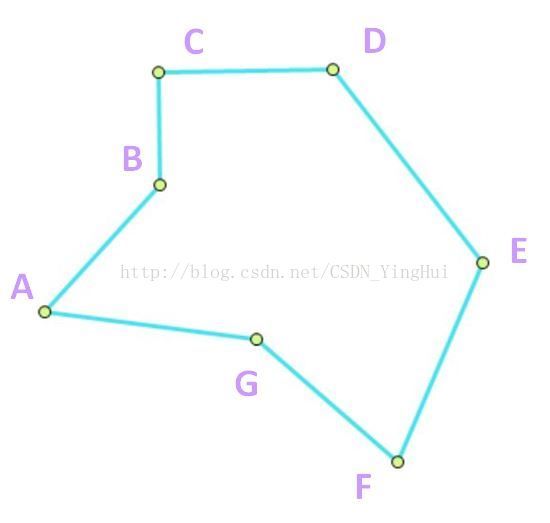
     按照顺时针的顺序给各点编号，如下图所示：

                     

     此时点集的顺序为：M = { A, B, C, D, E, F, G }

     同时内核点集初始化为：N = { A, B, C, D, E, F, G }

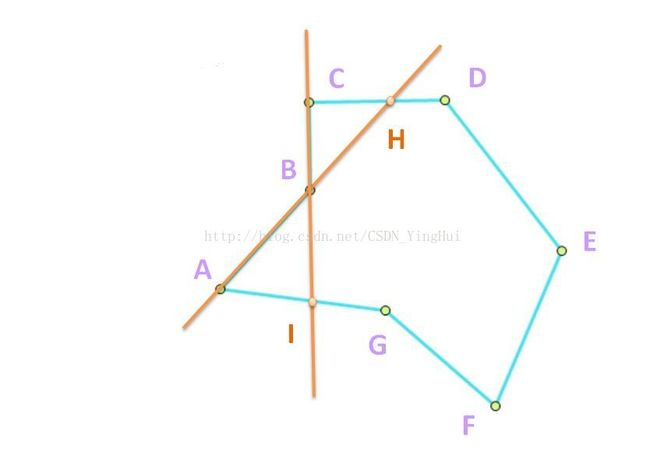
     按照各点在点集M中的顺序，依次连点成线，连接AB两点，组成直线AB，再将剩余的点依次带入直线AB中，发现C点带入后小于0，则C点不属于内核点集。同时，设直线AB交直线CD于一点H，则此时内核点集N更新为N = { A, B, H, D, E, F, G }

     PS：因为是按照顺时针排列的点，而且直线AB的方向为由A到B，所以应该取带入后大于0的点，即位于直线右侧的点。若是按照逆时针排列，则应该取位于直线左侧，带入直线方程后小于0的点。

    

     继续遍历M中的点，连接直线BC，发现带入A后直线小于0，则A不为内核点集中的点，同时直线BC交AG于一点I，则内核点集N更新为N = { B, H, D, E, F, G, I }

     

     由此依次遍历M中的点，直至连接GA，最后一次切割多边形，更新后的点集N即为符合题意的内核点集。

应用：

     半平面交主要用于求多边形的内核

例题：POJ 3130

AC代码：

#include
#include
#define zero 1e-8
#define INF 100000
using namespace std;

struct point
{
    double x, y;
} p[110], wa[110], wb[100], *a, *b;

int N, an, bn;

double fabs(double x)
{
    return x < 0 ? -x : x;
}

int dcmp(double x)
{
    return fabs(x) < zero ? 0 : (x < 0 ? -1 : 1);
}

double det(double x1, double y1, double x2, double y2)
{
    return x1 * y2 - x2 * y1;
}

void init()
{
    for(int i = 0; i < N; i ++)
        cin>>p[i].x>>p[i].y;

    p[N] = p[0];
}

void add(double x, double y)
{
    b[bn].x = x;
    b[bn].y = y;

    ++ bn;
}

void cut(int k)
{
    point *t;
    bn = 0;

    for(int i = 0; i < an; i ++)
    {
        int t1 = det(p[k + 1].x - p[k].x, p[k + 1].y - p[k].y, a[i].x - p[k].x, a[i].y - p[k].y);
        int t2 = det(p[k + 1].x - p[k].x, p[k + 1].y - p[k].y, a[i + 1].x - p[k].x, a[i + 1].y - p[k].y);

        if(dcmp(t1) >= 0)
            add(a[i].x, a[i].y);

        if(dcmp(t1) * dcmp(t2) < 0)
        {
            int x = (fabs(t2) * a[i].x + fabs(t1) * a[i + 1].x) / (fabs(t1) + fabs(t2));
            int y = (fabs(t2) * a[i].y + fabs(t1) * a[i + 1].y) / (fabs(t1) + fabs(t2));

            add(x, y);
        }
    }

    swap(a,b);
    swap(an,bn);

    a[an] = a[0];
}

void solve()
{
    a = wa, b = wb;
    an = 4;
    a[0].x = -INF, a[0].y = -INF;
    a[1].x = INF, a[1].y = -INF;
    a[2].x = INF, a[2].y = INF;
    a[3].x = -INF, a[3].y = INF;
    a[4] = a[0];

    for(int i = 0; i < N; i ++)
        cut(i);
    if(an == 0)
        cout<<"0"<> N;
        if(!N)
            break;
        init();
        solve();
    }
}