排序算法7——图解快速排序（两种主元选择方法）以及CUTOFF时间测试

排序算法1——图解冒泡排序及其实现（三种方法，基于模板及函数指针）
排序算法2——图解简单选择排序及其实现
排序算法3——图解直接插入排序以及折半（二分）插入排序及其实现
排序算法4——图解希尔排序及其实现
排序算法5——图解堆排序及其实现
排序算法6——图解归并排序及其递归与非递归实现
排序算法7——图解快速排序（两种主元选择方法）以及CUTOFF时间测试
排序算法8——图解表排序
排序算法9——图解桶排序及其实现
排序算法10——图解基数排序（次位优先法LSD和主位优先法MSD）
排序算法——比较与总结

---

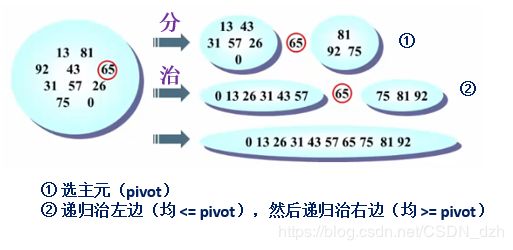
基本思想

通过一趟排序将待排记录分割成独立的两部分，
其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序

因此，快排的最好情况就是每次选主元的时候，正好是中分的。这样时间复杂度就是O（NlogN）

选主元

问题：

于是，选A[0]的方法就不太合适了，那么该如何选择呢？
这里使用取头中尾的中位数的方法：

子集划分

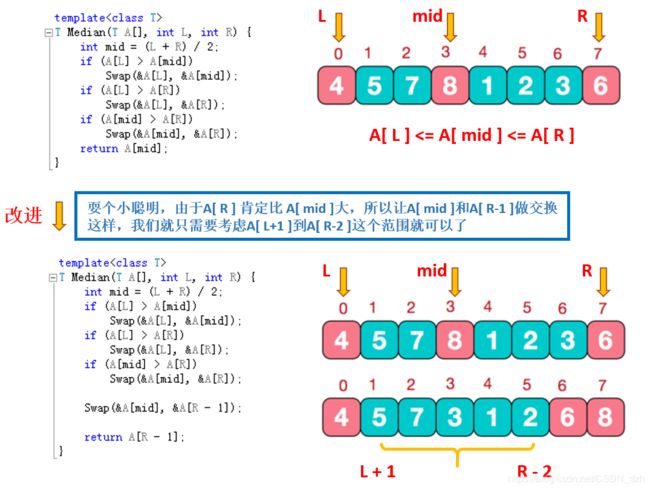
利用上面的方法，我们就得到了下面的主元6，并且将其放在倒数第二个位置（R-1）上，
这样，我们就只需要考虑i（L+1）到j（R-2）这个范围了
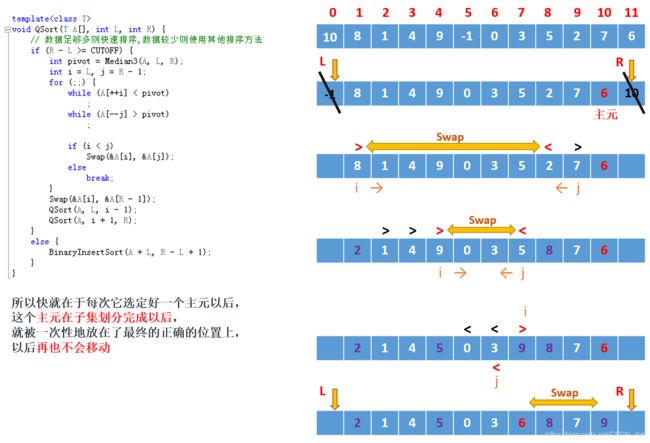
如果 i 指向的元素大于主元，则报红色，i停止往右，否则继续往右走
如果 j 指向的元素小于主元，则报红色，j停止往左，否则继续往左走
当i和j均停下的时候，如果 i < j，则交换两个元素，
这样，比主元小的元素就跑到了前面，比主元大的元素就跑到了后面
继续这一过程，若此时 i >= j了，则退出i和j相对行走的过程，
说明这一趟子集划分已经结束了，那么哪里是主元的正确位置？
然后交换i所指的元素和主元（因为此时 i 所指向的元素比主元大）

再考虑一个情况：
假如有元素等于主元pivot怎么办？（举一个元素全部相等的例子）
① 停下来交换？
这样的话子集划分基本上每一次都是相等的两份
② 不理它，继续移动指针？
这样的话i指针将一直往右走，而j指针根本没有机会移动，主元基本上都是在某一边的端点上，类似于之前讲的时间复杂度为O（N^2）
所以，两个里面的话，还是选第一种比较好

存在的问题

快速排序由于是用递归的方式实现的，它额外占用了系统堆栈的空间
对于小规模的数据（例如N不到100）可能还不如直接插入排序快
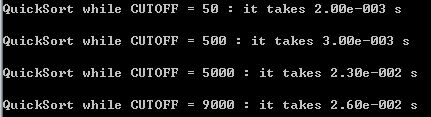
于是，我们设定了一个阈值CUTOFF，
当递归的数据规模小于该阈值的时候，停止递归，在这一层直接调用直接插入排序或二分排序图解插入排序
此时的起始位置为A+L， 终止位置为R-L+1

快排测试结果及代码

快速排序的测试结果如下,这里当序列长度小于阈值时，使用的是二分排序

#include 

const int CUTOFF = 5;

template<class T>
void Swap(T *a, T *b) {
	T tmp = *a;
	*a = *b;
	*b = tmp;
}

template<class T>
T Median3(T A[], int L, int R) {
	int mid = (L + R) / 2;
	if (A[L] > A[mid])
		Swap(&A[L], &A[mid]);
	if (A[L] > A[R])
		Swap(&A[L], &A[R]);
	if (A[mid] > A[R])
		Swap(&A[mid], &A[R]);

	Swap(&A[mid], &A[R - 1]);

	return A[R - 1];
}

template<class T>
void InsertSort(T A[], int N) {
	T tmp;
	int i, j;
	for (i = 1; i < N; ++i) {
		tmp = A[i];
		for (j = i; j > 0 && tmp < A[j - 1]; --j) {
			A[j] = A[j - 1];
		}
		A[j] = tmp;
	}
}

template<class T>
void BinaryInsertSort(T A[], int N) {
	int i, j, mid, left, right;
	T tmp;
	for (i = 1; i < N; ++i) {
		if (A[i] < A[i - 1])
			tmp = A[i];
		else
			continue;

		left = 0;
		right = i - 1;
		while (left <= right) {
			mid = (left + right) / 2;
			if (A[mid] > tmp)
				right = mid - 1;
			else
				left = mid + 1;
		}

		for (j = i; j > left; --j) {
			A[j] = A[j - 1];
		}
		A[left] = tmp;
	}
}

template<class T>
void QSort(T A[], int L, int R) {
	// 数据足够多则快速排序,数据较少则使用其他排序方法
	if (R - L >= CUTOFF) {
		int pivot = Median3(A, L, R);
		int i = L, j = R - 1;
		for (;;) {
			while (A[++i] < pivot)
				;
			while (A[--j] > pivot)
				;

			if (i < j)
				Swap(&A[i], &A[j]);
			else
				break;
		}
		Swap(&A[i], &A[R - 1]);
		QSort(A, L, i - 1);
		QSort(A, i + 1, R);
	}
	else {
		BinaryInsertSort(A + L, R - L + 1);
	}
}

template<class T>
void QuickSort(T A[], int N) {
	QSort(A, 0, N - 1);
}

template<class T>
void ArrShow(T *A, int length) {
	for (int i = 0; i < length; ++i) {
		std::cout << A[i] << " ";
	}
	puts("\n");
}

int main(int argc, char *argv[]) {
	int test[9] = { 1, 2, 7, 3, 8, 5, 9, 6, 4 };
	ArrShow(test, 9);

	puts("QuickSort : ");
	QuickSort(test, 9);
	ArrShow(test, 9);

	return 0;
}

---

CUTOFF测试结果及代码

不同的CUFOFF测试结果：

测试代码如下：

#include 
#include 

static int CUTOFF = 50;
const int SIZE = 10000;

template<class T>
void Swap(T *a, T *b) {
	T tmp = *a;
	*a = *b;
	*b = tmp;
}

template<class T>
T Median3(T A[], int L, int R) {
	int mid = (L + R) / 2;
	if (A[L] > A[mid])
		Swap(&A[L], &A[mid]);
	if (A[L] > A[R])
		Swap(&A[L], &A[R]);
	if (A[mid] > A[R])
		Swap(&A[mid], &A[R]);

	Swap(&A[mid], &A[R - 1]);

	return A[R - 1];
}

template<class T>
void InsertSort(T A[], int N) {
	T tmp;
	int i, j;
	for (i = 1; i < N; ++i) {
		tmp = A[i];
		for (j = i; j > 0 && tmp < A[j - 1]; --j) {
			A[j] = A[j - 1];
		}
		A[j] = tmp;
	}
}

template<class T>
void BinaryInsertSort(T A[], int N) {
	int i, j, mid, left, right;
	T tmp;
	for (i = 1; i < N; ++i) {
		if (A[i] < A[i - 1])
			tmp = A[i];
		else
			continue;

		left = 0;
		right = i - 1;
		while (left <= right) {
			mid = (left + right) / 2;
			if (A[mid] > tmp)
				right = mid - 1;
			else
				left = mid + 1;
		}

		for (j = i; j > left; --j) {
			A[j] = A[j - 1];
		}
		A[left] = tmp;
	}
}

template<class T>
void QSort(T A[], int L, int R) {
	// 数据足够多则快速排序,数据较少则使用其他排序方法
	if (R - L >= CUTOFF) {
		int pivot = Median3(A, L, R);
		int i = L, j = R - 1;
		for (;;) {
			while (A[++i] < pivot)
				;
			while (A[--j] > pivot)
				;

			if (i < j)
				Swap(&A[i], &A[j]);
			else
				break;
		}
		Swap(&A[i], &A[R - 1]);
		QSort(A, L, i - 1);
		QSort(A, i + 1, R);
	}
	else {
		BinaryInsertSort(A + L, R - L + 1);
	}
}

template<class T>
void QuickSort(T A[], int N) {
	QSort(A, 0, N - 1);
}

template<class T>
void ArrCreate(T *A, int length) {
	for (int i = 0; i < length; ++i) {
		A[i] = rand() % length;
	}
}

template<class T>
void ArrShow(T *A, int length) {
	for (int i = 0; i < length; ++i) {
		std::cout << A[i] << " ";
	}
	puts("\n");
}

template<class T>
void ArrCopy(T *copy, T *A, int length) {
	for (int i = 0; i < length; ++i) {
		copy[i] = A[i];
	}
}

int main(int argc, char *argv[]) {


	int test_50[SIZE] = { 0 };
	int test_500[SIZE] = { 0 };
	int test_5000[SIZE] = { 0 };
	int test_9000[SIZE] = { 0 };

	ArrCreate(test_50, SIZE);
	ArrCopy(test_500, test_50, SIZE);
	ArrCopy(test_5000, test_50, SIZE);
	ArrCopy(test_9000, test_50, SIZE);

	clock_t start, stop;
	double duration = 0;
	start = clock();
	QuickSort(test_50, SIZE);
	stop = clock();
	duration = ((double)(stop - start)) / CLK_TCK;
	printf("QuickSort while CUTOFF = 50 : it takes %6.2e s \n\n", duration);

	CUTOFF = 500;
	start = clock();
	QuickSort(test_500, SIZE);
	stop = clock();
	duration = ((double)(stop - start)) / CLK_TCK;
	printf("QuickSort while CUTOFF = 500 : it takes %6.2e s \n\n", duration);

	CUTOFF = 5000;
	start = clock();
	QuickSort(test_5000, SIZE);
	stop = clock();
	duration = ((double)(stop - start)) / CLK_TCK;
	printf("QuickSort while CUTOFF = 5000 : it takes %6.2e s \n\n", duration);

	CUTOFF = 9000;
	start = clock();
	QuickSort(test_9000, SIZE);
	stop = clock();
	duration = ((double)(stop - start)) / CLK_TCK;
	printf("QuickSort while CUTOFF = 9000 : it takes %6.2e s \n\n", duration);

	return 0;
}

简单实现版（首元素作主元和三数取中作主元）

首元素作主元

#include  
#include 
using namespace std;

int pivot1(int a[], int L, int R) {
	return a[L];
}

void Swap(int *a, int *b) {
	int t = *a;
	*a = *b;
	*b = t;
}

void Qsort1(int a[], int L, int R) {
	if (L < R) {
		int p = pivot1(a, L, R);
		int i = L + 1;
		int j = R;

		for (;;) {
			while (a[i] < p)
				i++;
			while (a[j] > p)
				j--;

			if (i < j)
				Swap(&a[i++], &a[j--]);
			else
				break;
		}
		Swap(&a[j], &a[L]);
		Qsort1(a, L, j - 1);
		Qsort1(a, i, R);
	}	
}

int main() {
	
	const int N = 9;
	int a[N] = { 0 };
	srand(time(NULL));

	for (int i = 0; i < N; ++i) {
		for (int j = 0; j < N; ++j) {
			a[j] = rand() % 100 + 1;	// 产生1-100随机数
		}
		cout << "第" << i << "次:";
		for (int k = 0; k < N; ++k) {
			cout << " " << a[k];
		}	
		cout << "------>排序结果 :";

		Qsort1(a, 0, N - 1);
		for (int x = 0; x < N; ++x) {
			cout << " " << a[x];
		}
		cout << endl;
	}

	return 0;
}

三数取中作主元

#include  
#include 
using namespace std;

void Swap(int *a, int *b) {
	int t = *a;
	*a = *b;
	*b = t;
}

int median(int a[], int L, int R) {
	int Mid = (L + R) / 2;
	if (a[L] > a[Mid])
		Swap(&a[L], &a[Mid]);
	if (a[L] > a[R])
		Swap(&a[L], &a[R]);
	if (a[Mid] > a[R])
		Swap(&a[R], &a[Mid]);
	Swap(&a[R - 1], &a[Mid]);
	return a[R - 1];
}

void Qsort2(int a[], int L, int R) {
	if (L < R) {
		int p = median(a, L, R);
		int i = L;
		int j = R - 2;
		for (;;) {
			while (a[i] < p)
				i++;
			while (a[j] > p)
				j--;
			if (i < j)
				Swap(&a[i], &a[j]);
			else
				break;
		}
		Swap(&a[i], &a[R - 1]);
		Qsort2(a, L, i - 1);
		Qsort2(a, i + 1, R);
	}
}

int main() {
	
	const int N = 9;
	int a[N] = { 0 };
	srand(time(NULL));

	for (int i = 0; i < N; ++i) {
		for (int j = 0; j < N; ++j) {
			a[j] = rand() % 100 + 1;	// 产生1-100随机数
		}
		cout << "第" << i << "次:";
		for (int k = 0; k < N; ++k) {
			cout << " " << a[k];
		}	
		cout << "------>排序结果 :";

		Qsort2(a, 0, N - 1);
		for (int x = 0; x < N; ++x) {
			cout << " " << a[x];
		}
		cout << endl;
	}

	return 0;
}