搜索问题:DFS 与 BFS
搜索
搜索算法是利用计算机的高性能来有目的的穷举一个问题解空间的部分或所有的可能情况,从而求出问题的解的一种方法。搜索算法实际上是根据初始条件和扩展规则构造一棵“解答树”并寻找符合目标状态的节点的过程。所有的搜索算法从最终的算法实现上来看,都可以划分成两个部分——扩展节点的方式和扩展节点,而所有的算法优化和改进主要都是通过修改其控制结构来完成的。其实,在这样的思考过程中,我们已经不知不觉地将一个具体的问题抽象成了一个图论的模型——树,即搜索算法的使用第一步在于搜索树的建立。
经典问题
- n^2-1数码难题(n=8,15,24……)
- 迷宫求生
- 黑白棋游戏
dfs与bfs
在这里,小编根据最近编程获得的一点点经验谈一谈搜索算中的最基本两种——深度优先(dfs)与宽度优先(bfs)
关于dfs与bfs的大致定义和特点,我相信广大读者能够通过下列八数码难题的搜索树建立过程迅速了解,小编就不多说了
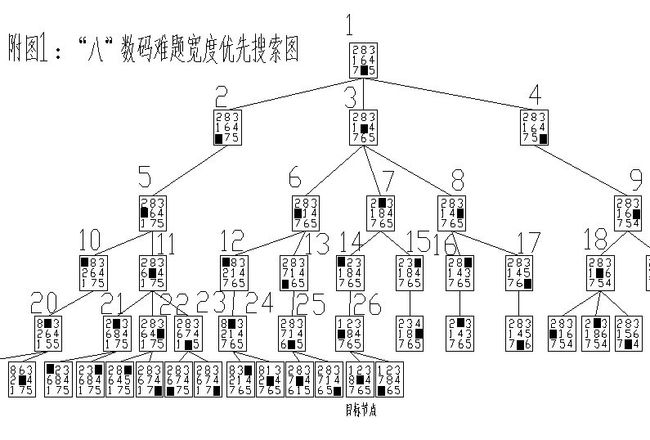
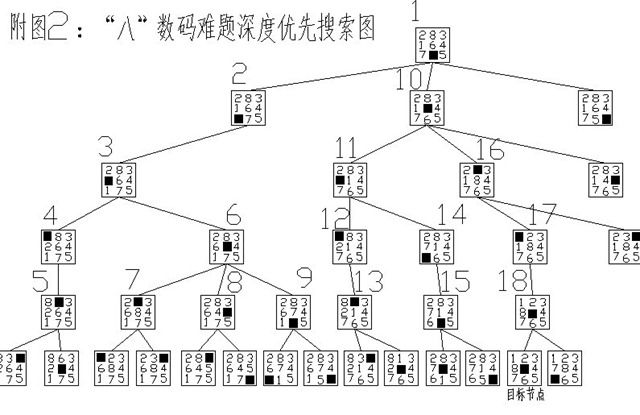
dfs与bfs有各自的有点也有各自的缺点,我们要根据待求解问题的性质来决定选择哪种搜索方式
选择dfs的情况:
1. 当最大深度确定,只要知道问题有没有解
2. 当最大深度确定,只要求出一个或部分解时
选择bfs的情况:
1、当要求出问题最优解(树的深度最小)
2、需要求出问题的全部解时(dfs也可)
bfs需要拓展所有节点,随着结点在搜索树上的深度增大,搜索的结点数会很快增长,并以指数形式扩张,从而所需的存储空间和搜索花费的时间也会成倍增长。所以在不需要求得最短路径的情况下小编建议使用dfs
为了更好的说明以上观点,小编这里引用了三个case,并附上了小编的AC代码,以及辅助说明代码
#Case1:Tempter of the Bone
Problem Description
The doggie found a bone in an ancient maze, which fascinated him a lot. However, when he picked it up, the maze began to shake, and the doggie could feel the ground sinking. He realized that the bone was a trap, and he tried desperately to get out of this maze.
The maze was a rectangle with sizes N by M. There was a door in the maze. At the beginning, the door was closed and it would open at the T-th second for a short period of time (less than 1 second). Therefore the doggie had to arrive at the door on exactly the T-th second. In every second, he could move one block to one of the upper, lower, left and right neighboring blocks. Once he entered a block, the ground of this block would start to sink and disappear in the next second. He could not stay at one block for more than one second, nor could he move into a visited block. Can the poor doggie survive? Please help him.
Input
The input consists of multiple test cases. The first line of each test case contains three integers N, M, and T (1 < N, M < 7; 0 < T < 50), which denote the sizes of the maze and the time at which the door will open, respectively. The next N lines give the maze layout, with each line containing M characters. A character is one of the following:
‘X’: a block of wall, which the doggie cannot enter;
‘S’: the start point of the doggie;
‘D’: the Door; or
‘.’: an empty block.
The input is terminated with three 0’s. This test case is not to be processed.
Output
For each test case, print in one line “YES” if the doggie can survive, or “NO” otherwise.
Sample Input
4 4 5
S.X.
..X.
..XD
….
3 4 5
S.X.
..X.
…D
0 0 0
Sample Output
NO
YES
Case1只要得到doggie是否能走出迷宫,不需要知道全部解,因此采用dfs的方式
//Title:AC code
//Author:Call偶围城
#include #Case2:Prime Ring Problem
Problem Description
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, …, n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
Note: the number of first circle should always be 1.
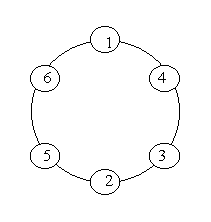
Input
n (0 < n < 20).
Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
6
8
Sample Output
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
Case2要求给出所有解,dfs和bfs都可取,小编这里采取用dfs
//Title:AC code
//Author:Call偶围城
#include #Case3:Nightmare
Problem Description
Ignatius had a nightmare last night. He found himself in a labyrinth with a time bomb on him. The labyrinth has an exit, Ignatius should get out of the labyrinth before the bomb explodes. The initial exploding time of the bomb is set to 6 minutes. To prevent the bomb from exploding by shake, Ignatius had to move slowly, that is to move from one area to the nearest area(that is, if Ignatius stands on (x,y) now, he could only on (x+1,y), (x-1,y), (x,y+1), or (x,y-1) in the next minute) takes him 1 minute. Some area in the labyrinth contains a Bomb-Reset-Equipment. They could reset the exploding time to 6 minutes.
Given the layout of the labyrinth and Ignatius’ start position, please tell Ignatius whether he could get out of the labyrinth, if he could, output the minimum time that he has to use to find the exit of the labyrinth, else output -1.
Here are some rules:
1. We can assume the labyrinth is a 2 array.
2. Each minute, Ignatius could only get to one of the nearest area, and he should not walk out of the border, of course he could not walk on a wall, too.
3. If Ignatius get to the exit when the exploding time turns to 0, he can’t get out of the labyrinth.
4. If Ignatius get to the area which contains Bomb-Rest-Equipment when the exploding time turns to 0, he can’t use the equipment to reset the bomb.
5. A Bomb-Reset-Equipment can be used as many times as you wish, if it is needed, Ignatius can get to any areas in the labyrinth as many times as you wish.
6. The time to reset the exploding time can be ignore, in other words, if Ignatius get to an area which contain Bomb-Rest-Equipment, and the exploding time is larger than 0, the exploding time would be reset to 6.
Input
The input contains several test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow.
Each test case starts with two integers N and M(1<=N,Mm=8) which indicate the size of the labyrinth. Then N lines follow, each line contains M integers. The array indicates the layout of the labyrinth.
There are five integers which indicate the different type of area in the labyrinth:
0: The area is a wall, Ignatius should not walk on it.
1: The area contains nothing, Ignatius can walk on it.
2: Ignatius’ start position, Ignatius starts his escape from this position.
3: The exit of the labyrinth, Ignatius’ target position.
4: The area contains a Bomb-Reset-Equipment, Ignatius can delay the exploding time by walking to these areas.
Output
For each test case, if Ignatius can get out of the labyrinth, you should output the minimum time he needs, else you should just output -1.
Sample Input
3
3 3
2 1 1
1 1 0
1 1 3
4 8
2 1 1 0 1 1 1 0
1 0 4 1 1 0 4 1
1 0 0 0 0 0 0 1
1 1 1 4 1 1 1 3
5 8
1 2 1 1 1 1 1 4
1 0 0 0 1 0 0 1
1 4 1 0 1 1 0 1
1 0 0 0 0 3 0 1
1 1 4 1 1 1 1 1
Sample Output
4
-1
13
Case3要求给出最短路径,比较典型的使用bfs的案例
//Title:AC code
//Author:Call偶围城
#include
小编再给一个用C++实现求解的AC code,C++自带queue,不需要自己实现队列存储及队列操作
//Title:AC code
//Author:auto
# include else cout<return 0;
}
另外,小编再给大家看看如果用dfs求解这个问题的代码,比bfs复杂很多
在使用dfs时,小编遇到的困难有:
-为了防止死循环,所以 当Ignatius走到一个Bomb-Reset-Equipment上时,这个结点的子辈结点都不能再使用这个Bomb-Reset-Equipment,而这个结点的兄弟结点和父辈结点的兄弟结点仍可以使用,所以在递归和回溯时要把控制Bomb-Reset-Equipment是否可用的变量修改(reset[i][j]–/reset[i][j]++,当reset[i][j]=1时maze[i][j]的Bomb-Reset-Equipment才可用);而bfs中只要有一个结点访问过Bomb-Reset-Equipment就可把这个Bomb-Reset-Equipment视为EMPTY
- 如果要进行剪枝,dfs比较困难,需要再定义一个vis地图保存访问记录,当Ignatius走到Bomb-Reset-Equipment上时还要允许Ignatius可以回退两步(BACK),不仅情况复杂,而且占用内存空间比较大;而bfs如果要剪枝的话只需要保存其父结点(之后我会给出带剪枝的bfs和dfs的code),当Ignatius走到Bomb-Reset-Equipment上时只要把此结点的父结点指向自己即可
- 查找次数过多
—- | Case1 | Case1 | Case1 |
bfs |—– 34 |—-119 |— 164 |
dfs |—– 36 |—-989 |— 564 |
//Title:dfs
//Author:Call偶围城
#include
下面小编给大家展示带剪枝的bfs和dfs
//Title:bfs with bounds & constraints
//Author:Call偶围城
#include //Title:dfs with bounds & constraints
//Author:Call偶围城
#include 以下是各类搜索在案例测试中的搜索次数的比较:
—- | Case1 | Case1 | Case1 |
without bounds or constrains
bfs |—– 34 |—-119 |— 164 |
dfs |—– 36 |—-989 |— 564 |
with bounds and constrains
bfs |—– 10 |—— 14|—- 32 |
dfs |—– 23 |—— 35|—- 57 |
关于Case3,小编最后还要说几句:
- 剪枝很重要
- 当求最短路径时,用bfs绝对比dfs好,尤其是程序出bug后,打印调试时,dfs几百行的数据一条条验证小编的内心是崩溃的。。。
- 未剪枝的dfs应该可以AC,如果不考虑时间限制
- 最后两个剪枝的bfs和dfs并没有AC==,不知道为什么,如果有大神看出来请留言赐教OO
注:读者可以进一步了解其他常用的搜索算法,如双向宽度优先搜索,启发式搜索(A*算法)。小编在整理时看到一篇比较好的博客,在这里推荐给大家
http://blog.csdn.net/huangxy10/article/details/8034285
博主用C++对象的形式,以八数码问题为案例展示了各类搜索算法
——1010,1016,1072