【CS229 Deep Learning笔记】一. 介绍：线性回归问题
注：该笔记主要以我自己的个人理解为主，部分基础知识会有省略，有些地方会有补充，小标题不完全按照课程pdf的顺序。笔记仅作参考，还是建议大家以课程pdf为主。
最后我会附上带有书签的课程pdf（2017年秋季课程），及problem set答案。如果有疑问，欢迎大家留言或私信讨论。
另，第一章虽然是介绍，但内容非常多，我会分为3篇博客来发。
目录
零·基础知识
一·线性回归
1. 梯度下降基本算法
2. 另一种梯度下降策略——随机梯度下降
（1）批量梯度下降
（2）随机梯度下降
3. 正规方程（normal equation）
二. 对J和线性回归的一个解释
三. 局部权重线性回归（locally weighted linear regression）
零·基础知识
（图源自CS 229课程pdf）
统计学习方法的大致过程如上所示，训练集（Training set）通过算法训练(Learning algorithm)得到假说h（hypothesis）。在测试集中，输入x得到预测值y。我们的目标是在拥有训练集和测试集的情况下，求得假说h，使得h能准确预测y|x。
这些问题往往可以分为两大类，回归问题和分类问题。
一·线性回归
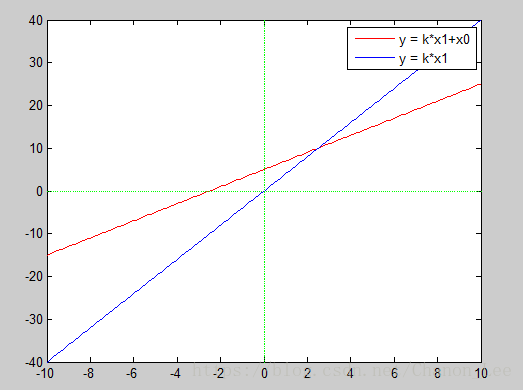
形如
的问题被称为线性回归问题。x为n维向量，每一维对应不同的输入特征。如在住房价格预测问题中，x1是房屋面积，x2是房屋数量。在实际应用中，我们会在x之前加上一个1，即设
为1，使预测函数可以在平面上自由移动，不必非得通过原点。
为了解y的预测值与实际值的差距，我们定义损失函数为：
损失函数（cost function）有时也叫风险函数，在不同的翻译中也有别的叫法，但一般都是以
来表示，大家可以从这一点来判断。另外，损失函数也可以有别的计算方式，但用得最多的就是均方差的形式。本节中只使用该误差函数。
结合刚才介绍的假说h，我们的目标就是调整h的参数使损失函数J尽可能小（即预测值与实际值的差距尽可能小），由此得到假说h。
1. 梯度下降基本算法
输入：训练集
输出：参数θ
1.令θ=0；
2.计算
3.令
，若达到迭代次数，或
4.输出θ
在该问题中，关键在于求梯度
。在本节中，我们使用均方差来定义损失函数，即。
现求解如下：
（图源自CS229）
可得
。将上式代入开头的算法，即可得到具体的迭代公式。今后学习的算法中，一部分算法的思路跟上面算法相同，只是与θ的迭代式不同。
2. 另一种梯度下降策略——随机梯度下降
（1）批量梯度下降
在刚才介绍的算法中，我们要求同时更新每一个θ的值，不能每更新一个
的值，就重新计算J，再去更新下一个
。这称为批量梯度下降（batch gradient descent）这种方法的缺点在于，每一次更新都需要计算全部训练集，计算量非常大。于是人们提出了随机梯度下降。
输入：训练集
输出：参数θ
1.令θ=0；
2.计算
3.对每一个j，令
4.输出θ
（2）随机梯度下降
随机梯度下降(stochastic gradient descent)每次只计算一个训练样例，以此来更新所有参数。
输入：训练集
输出：参数θ
1.令θ=0；
2. For i to m，计算
。 对每一个j，令
3. 输出θ
3. 正规方程（normal equation）
除梯度下降法以外，还有一种方法可以最小化误差函数J。构造输入矩阵X，X为m×（n+1）矩阵。M为训练集中的例子数量，n为每个例子的特征数量（如，身高，体重，就是2个特征）。其中的1是为每个例子前面加的一个1，其作用在线性回归中已经解释过了，是为了让回归函数h能在空间中自由移动，准确地进行预测。
将损失函数写为矩阵形式，得到
于是，对梯度的求导也可写为矩阵形式：
（图源自CS229）
（具体的推导和证明可以去看原来课程的pdf和矩阵知识的补充，在此不做赘述。）
我们假设为凸函数，仅有一个极小值点，当梯度为0时J取得极小值（也是最小值）。令上面的梯度为0，得到下式
该式即为正规方程。
二. 对J和线性回归的一个解释
为什么J要取均方差？为什么要使用线性回归？以下是一个可能的解释。
假设一：设
，其中ε为误差项，或者说是随机噪声。
假设二：ε服从均值为0、方差为
的高斯分布。
即
。考虑到
，可得
求得该分布的似然函数为
为方便计算，取对数。
求似然函数的最大值等价于求
的最小值。
所以，其实上面所列举的算法核心思想不是“使误差函数最小”，而是“在输入x的情况下，令结果为y的可能性最大，求得此时的θ”。求最小误差函数不过是这种思想下的一种表象，如果不理解似然函数，就不能理解为什么要使用这样或那样的误差函数，也不能理解为什么要使用各种不同形式的模型。
虽然Andrew Ng说这只是一个可能的解释，但其实这种思想在后面介绍的算法中有着非常多的运用。等以后遇到了我们再进行对比。
三. 局部权重线性回归（locally weighted linear regression）
原有线性回归：
局部权重线性回归：
局部权重线性回归是为解决过拟合的问题提出的。对某一个i，
越大，我们会越努力地使该训练例的误差
变小。越小，我们就会忽略该训练例的误差。
一个对的选择是
x为我们选定的点，若该例子离x越远，该值的权重越小。若该例子离x越近，该值的权重越大。
为带宽。这种方法下，我们主要考虑x附近的点的影响，很少考虑远离x的点。
输入：训练集
输出：参数θ
1.令θ=0；
2.计算
3.对每一个j，令
，若达到迭代次数，或
4.输出θ
该算法也属于梯度下降算法，但由于不同，带入求得的迭代式也不同。总体来说，跟前面的方法大同小异。
疑问：该方法可否用正规方程求解呢？