简析平衡树(三)——浅谈Splay
前言
原本以为 T r e a p Treap Treap已经很难了,学习了 S p l a y Splay Splay,我才知道,没有最难,只有更难。(强烈建议先去学一学 T r e a p Treap Treap再来看这篇博客)
简介
S p l a y Splay Splay是平衡树中的一种,除了平衡树所共有的作用之外,它还可以维护区间翻转,这也是它能成为 L C T LCT LCT辅助树的原因(不过 L C T LCT LCT并不是这篇博客所探讨的内容)。
因此,这篇博客将分为三个部分,第一个部分讲讲 S p l a y Splay Splay与其他平衡树的不同之处,另外两个部分则分别借助两道模板题,来讲讲 S p l a y Splay Splay两方面的作用。
S p l a y Splay Splay与其他平衡树的不同之处
s p l a y splay splay这个单词在百度翻译上的解释是张开。而在这里,则是指伸展(其实伸展与张开差不多)。
S p l a y Splay Splay最重要的操作自然就是伸展操作了。
而伸展操作,则是建立于类似于 T r e a p Treap Treap的 R o t a t e Rotate Rotate旋转操作上的。
R o t a t e Rotate Rotate操作在简析平衡树(二)中已经介绍过了,这里就直接贴代码了:
inline void Rotate(int x,int &k)//好吧,两个Rotate操作还是有点区别的,因为Splay还要记录每个节点的父亲,这里的Rotate是要将x节点向上旋转一位,而k则是要旋转到的目标位置
{
int fa=node[x].Father,grandpa=node[fa].Father,d=Which(x);//我们用fa记录当前节点的父亲,grandpa记录当前节点的祖父,d记录当前节点是父亲的哪一个儿子
if(fa^k) node[grandpa].Son[Which(fa)]=x;//如果当前节点的父亲不是目标位置,那么更新当前节点祖父的儿子为当前节点
else k=x;//否则说明已到达目标位置
node[x].Father=grandpa,node[fa].Son[d]=node[x].Son[d^1],node[node[x].Son[d^1]].Father=fa,node[x].Son[d^1]=fa,node[fa].Father=x,PushUp(fa),PushUp(x);//这个与Treap中的操作差不多,先将当前节点的父亲更新为当前节点的祖父,并将当前节点原先父亲这一位的儿子更新为当前节点与这个方向相反的儿子,并将当前节点原先的父亲更新为当前节点的儿子,最后记得更新节点信息
}
而 S p l a y Splay Splay的主要功能,就是通过不断地 R o t a t e Rotate Rotate,使某一节点旋转至目标位置。
我们可以对 S p l a y Splay Splay每次的旋转操作进行分类讨论:
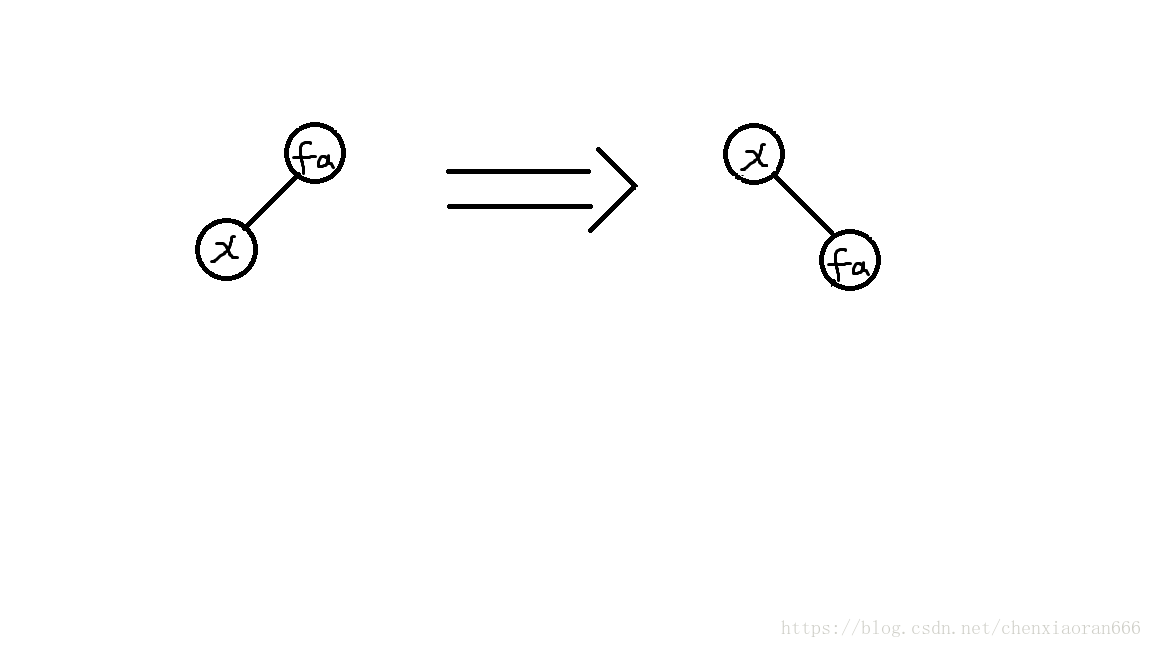
第一种情况, f a fa fa即为目标位置,此时只要上旋 x x x即可到达目标位置。
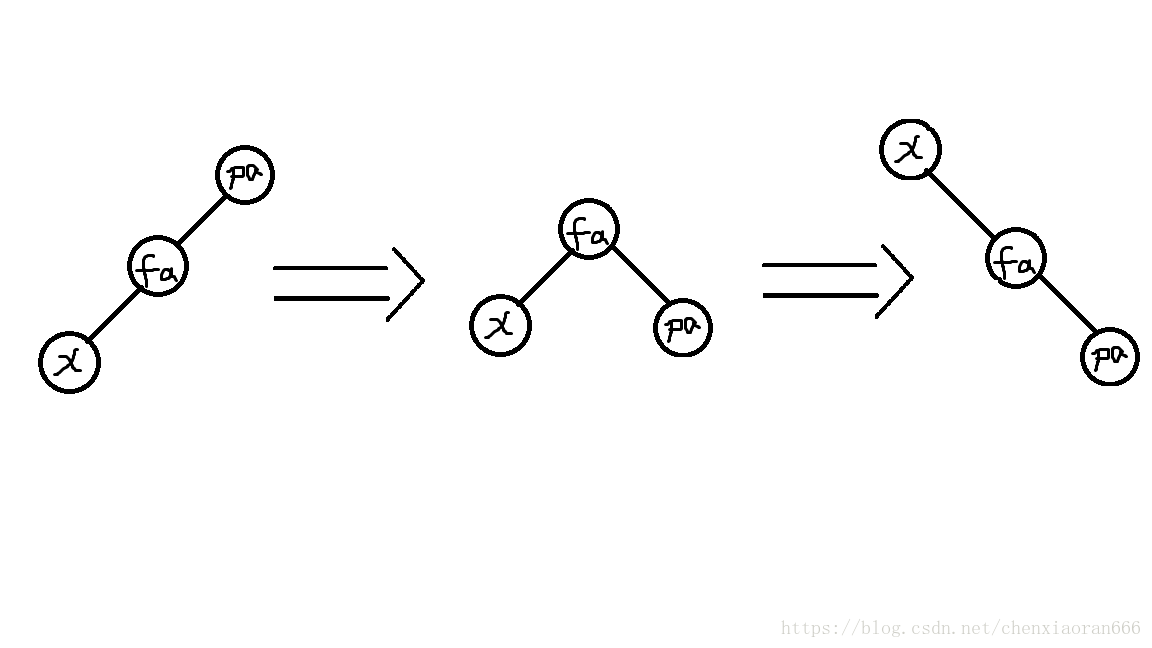
第二种情况, x x x, f a fa fa, g r a n d p a grandpa grandpa在同一直线上,且 f a fa fa不为目标位置。此时,我们需要将 f a fa fa上旋,同时带动 x x x上旋,然后再上旋一遍x。
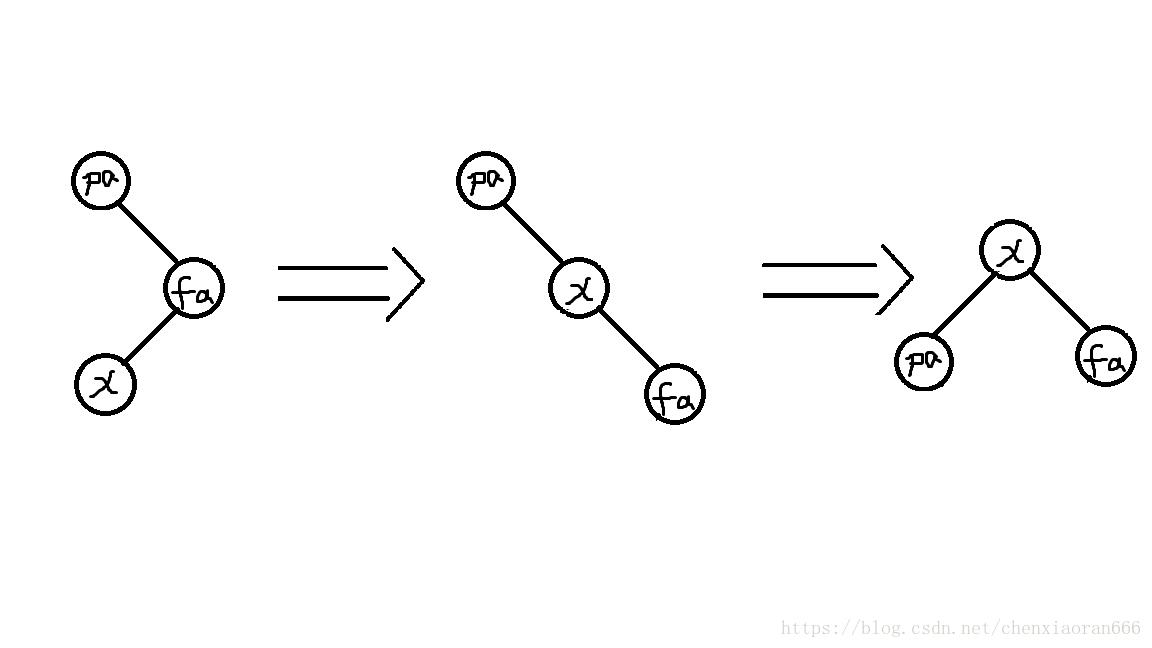
第三种情况, x x x, f a fa fa, g r a n d p a grandpa grandpa不在同一直线上,且 f a fa fa不为目标位置。此时,我们直接将 x x x上旋,将 x x x的父亲更新为它的祖父 g r a n d p a grandpa grandpa,然后再上旋一遍 x x x即可。
具体代码实现如下:
inline void Splay(int x,int &k)//将x一直旋转到目标位置k
{
for(int fa=node[x].Father;x^k;fa=node[x].Father)//重复循环,直至x为k
{
if(fa^k) Rotate(Which(fa)^Which(x)?x:fa,k);//如果fa不是目标位置,若x,fa,grandpa在同一直线上,我们需要将fa上旋,否则,直接将x上旋
Rotate(x,k);//归纳可以得出,不管什么情况下都要将x上旋
}
}
讲完了 S p l a y Splay Splay与其他平衡树的不同之处,后面的就很简单了。
模板1:【洛谷3369】【模板】普通平衡树
这应该是我第三次用到这个模板了,每学一种平衡树,都要过一次这个模板。
借助这个模板,我们主要研究的是 S p l a y Splay Splay作为平衡树的必有功能: B S T BST BST的功能。
不得不说,在插入和查询这两方面, S p l a y Splay Splay和 B S T BST BST还是十分像的,唯一区别是,每次插入/查询结束后,都要用 S p l a y Splay Splay操作将当前操作的点旋转到根。
为什么要这么做呢?
因为这样就使得 S p l a y Splay Splay的形状在不停地变化,即使在某一时刻成了一条链,下一刻一定又会变成其他形状,就很难被卡掉了。
插入/查询代码如下:
inline void Insert(int &x,int val,int fa)//插入一个数
{
if(!x)//如果当前节点为空
{
node[x=++tot].Val=val,node[x].Cnt=node[x].Size=1,node[x].Father=fa,node[x].Son[0]=node[x].Son[1]=0,Splay(x);//将元素插入这个节点,并将其旋转到根
return;
}
if(node[x].Val==val) ++node[x].Cnt,PushUp(x),PushUp(node[x].Father),Splay(x);//如果当前元素等于插入元素,就将当前元素的出现次数加1,并将当前节点旋转到根
else if(node[x].Val>val) Insert(node[x].Son[0],val,x);//否则,如果当前元素大于插入元素,就将插入元素插入至当前元素的左子树(遵循BST的基本性质嘛)
else Insert(node[x].Son[1],val,x);//否则,插入当前元素的右子树
}
inline int get_rank(int val)//询问值为val的数的排名
{
int x=rt,rk=0;
while(x)//只要当前节点不是空节点
{
if(node[x].Val==val) {rk+=node[node[x].Son[0]].Size,Splay(x);return rk+1;}//若当前元素与查询元素值相等,那么将它旋转到根节点,并返回答案
else if(node[x].Val>val) x=node[x].Son[0];//否则,如果当前元素大于插入元素,就访问当前元素的左子树
else rk+=node[node[x].Son[0]].Size+node[x].Cnt,x=node[x].Son[1];//否则,更新排名,并访问右子树
}
}
inline int get_val(int rk)//询问排名为rk的数的值
{
int x=rt;
while(x)
{
if(node[node[x].Son[0]].Size>=rk) x=node[x].Son[0];//如果当前节点左子树大小大于等于rk,说明答案在左子树
else if(node[node[x].Son[0]].Size+node[x].Cnt>=rk) {Splay(x);return node[x].Val;}//否则,如果当前节点左子树大小加上当前节点存在个数大于等于rk,说明当前元素就是答案,那么将它旋转到根节点,并返回答案
else rk-=node[node[x].Son[0]].Size+node[x].Cnt,x=node[x].Son[1];//否则,更新排名,并访问右子树
}
}
插入/查询操作还挺基础的,而删除操作就略显麻烦了。
首先,需要查询一下要删除元素的排名,目的是将这个元素旋到根。
然后分类讨论即可。
具体代码如下:
inline void Delete(int x)//删除一个值为x的元素
{
get_rank(x);//先通过查询,将它旋转到根
if(--node[rt].Cnt) return;//如果当前节点存在个数大于1,则将其存在个数减少1即可
if(!node[rt].Son[0]&&!node[rt].Son[1]) rt=0;//如果当前元素没有儿子,说明这棵Splay只有一个节点,将rt修改为0即可
else if(!node[rt].Son[1]) rt=node[rt].Son[0],node[rt].Father=0,PushUp(rt);//如果当前元素没有右儿子,那么直接将根修改为当前元素的左儿子即可
else if(!node[rt].Son[0]) rt=node[rt].Son[1],node[rt].Father=0,PushUp(rt);//类似的,如果当前元素没有左儿子,那么直接将根修改为当前元素的右儿子即可
else//否则,说明当前元素既有左儿子又有右儿子,那么就把当前元素的前驱作为新的根
{
int pre=node[rt].Son[0],k=rt;//用k来存储现在的根,用pre来求当前元素的前驱
while(node[pre].Son[1]) pre=node[pre].Son[1];//由于当前元素是根节点,所以左子树中最右边的一个节点就是当前元素的前驱
Splay(pre),node[node[k].Son[1]].Father=rt,node[rt].Son[1]=node[k].Son[1],PushUp(rt);//将这个前驱旋转至根,将原来的根的右儿子的父亲改为现在的根,再将现在的根的右儿子改为原来的根的右儿子,最后更新根节点的信息
}
}
最后,照常贴一份代码:
#include模板2:【洛谷3391】【模板】文艺平衡树
这个模板主要体现了 S p l a y Splay Splay的 维 护 区 间 翻 转 维护区间翻转 维护区间翻转的功能,而这也是 T r e a p Treap Treap和替罪羊树做不到的。
初始化时,我们用中序遍历到的顺序为 2 ∼ n + 1 2\sim n+1 2∼n+1的节点分别表示序列中第 1 ∼ n 1\sim n 1∼n个元素,并同时在一头一尾加入两个节点,防止越界。
然后,如果要翻转某个区间 [ l , r ] [l,r] [l,r],我们就找到这个区间的前后两个元素 l − 1 l-1 l−1和 r + 1 r+1 r+1,由于中序遍历到的顺序为 i + 1 i+1 i+1的节点表示序列中第 i i i个元素,也就是说我们要找到中序遍历到的顺序为 l l l和 r + 2 r+2 r+2的节点。
找到这两个节点后,我们将顺序为 l l l的节点旋转至根,并将顺序为 r + 2 r+2 r+2的节点旋转至根的右儿子。
我们可以发现,由于 B S T BST BST的性质,根的右儿子的左子树中每个节点被中序遍历到的顺序一定大于根节点且小于根节点的右子树,也就是说大于 l l l且小于 r + 2 r+2 r+2,在 [ l + 1 , r + 1 ] [l+1,r+1] [l+1,r+1]的范围内,而它们所表示的序列中的元素就是第 l ∼ r l\sim r l∼r个元素,因此,我们只需要给根的右儿子的左儿子打一个标记表示它被翻转了即可。
注意,在每次操作到一个节点时,必须先下推翻转标记,才能继续操作。
而下推操作很简单,只要交换左右儿子即可。
代码如下:
#include