HDU - 1542 Atlantis(线段树扫描线求矩形并的面积)
点我看题
题意:给出一系列的矩形的左下和右上点坐标,要求求出所有矩形并之后的面积和。
分析:这个分析可能有点儿长:)
这个题是扫描线的经典问题,确实是写了蛮久的,虽然以前也是A了的,但其实一直都没有搞透这个题,昨天想好好理一理这个思路,哇最后终于想通了。
首先
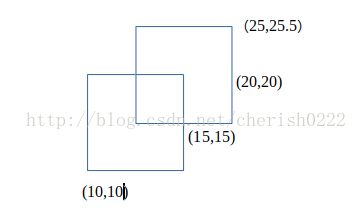
以这个矩形为栗子,这是我们要求的两个矩形的面积的并。
看到这个图,我们要怎么做呢?手算???对于这个题只有两个矩形手算当然很简单,但是如果有20个,200个,2000个……甚至更多的矩形呢?其实对于求矩形并后的面积和周长等类似问题,我们都可以用线段树的扫描线解决。
写到这里,我相信大家对线段树肯定都略知一二,但是扫描线是撒?
其实,扫描线就是我们假想的一根线,他可以从左向右(从右向左)或自下而上(自上而下)扫描这个组合后的图形,最后通过扫描操作得到自己想要的东西(这里得到的是横向线段的长度)。
现在具体来说说这题的解法。
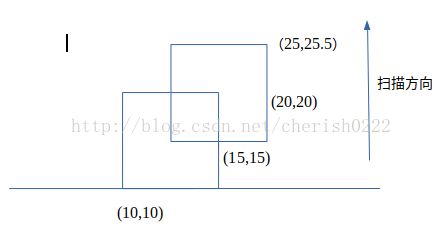
首先,我们想象一根扫描线自下而上扫描,如下
进行第一次扫描,可以得到下图蓝色的面积为S1。
继而进行第二次扫描,扫描线上移,得到下图绿色的面积为S2。
最后进行第三次扫描,得到黄色部分面积S3.
最后所得矩形并后的面积就是S1+S2+S3。
上面的还是比较好理解的,但是具体要如何用代码实现呢?
首先我们用一个结构体Edge来存每一条横向边,具体包括边的左右端点值,线段的高(纵坐标)以及一个标记(标记是矩形底边还是矩形上边)。
同时用一个数组x来离散化横坐标(本题横坐标为double型,不离散化无法建树)。
做好了上面的基础操作之后,我们就可以建树了。
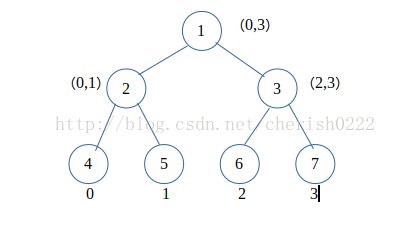
很重要的一点,我在下面建树的时候,叶子结点存的是一个区域,而不是一个点,就这个栗子来说,我的树是下面这个样子的
虽然结点4代表的是0,但其实它真正存的长度是x1-x0,同理,结点5存的是x2-x1,6存的是x3-x2……
这也就出现了线段树中的 int r = lower_bound(x,x+p,edge[i].r)-x-1;,r的位置之所以要减掉1,是因为这个点对应线段树的位置要减1,如果不能理解的话,可以自己手动跑一遍这个栗子,应该就能理解一二了。
线段树返回的是什么?返回的是扫描线扫描到的线段的长度。
得到长度之后,某一区域的面积就等于这个长度乘以之间的高度就好。
最后,这些小面积之后就是我们要求的总面积了。
哇哦哦,忘记说了,PushUp(rt)这个函数是用了更新线段的长度的,具体的可以看函数的注释。
参考代码:
/*线段树扫描线*/
/*从下往上扫描*/
#include
#include
#include
#include
#include
using namespace std;
#define lson rt<<1
#define rson rt<<1|1
const int maxn = 2e2+10;//最多只有100个点
int n;//矩形数
int e,p;//边数和点数
//边
struct Edge{
double l,r;//边的左右两点
double h;//边的高度
int tag;//边的标记,+1or-1,1代表下边,-1代表上边
};
Edge edge[maxn];
//线段树
struct SegTree{
int l,r;//线段树
int tag;//标记
double len;//长度
};
SegTree st[maxn<<2];
double x[maxn];//离散化之后的横坐标点
inline void GetEdge( double l, double r, double h, int tag)
{
edge[e].l = l;
edge[e].r = r;
edge[e].h = h;
edge[e].tag = tag;
e++;
}
inline void GetPoint( double xi)
{
x[p++] = xi;
}
//按照高度从小到大排序
bool cmp( Edge p, Edge q)
{
return p.h < q.h;
}
void Build( int l, int r, int rt)
{
st[rt].l = l;
st[rt].r = r;
st[rt].tag = st[rt].len = 0;
if( l == r)
return;
int mid = (l+r)>>1;
Build(l,mid,lson);
Build(mid+1,r,rson);
//本题不PushUp
}
void PushUp( int rt)
{
printf("tag=%d\n",st[rt].tag);
if( st[rt].tag)//tag>0,说明是下边,直接求出长度
st[rt].len = x[st[rt].r+1]-x[st[rt].l];
else if( st[rt].l == st[rt].r)//是个点,长度为0
st[rt].len = 0;
else//长度为儿子结点长度之和
st[rt].len = st[lson].len+st[rson].len;
}
void Update( int L, int R, int rt, int tag)
{
if( L <= st[rt].l && R >= st[rt].r)
{
st[rt].tag += tag;
PushUp(rt);
return;
}
int mid = (st[rt].l+st[rt].r)>>1;
if( R <= mid)
Update(L,R,lson,tag);
else if( L > mid)
Update(L,R,rson,tag);
else
{
Update(L,mid,lson,tag);
Update(mid+1,R,rson,tag);
}
PushUp(rt);
}
int main()
{
while( ~scanf("%d",&n) && n)
{
e = 0;
p = 0;
double x1,y1,x2,y2;
for( int i = 0; i < n; i++)
{
scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
GetEdge(x1,x2,y1,1);//底边
GetEdge(x1,x2,y2,-1);//定边
GetPoint(x1);//左端点
GetPoint(x2);//右端点
}
sort(edge,edge+e,cmp);
sort(x,x+p);
//点去重
int tmp = p;
p = 1;
for( int i = 1; i < tmp; i++)
if( x[i] != x[i-1])
x[p++] = x[i];
//建树
Build(0,p-1,1);
double ans = 0;
for( int i = 0; i < e-1; i++)
{
int l = lower_bound(x,x+p,edge[i].l)-x;
int r = lower_bound(x,x+p,edge[i].r)-x-1;
Update(l,r,1,edge[i].tag);
ans += (edge[i+1].h-edge[i].h)*st[1].len;
}
static int cas = 1;
printf("Test case #%d\n",cas++);
printf("Total explored area: %.2f\n\n",ans);
}
return 0;
}