用Python实现路径分类
用Python实现路径分类
目标
操场上有很多行人,从不同的入口进入,不同的路口出来,各自有不同的行走路径,现将这些行走轨迹分类,自行设计一个临界值,将相似的轨迹归为一类。
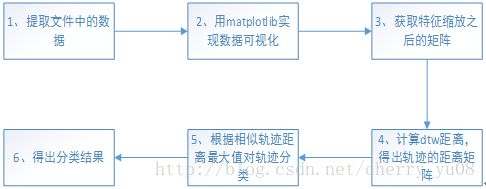
1、程序流程图
2、算法原理
①特征缩放
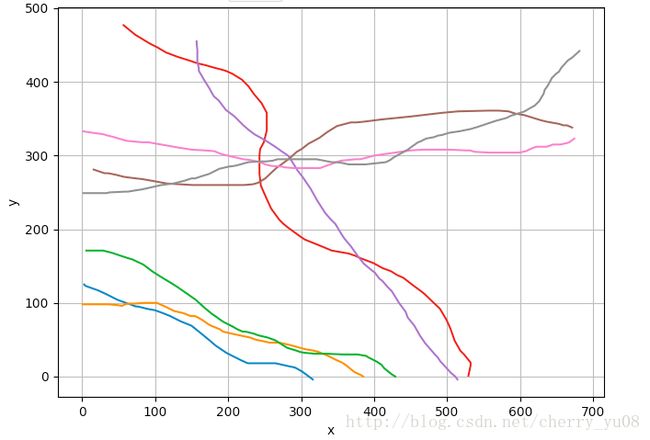
在本问题中,由于每条路径的起点不同、终点不同、路径长度不同,使用距离来计算相似度时会产生一定的误差,而采用特征缩放的方法,将坐标的值限定在(0,1)的区间中再计算距离,能有效减少误差,特征缩放公式为:坐标值/路径中的坐标最大值。
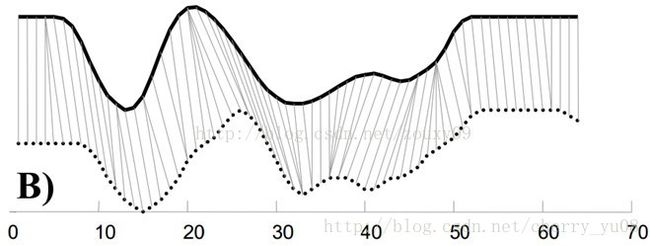
②DTW算法
由于每条路径的步数不同,即坐标数量不一致,那就不好直接计算点距之和作为两条路径的距离。DTW算法在计算两条路径距离时,可将其中一个(或者两个)序列在时间轴下warping扭曲,如下图所示,以达到更好的对齐,其中一条路径上的一点可对应于另一条路径上相似的几个点。DTW通过把时间序列进行延伸和缩短,来计算两个时间序列性之间的相似性,这一特性使得该算法可以很好地运用在本次的路径分类问题中。
3、 程序可调整的参数和说明
相似轨迹距离最大值为可调用的参数,它代表轨迹之间的距离,轨迹之间的距离是由上述DTW算法得出的,也可以理解为相似度。用户输入相似轨迹距离最大值后,程序依据该值对路径进行分类。
4、 程序的输入与输出
输入:相似轨迹距离的最大值;
输出:
a.数据集中的路径名和坐标数;
b.路径轨迹图;
c.路径总数;
d.相似度的最大值和最小值;
e.若干个分类以及每一类包含的路径;
5、程序运行截图
a. 如下图所示,进入代码文件所在的文件夹,用python命令运行程序;
![]()
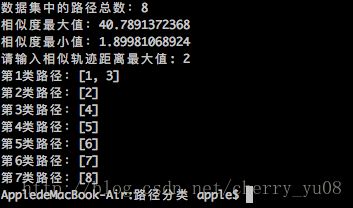
c. 如下图所示,关闭上面的路径图后,程序输出路径名、坐标数、路径总数、相似度等信息;

d.如下图所示,用户输入相似轨迹距离的最大值,程序根据该值计算出若干个分类,并显示每一个分类中包含的路径:
6、代码实现
import numpy as numpy
import matplotlib.pyplot as plt
'''
1、提取文件中的数据;2,用mayplotlib可视化数据;3、获取特征缩放之后的矩阵;
4、计算欧氏距离;5、使用dtw算法得出路径间的最小距离;
'''
#1、提取文件中的数据
def readFile(filename):
with open(filename, 'r') as f:
data = f.readlines() #txt中所有字符串读入data
#创建文件返回的矩阵
dataMatX = [] #创建一个空列表,存储X坐标
dataMatY = [] #创建一个空列表,存储Y坐标
for line in data:
line = line.strip() #去掉前后空格符或换行符
datax = [] #存放一组路径的x值
datay = [] #存放一组路径的y值
path = line.split(":") #以:分割
print("路径名:"+path[0]+"--坐标总数:"+path[1])
#这是路径坐标的部分
plot = path[2]
#遍历每组坐标
for i in plot:
everyPath = plot.split("#") #以#分割
#遍历每组路径
for i in range(len(everyPath)):
#veryPath[i]为二维数组,保存每一个轨迹的坐标
#以,符号为分隔符保存在p中
p = everyPath[i].split(",")
datax.append(int(p[0]))
datay.append(int(p[1]))
dataMatX.append(datax)
dataMatY.append(datay)
return dataMatX,dataMatY
#2、将文件中的数据可视化
def drawPath(datax,datay):
pathNum = len(datax)
for i in range(pathNum):
plt.plot(datax[i],datay[i],label = str(i+1))
#3、特征缩放,返回的值为0到1之间的矩阵
def featureScal(data):
for i in range(len(data)):
#将传进来list转化为数组
dataArray = numpy.array(data[i])
#获取每组数据的最大值
maxNum = numpy.max(dataArray)
#创建单位数组
b = numpy.ones(len(data[i]))
#初始化数组
for j in range(len(data[i])):
b[j] = maxNum
data[i] = dataArray/b
return data
#4、计算两点的欧氏距离
def calEuclideanDistance(dot1,dot2):
d1 = numpy.array(dot1)
d2 = numpy.array(dot2)
dist = numpy.sqrt(numpy.sum(numpy.square(d1 - d2)))
return dist
#5、计算得出两条路径之间的最小距离
def calDisMat(x1,x2,y1,y2):
#计算路径步数
n = numpy.size(x1)
m = numpy.size(x2)
#初始化距离矩阵
d = numpy.zeros([n,m])
for i in range(n):
for j in range(m):
d[i,j] = calEuclideanDistance([x1[i],y1[i]],[x2[j],y2[j]])
#累积距离矩阵
realmax = 1000
D = numpy.ones([n,m])*realmax
D[0,0] = d[0,0]
#动态规划
for i in range(1,n):
for j in range(m):
D1 = D[i-1,j]
if (j>=1):
D2 = D[i,j-1]
else:
D2 = realmax
if (i>=1 and j>=1):
D3 = D[i-1,j-1]
else:
D3 = realmax
D[i,j] = d[i,j] + numpy.min([D1,D2,D3])
#最小距离和
mindist = D[n-1,m-1]
return mindist
#6、根据相似矩阵进行分类,得出相似路径
def getPathClass(pathAlike):
#路径条数
lenMatrx = len(pathAlike)
#used表示某一路线是否已经被划分为某一类
used = []
#初始化used
for x in range(lenMatrx):
used.append(1)
#表示最后得到的路径路径
pathClass = []
#矩阵第i行
for i in range(lenMatrx):
#a2表示每一次遍历得到的相似路径
a2 = []
if (used[i] == 1): #等于1表示该路径还未被划分
a2.append(i)
used[i] = 0 #标记为被使用
#矩阵第j列
for j in range(i+1,lenMatrx):
#第i行j列为1
if (pathAlike[i,j] == 1):
if (j not in a2 and used[j] == 1):
a2.append(j)
used[j] = 0
for x in range(0,lenMatrx):
if (pathAlike[j,x] == 1): #与i行相关的第j列可看成第j行,找出与第j行相关的列
if (x not in a2 and used[x] == 1):
a2.append(x)
used[x] = 0 #标记为被使用
if (len(a2)): #判断a2是否为空
pathClass.append(a2)
for i in range(len(pathClass)):
pathClass[i] = [i+1 for i in pathClass[i]]
return pathClass
#----------------------------------------------------------------
#调用函数,获取文件中的数据,获取X坐标与Y坐标
X,Y = readFile("TrackData/TrackData-1.txt")
#可视化数据
plt.title('Path Lines')
plt.xlabel('x')
plt.ylabel('y')
#调用上面的绘图函数
drawPath(X,Y)
plt.legend(bbox_to_anchor=[0.3, 1])
plt.grid()
plt.show()
#调用函数进行特征缩放
fsDataMatX = featureScal(X)
fsDataMatY = featureScal(Y)
#计算路径之间的dtw距离,存放在矩阵中
pNum = len(fsDataMatX) #路径个数
maxLen = 0 #初始化距离最大值
minLen = 100 #初始化距离最小值
print("数据集中的路径总数:"+str(pNum))
#初始化相似矩阵,1表示相似,0不相似
pathAlike = numpy.zeros([pNum,pNum])
for i in range(pNum):
for j in range(pNum):
#计算dtw距离
pathDis = calDisMat(fsDataMatX[i],fsDataMatX[j],fsDataMatY[i],fsDataMatY[j])
if(maxLen < pathDis):
maxLen = pathDis
if(minLen > pathDis and pathDis != 0):
minLen = pathDis
print("相似度最大值:"+str(maxLen))
print("相似度最小值:"+str(minLen))
x = input("请输入相似轨迹距离最大值: ")
for i in range(pNum):
for j in range(pNum):
pathDis = calDisMat(fsDataMatX[i],fsDataMatX[j],fsDataMatY[i],fsDataMatY[j])
if(pathDis < float(x)):
pathAlike[i][j] = 1
#得出分类好的路径数组
pathClass = getPathClass(pathAlike)
for i in range(len(pathClass)):
print("第"+str(i+1)+"类路径:"+str(pathClass[i]))