一道网易笔试题（加入最优解法）

最近看完了表、栈、队列、二叉树、二叉搜索树、堆、Huffuman树的数据结构。突然想试试自己的程序水平有没有提高（似乎有点太急于求成^_^）。恰逢自己刚给网易投了一份简历，于是，在百度上搜了一些网易的笔试题。结果，其中这道题，一下把我难住了：

 

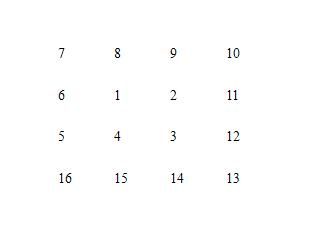
如图：

 

 

　

设“1”的坐标为（0，0） “7”的坐标为（－1，－1） 编写一个小程序，使程序做到输入坐标（X,Y）之后显示出相应的数字。

 

这个图有点像螺旋，它是按顺时针方向（由1->2->3->4->5…），逐渐向外膨胀。显然，如果以1为原点（0，0），以向右为x轴的正方向，以向下为y轴的正方向：

那么用人眼很容易就看出7的坐标为（－1，－1），这正与题目的假设一致。其他，如5的坐标应为（－1，1）。

但是，怎么让计算机知道呢？我的大脑突然不知所措，我在想，如果真出了这道题我挂定了^_^。但是，既然现在我是安然的坐在自己的卧室里，我绝对不会向它投降。

于是，躺在床上，望着天花板，想象着从这个螺旋的原点1出发，一起来看看：

Step1：从1向左走1步到达2。坐标（0，0）－>（1，0），即x加1。

Step2：从2向下走1步到达3，坐标（0，1）－>（1，1），即y加1。

Step3：从3向右走1步到达4，坐标（1，1）－>（0，1），即x减1。

Step4：从4向右走1步到达5，坐标（0，1）－>（－1，1），即x减1。

Step5：从5向上走1步到达6，坐标（－1，1）－>（－1，0），即y减1。

Step6：从6向上走1步到达7，坐标（－1，0）－>（－1，－1），即y减1。

……

当在大脑中想象着这一步一步的异同，一个灵感闪灵了。你是否发现了其中的规律？好吧，让我总结一下它的规律：

1、每向左(left)走一步，x就加1。每向右(right)走一步，x就减1。每向下(down)走一步，y就加1。每向上(up)走一步，y就减1。

这一条规律，只要有点直角坐标的知识，是显而易见的。当我们用程序去模拟这样一步一步地行走的时候，另外一个问题，就浮出水面了：怎样告诉计算机，让它按照一个顺时针的螺旋方式，去遍历每一个结点？比如，当计算机来到结点2的时候，它怎么知道，下一步应该往下走呢？当计算机来到结点5的时候，它怎么知道，下一点应该往上走呢？其实，这里还藏着另一条规律：

我把它叫做 状态转换的规律。这个规律包含两个方面：

2.1、从结点1开始，

A、向右走

B、向下走

C、向左走

D、向上走

又回到A。形成一个循环，即：A－>B－>C－>D－>A－>B……。

在每一个方向上，应该走多少步，才改变方向呢？现假设，现在开始改变方向，且已知上一次向右走了rNum步，向下走了dNum步，向左走了lNum步，向上走了uNum步。那么从现在开始，

2.2、沿新方向所走的步数，应该等于上一次相反方向所走的步数加1。例如，现在处于结点3，刚才从2－>3的时候是往下走，现在要改变方向，向左走了。这个时候，由于上一次向右走了1步（即由1－>2）。所以，这次应该向左走1＋1＝2步。

 

找到以上的两个规律，就可以写程序了。

我们可以用枚举类型，来标识四个方向（right,down,left,up）。

用四个整形变量，来记录上一次各个方向所走的步数（rNum,dNum,lNum,uNum）。

用四个整形变量，来记录在每一个方向累积所走的步数（rSum,dSum,lSum,uSum）。

这样，结点值就由这个公式确定：nodeVal = lSum+dSum+rSum+uSum+1。之所以加1，是因为原点的值为1，而不是0。

而坐标值可以这样确定：因为向右为x轴正方向，故x = rSum-lSum。因为向下为y轴的正方向，故y = dSum-uSum。

以下，是我用C++写的程序：

#include  < iostream >
#include  < conio.h >
using   namespace  std;

// 输入坐标，返回结点值
int  Val( int  x,  int  y)
{
     if  (x == 0   &&  y == 0 )
         return   1 ;
     // 四种行走方向
     enum  Order{right, down, left, up};
     // 上一次的行走的方向
     // 从状态循环思考，显然由1到2的上一步的状态应该是up。
    Order oState  =  up;    
    
     // 上一次 右、下、左、上移动的次数
     // 皆初始化为0
     int  rNum = 0 , dNum = 0 , lNum = 0 , uNum = 0 ;

     // 左、下、右、上累积移动的次数, 
     // 坐标满足：因为向右为x轴正方向，故x=rSum-lSum;
     // 因为向下为y轴正方向，故y=dSum-uSum;
     // 坐标所在结点的数值为：lSum+rSum+uSum+dSum+1;
     // 皆初始化为0
     int  lSum = 0 , dSum = 0 , rSum = 0 , uSum = 0 ;

     // 一个无限循环，一旦找到与x、y相等的坐标，则结束。
     while  ( true )
    {
         // 状态转换
         switch  (oState)
        {
         case  up:     // up->right        
            {
                rNum  =   0 ;
                 for  ( int  i = 0 ; i < lNum + 1 ; i ++ )
                {
                     ++ rNum;
                     ++ rSum;
                     if  (x  ==  rSum - lSum  &&  y  ==  dSum - uSum)
                         return  (lSum + rSum + uSum + dSum + 1 );

                }
                oState  =  right;
                 break ;
            }
         case  right:     // right->down
            {
                dNum  =   0 ;
                 for  ( int  i = 0 ; i < uNum + 1 ; i ++ )
                {
                     ++ dNum;
                     ++ dSum;
                     if  (x  ==  rSum - lSum  &&  y  ==  dSum - uSum)
                         return  (lSum + rSum + uSum + dSum + 1 );
                }
                oState  =  down;
                 break ;
            }
         case  down:     // down->left
            {
                lNum  =   0 ;
                 for  ( int  i = 0 ; i < rNum + 1 ; i ++ )
                {
                     ++ lNum;
                     ++ lSum;
                     if  (x  ==  rSum - lSum  &&  y  ==  dSum - uSum)
                         return  (lSum + rSum + uSum + dSum + 1 );
                }
                oState  =  left;
                 break ;
            }
         case  left:     // left->up
            {
                uNum  =   0 ;
                 for  ( int  i = 0 ; i < dNum + 1 ; i ++ )
                {
                     ++ uNum;
                     ++ uSum;
                     if  (x  ==  rSum - lSum  &&  y  ==  dSum - uSum)
                         return  (lSum + rSum + uSum + dSum + 1 );
                }
                oState  =  up;
                 break ;
            }
        }
    }    

}

int  main( int  argc, char   *  argv[])
{
     int  x, y;
    cout  << " 请输入坐标（x y）： " ;
     while  (cin >> x >> y)
    {
    cout  << " 坐标所在的结点值为： " <<  Val(x, y) << endl;
    cout  << " 请输入坐标（x y）： " ;
    }
     return   0 ;
}

  补充：此题最优秀的解法―――根据alula朋友的精彩回贴整理。能够根据规律挖掘出一个求解公式，就是最快速的方法。下面这个程序，做了充分的注释，只要在草稿上，按照注释，作一个图，就一目了然了：

#include  < iostream >
#include  < conio.h >
#include  < math.h >
using   namespace  std;

int  newVal( int  x,  int  y)
{
     // 以结点1为原点
     // 以相邻两结点间的距离为单位（如结点2与结点3的之间线段）
     // 结点7所在的正方形（由结点2、3、4、5、6、7、8、9构成）的边长
     // 的一半为1，即结点7到原点1的最大投影距离为1。
     // 于是由结点坐标，可以求出此结点所在的正方形的投影距离：
     int  r  =  max(abs(x),abs(y));    
    
     // 进行坐标变换，即把坐标原点移动到正方形的一个角结点上，
     // 使整个正方形落在第一象限，例如，当r=1时，将把坐标原点从结点1
     // 移动到结点7。
    x  +=  r;
    y  +=  r;

     // 正方形的边长，等于投影距离的两倍
     int  d  =   2 * r;

     int  s;     // s为结点在自己的正方形的偏移量
     if  (y  ==   0 )
        s  =   3 * d  +  x;
     else   if  (x  ==   0 )
        s  =   2 * d  +  (d - y);
     else   if  (y  ==  d)
        s  =  d  +  (d - x);
     else  
        s  =  y;

     // pow((r+1),2)为内层的结点数。
     // 例如，结点10的内层由结点1和正方形A（2、3、4、5、7、8、10）构成
     // 这些内层的总结点数恰为：(正方形A的边长＋1)的平方，
     // 因为：正方形A的边长 ＝（结点10所在正方形的半径－1）*2
     // 故：内层结点数 ＝ （结点10所在正方形的边长－1）的平方

   //结点值 ＝ 在当前正方形的偏移量 ＋ 内层的结点数
    s  +=  pow((d - 1 ), 2 );

     return  s;

}
int  main( int  argc, char   *  argv[])
{
     int  x, y;
    cout  << " 请输入坐标（x y）： " ;
     while  (cin >> x >> y)
    {
    cout  << " 坐标所在的结点值为： " << f(x, y) << endl;
    cout  << " 请输入坐标（x y）： " ;
    }
     return   0 ;
}