特征提取算法--Surf

本文参考了
http://blog.csdn.net/a784763307/article/details/17289251
http://blog.csdn.net/yujiflying/article/details/8203511
http://blog.csdn.net/cxp2205455256/article/details/41311013
SURF意指 加速的具有鲁棒性的特征，由Bay在2006年首次提出，这项技术可以应用于计算机视觉的物体识别以及3D重构中。SURF算子由SIFT算子改进而来，一般来说，标准的SURF算子比SIFT算子快好几倍，并且在多幅图片下具有更好的鲁棒性。SURF最大的特征在于采用了harr特征以及积分图像integral image的概念，这大大加快了程序的运行时间。
1. 构造高斯金字塔尺度空间
surf构造的金字塔图像与sift有很大不同，就是因为这些不同才加快了其检测的速度。Sift采用的是DOG图像，而surf采用的是Hessian矩阵行列式近似值图像。首先来看看图像中某个像素点的Hessian矩阵，如下：

即每一个像素点都可以求出一个Hessian矩阵。
H矩阵判别式为：

判别式的值是H矩阵的特征值，可以利用判定结果的符号将所有点分类，根据判别式取值正负，来判别该点是或不是极值点。在SURF算法中，用图像像素l(x，y)代替函数值f(x，y)，由于我们的特征点需要具备尺度无关性，所以在进行Hessian矩阵构造前，需要选用二阶标准高斯函数作为滤波器，经过滤波后在进行Hessian的计算，其公式如下：给定图像I中的一点X（x，y），在X点处，尺度为σ的Hessian矩阵H(x,σ)为

其中Lxx(x, σ)是高斯滤波后图像g(σ)的在x方向的二阶导数,其他的Lyy(x, σ)、Lxy(x, σ)都是g(σ)的二阶导数。
L（X，σ）= G（σ） x I（X）
L(X,σ)是一副图像在不同解析度下的表示，可以用高斯核G（σ）和图像函数I（X）在点X处的卷积实现，σ为高斯方差，这样就可以为图像中每个像素计算H行列式的特征值，并用这个值判别特征点。
一般计算图像的二阶导时，利用下面的公式d2f(x)/dx2=(f(x+1)-f(x))-(f(x)-f(x-1))=-2*f(x)+f(x+1)+f(x-1)。但是f(x)=g(h(x))【h(x)为图像的灰度值，f(x)是将h(x)高斯滤波处理的灰度函数。

最终我们要的是原图像的一个变换图像，因为我们要在这个变换图像上寻找特征点，然后将其位置反映射到原图中，在surf中，就是原图每个像素的Hessian矩阵行列式的近似值构成的。其行列式近似公式如下：

响应值还要根据滤波器大小进行归一化处理，以保证任意大小滤波器的F范数是统一的。0.9^2是滤波器响应的相关权重w是为了平衡Hessian行列式的表示式。这是为了保持高斯核与近似高斯核的一致性。

由于求Hessian时要先高斯平滑，然后求二阶导数，这在离散的像素点是用模板卷积形成的，这2种操作合在一起用一个模板代替就可以了，比如说y方向上的模板如下：

该图的左边即用高斯平滑然后在y方向上求二阶导数的模板，为了加快运算用了近似处理，其处理结果如右图所示，这样就简化了很多。并且右图可以采用积分图来运算，大大的加快了速度。
同理，x和y方向的二阶混合偏导模板如下所示：

积分图像，顾名思义，即指当前像素点所在位置距原点（0,0）所包围面的所有灰度之和。


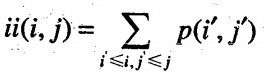
那么，当我们想要计算图片一个区域的积分，就只需计算这个区域的四个顶点在积分图像里的值，便可以通过2步加法和2步减法计算得出，其数学公式如下：

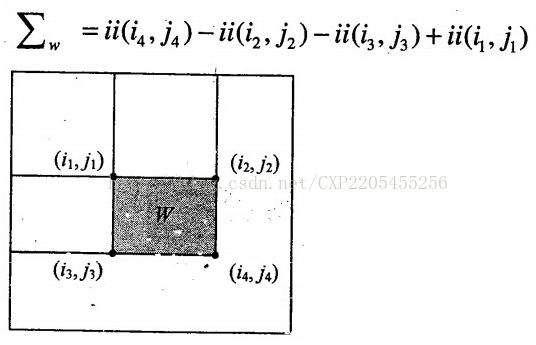
这样计算图像中任意一块矩形区域的灰度之和Sx只需要利用矩形4个顶点(Xi,Yi)(i=1,2,3,4 顺序为从上之下，先左后右)的积分值S（x,y）即可。
Sx=S(X1,Y1)+S(X4,Y4)-S(X2,Y2)-S(X3,Y3)
近似二阶导数的高斯模板并引入积分图像，只需要在函数定义之前计算各个坐标点的积分图像，然后就能方便的求出hessian的特征值。

上面讲的这么多只是得到了一张近似hessian行列式图，这好比sift中的DOG图，但是在金字塔图像中分为很多层，每一层叫做一个octave，每一个octave中又有几张尺度不同的图片。在sift算法中，同一个octave层中的图片尺寸(即大小)相同，但是尺度(即模糊程度)不同，而不同的octave层中的图片尺寸大小也不相同，因为它是由上一层图片降采样得到的。在进行高斯模糊时，sift的高斯模板大小是始终不变的，只是在不同的octave之间改变图片的大小。而在surf中，图片的大小是一直不变的，不同的octave层得到的待检测图片是改变高斯模糊尺寸大小得到的，当然了，同一个octave中的图片用到的高斯模板尺度也不同。
使用近似的Hessian矩阵行列式来表示图像中某一点x处的斑点响应值，遍历图像中所有的像元点，便形成了在某一尺度下斑点检测的响应图像。使用不同的模板尺寸，便形成了多尺度斑点响应的金字塔图像，利用这一金字塔图像，就可以进行斑点响应极值点的搜索。

右图是Surf的金字塔图。

2. 根据是否为邻域极大值判断特征点
这里要引入图像堆的概念，说简单点，就是一组大小相同的图像，这些图像都是根据不同大小高斯滤波二阶导模板， 得到的平滑后图像 。
所有小于预设极值的取值都被丢弃，增加极值使检测到的特征点数量减少，最终只有几个特征最强点会被检测出来。检测过程中使用与该尺度层图像解析度相对应大小的滤波器进行检测。
按照模板大小从小到大将平滑后图像沿z轴方向排布，这样中间层的每个像素点的领域就为3X3X3（包括上下两层）。若该点的特征值α为这27个点中的最大值，那么可以认为该点为Feature points–特征点（图像依据这些特征点的匹配进行更多的操作，比如拼接，比较相似性等等）。

和sift一样使用采用3维线性插值法得到亚像素级的特征点，同时也去掉那些值小于一定阈值的点。

3. 主方向确定
这一步与sift也大有不同。Sift选取特征点主方向是采用在特征点领域内统计其梯度直方图，取直方图bin值最大的以及超过最大bin值80%的那些方向做为特征点的主方向。而在surf中，不统计其梯度直方图，而是统计特征点领域内的harr小波特征。
为保证旋转不变性，首先以特征点为中心，计算半径为6s(S为特征点所在的尺度值)的邻域内的点在z、y方向的Haar小波(Haar小波边长取4s)响应，并给这些响应值赋高斯权重系数，使得靠近特征点的响应贡献大，而远离特征点的响应贡献小，其次将60度扇型范围内的响应相加以形成新的矢量，遍历整个圆形区域，选择最长矢量的方向为该特征点的主方向。这样，通过特征点逐个进行计算，得到每一个特征点的主方向。

4.构造surf特征点描述算子
在sift中，是在特征点周围取16*16的邻域，并把该领域化为4*4个的小区域，每个小区域统计8个方向梯度，最后得到4*4*8=128维的向量，该向量作为该点的sift描述子。
在surf中，首先将坐标轴旋转为关键点的方向，以确保旋转不变性。在特征点周围取一个正方形框，框的边长为20s(s是所检测到该特征点所在的尺度)。该框带方向，方向当然就是第4步检测出来的主方向了。然后把该框分为16个子区域，每个子区域统计25个像素的水平方向和垂直方向的haar小波特征，这里的水平和垂直方向都是相对主方向而言的。该haar小波特征为水平方向值之和，水平方向绝对值之和，垂直方向之和，垂直方向绝对值之和。该过程的示意图如下所示：

这样每个小区域就有4个值，所以每个特征点就是16*4=64维的向量，相比sift而言，少了一半，这在特征匹配过程中会大大加快匹配速度。

5. 采用最简单的两向量内积最大值为最匹配的点，设定一阈值，只有当这个最大值大于该阈值方可认为两特征点匹配。

这样Surf的算法知识大致就是这些，有一些部分我也没搞懂，就是积分图像计算Hessian矩阵的。