2018年第九届蓝桥杯省赛C/C++B组题解
“2018年第九届蓝桥杯省赛C/C++B组”题解目录:
1. 第几天
2. 明码
3. 乘积尾零
4. 测试次数
5. 快速排序
6. 递增三元组
7. 螺旋折线
8. 日志统计
9. 全球变暖
10. 乘积最大
1. 日期 答案:125
2000年的1月1日,是那一年的第1天。
那么,2000年的5月4日,是那一年的第几天?
方法一:表格下拉
方法二:java.util.Calendar 三行代码也可以搞定
2. 明码 答案: 9^9 = 387420489
汉字的字形存在于字库中,即便在今天,16点阵的字库也仍然使用广泛。
16点阵的字库把每个汉字看成是16x16个像素信息。并把这些信息记录在字节中。
一个字节可以存储8位信息,用32个字节就可以存一个汉字的字形了。
把每个字节转为2进制表示,1表示墨迹,0表示底色。每行2个字节,
一共16行,布局是:
第1字节,第2字节
第3字节,第4字节
....
第31字节, 第32字节
这道题目是给你一段多个汉字组成的信息,每个汉字用32个字节表示,这里给出了字节作为有符号整数的值。
题目的要求隐藏在这些信息中。你的任务是复原这些汉字的字形,从中看出题目的要求,并根据要求填写答案。
这段信息是(一共10个汉字):
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0
16 64 16 64 34 68 127 126 66 -124 67 4 66 4 66 -124 126 100 66 36 66 4 66 4 66 4 126 4 66 40 0 16
4 0 4 0 4 0 4 32 -1 -16 4 32 4 32 4 32 4 32 4 32 8 32 8 32 16 34 16 34 32 30 -64 0
0 -128 64 -128 48 -128 17 8 1 -4 2 8 8 80 16 64 32 64 -32 64 32 -96 32 -96 33 16 34 8 36 14 40 4
4 0 3 0 1 0 0 4 -1 -2 4 0 4 16 7 -8 4 16 4 16 4 16 8 16 8 16 16 16 32 -96 64 64
16 64 20 72 62 -4 73 32 5 16 1 0 63 -8 1 0 -1 -2 0 64 0 80 63 -8 8 64 4 64 1 64 0 -128
0 16 63 -8 1 0 1 0 1 0 1 4 -1 -2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 5 0 2 0
2 0 2 0 7 -16 8 32 24 64 37 -128 2 -128 12 -128 113 -4 2 8 12 16 18 32 33 -64 1 0 14 0 112 0
1 0 1 0 1 0 9 32 9 16 17 12 17 4 33 16 65 16 1 32 1 64 0 -128 1 0 2 0 12 0 112 0
0 0 0 0 7 -16 24 24 48 12 56 12 0 56 0 -32 0 -64 0 -128 0 0 0 0 1 -128 3 -64 1 -128 0 0
代码1:
#include
int number_bin[8], cnt = 0;
void print() {
for(int j=7; j>=0; j--) {
if(number_bin[j] != 0) printf("#");
else printf(" ");
}
}
void solve(int x) {
int len = 0;
for(int i=0; i<8; i++) {
number_bin[i] = x % 2; //或:x&1
x >>= 1; //非:x /= 2; // blog.csdn.net/qq_36949416/article/details/79784811
}
print();
cnt++;
if(cnt % 2 == 0) printf("\n");
}
int main() {
for(int i=0; i<10; i++) {
for(int j=0; j<32; j++) {
int x;
scanf("%d",&x);
solve(x);
}
}
return 0;
} 正整数的原码反码补码一样;负数的原码转反码:符号位不变,数值位按位取反。反码再转补码:末位加1。
#include
int number_bin[8], cnt = 0;
void print() {
for(int j=7; j>=0; j--) {
if(number_bin[j] != 0) printf("#");
else printf(" ");
}
}
void solve(int x) {
int flag = 0;
if(x < 0) {
number_bin[7] = 1;
x *= -1;
flag = 1;
}
int len = 0;
do{
number_bin[len++] = x % 2;
x /= 2;
} while(x != 0);
if(flag == 1) {
for(int i=0; i<7; i++) { //求反码
if(number_bin[i] == 1) number_bin[i] = 0;
else number_bin[i] = 1;
}
int y = 1;
for(int i=0; i<7; i++) { //求补码
number_bin[i] += y;
int temp = number_bin[i];
number_bin[i] %= 2;
y = temp / 2;
}
}
print();
cnt++;
if(cnt % 2 == 0) printf("\n");
for(int i=0; i<8; i++) {
number_bin[i] = 0;
}
}
int main() {
for(int i=0; i<10; i++) {
for(int j=0; j<32; j++) {
int x;
scanf("%d",&x);
solve(x);
}
}
return 0;
}
如下的10行数据,每行有10个整数,请你求出它们的乘积的末尾有多少个零?
5650 4542 3554 473 946 4114 3871 9073 90 4329
2758 7949 6113 5659 5245 7432 3051 4434 6704 3594
9937 1173 6866 3397 4759 7557 3070 2287 1453 9899
1486 5722 3135 1170 4014 5510 5120 729 2880 9019
2049 698 4582 4346 4427 646 9742 7340 1230 7683
5693 7015 6887 7381 4172 4341 2909 2027 7355 5649
6701 6645 1671 5978 2704 9926 295 3125 3878 6785
2066 4247 4800 1578 6652 4616 1113 6205 3264 2915
3966 5291 2904 1285 2193 1428 2265 8730 9436 7074
689 5510 8243 6114 337 4096 8199 7313 3685 211
方法一:统计因子2和5
#include
#include
#include
using namespace std;
int main() {
int cnt_2 = 0, cnt_5 = 0, n;
while(cin>>n) { //////ctrl+z +回车 结束输入
while(1) {
if(n % 2 == 0) {
n /= 2;
cnt_2++;
} else if(n % 5 == 0) {
n /= 5;
cnt_5++;
} else {
break;
}
}
}
printf("%d",min(cnt_2,cnt_5));
return 0;
} 方法二:手写大整数类... 用数组模拟高精度*低精度
#include
#include
using namespace std;
typedef long long ll;
ll d[10000], cnt1 = 0, cnt2;
void multi(ll x) {
cnt2 = 0;
if(cnt1 == 0) {
while(x != 0) {
d[cnt1++] = x % 10;
x /= 10;
}
} else {
ll carry = 0;
for(ll i=0; i=0; i--) {
printf("%lld",d[i]);
}
}
int main() {
ll x;
for(ll i=0; i<100; i++) {
scanf("%lld",&x);
multi(x);
}
print();
return 0;
} 方法三:打开 Java IDE ...
package code;
import java.util.*;
import java.math.*;
public class code1 {
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
BigInteger tempBig, sum = BigInteger.ONE;
while(cin.hasNext()) {
int temp = cin.nextInt();
tempBig = BigInteger.valueOf(temp);
sum = sum.multiply(tempBig);
}
System.out.println(sum);
}
}
//1121422219186536667024492011250763214808318968275
//064274407310238702780257290176056530569785046250819
//509674469344756137828597220816552935097142010674514
//916011440009400851737767517054438188613499916009689
//128296743684178986945081883648549881878817926137631
//614583656480718839220547362619409441203990312977268
//71056069331318210560000000000000000000000000000000
// 000 000 000 000 000 000 000 000 000 000 04. 测试次数 答案:19
x星球的居民脾气不太好,但好在他们生气的时候唯一的异常举动是:摔手机。各大厂商也就纷纷推出各种耐摔型手机。x星球的质监局规定了手机必须经过耐摔测试,并且评定出一个耐摔指数来,之后才允许上市流通。
x星球有很多高耸入云的高塔,刚好可以用来做耐摔测试。塔的每一层高度都是一样的,与地球上稍有不同的是,他们的第一层不是地面,而是相当于我们的2楼。
如果手机从第7层扔下去没摔坏,但第8层摔坏了,则手机耐摔指数=7。
特别地,如果手机从第1层扔下去就坏了,则耐摔指数=0。
如果到了塔的最高层第n层扔没摔坏,则耐摔指数=n
为了减少测试次数,从每个厂家抽样3部手机参加测试。
某次测试的塔高为1000层,如果我们总是采用最佳策略,在最坏的运气下最多需要测试多少次才能确定手机的耐摔指数呢?
请填写这个最多测试次数
DP:
假设dp[n][m]表示从n层楼m个手机找到的(在最坏情况下)摔手机不碎的最少判断次数。
假设一个手机从第i层扔下,那么有两种情况:
碎了,下面还有(i-1)层,剩下(m-1)个手机,需要dp[i-1,m-1]次。
没碎,上面还有(n-i)层,剩下m个手机,需要dp[n-i][m]次。(子问题)
有了子问题....那就动态规划:
状态转移方程:dp[n, m] = min{ 1 + max(dp[i - 1, m - 1], dp[n - i, m]) | i = 1..n }
边界: dp[i, 1] = i,dp[1, i] = 1
#include
#include
using namespace std;
int main() {
int high = 1000, phoneNum = 3, dp[1010][10];
//边界
for(int i=1; i<=high; i++) {
dp[i][1] = i;
}
for(int i=1; i<=phoneNum; i++) {
dp[1][i] = 1;
}
//状态转移方程
for(int i=2; i<=phoneNum; i++){
for(int j=2; j<=high; j++){
//从k=2层开始,找到k=2到j层取最小值
int minimal = 1000000000;
for(int k=2; k<=j; k++){
minimal = min(minimal, 1 + max(dp[k-1][i-1], dp[j-k][i]));
}
dp[j][i] = minimal;
}
}
//输出
printf("%d\n",dp[high][phoneNum]);
return 0;
} 5. 快速排序 答案:a, i+1, r, k-(i-l+1)
以下代码可以从数组a[]中找出第k小的元素。
它使用了类似快速排序中的分治算法,期望时间复杂度是O(N)的。
请仔细阅读分析源码,填写划线部分缺失的内容。
#include
int quick_select(int a[], int l, int r, int k) {
int p = rand() % (r - l + 1) + l;
int x = a[p];
{int t = a[p]; a[p] = a[r]; a[r] = t;}
int i = l, j = r;
while(i < j) {
while(i < j && a[i] < x) i++;
if(i < j) {
a[j] = a[i];
j--;
}
while(i < j && a[j] > x) j--;
if(i < j) {
a[i] = a[j];
i++;
}
}
a[i] = x;
p = i;
if(i - l + 1 == k) return a[i];
if(i - l + 1 < k) return quick_select( __________ ); //填空
else return quick_select(a, l, i - 1, k);
}
int main()
{
int a[] = {1, 4, 2, 8, 5, 7, 23, 58, 16, 27, 55, 13, 26, 24, 12};
printf("%d\n", quick_select(a, 0, 14, 5));
return 0;
}
6. 递增三元组
给定三个整数数组
A = [A1, A2, ... AN],
B = [B1, B2, ... BN],
C = [C1, C2, ... CN],
请你统计有多少个三元组(i, j, k) 满足:
1. 1 <= i, j, k <= N
2. Ai < Bj < Ck
【输入格式】
第一行包含一个整数N。
第二行包含N个整数A1, A2, ... AN。
第三行包含N个整数B1, B2, ... BN。
第四行包含N个整数C1, C2, ... CN。
对于30%的数据,1 <= N <= 100
对于60%的数据,1 <= N <= 1000
对于100%的数据,1 <= N <= 100000 0 <= Ai, Bi, Ci <= 100000
【输出格式】
一个整数表示答案
【样例输入】
3
1 1 1
2 2 2
3 3 3
【样例输出】
27
方法一:暴力三层循环
#include
int main() {
int n, a[80010], b[80010], c[80010], cnt = 0;
scanf("%d",&n);
int i, j, k;
for(i=0; i 方法二:分别排序, 然后枚举b数组的每个元素,然后查找a数组里面最后一个小于此元素的位置和c数组里面第一个大于此元素的位置。 得出了a中比此元素小的个数和b中比此元素大的个数,两两相乘,累加就是答案。
#include
#include
using namespace std;
const int MAXN = 100010;
int main() {
int n, a[MAXN], b[MAXN], c[MAXN], cnt = 0;
scanf("%d",&n);
int i, j, k;
for(i=0; i=0; i--) {
if(a[i] < b[j]) {
x = i + 1;
break;
}
}
for(k=0; k b[j]) {
y = n - k;
break;
}
}
cnt += x * y;
}
printf("%d\n",cnt);
return 0;
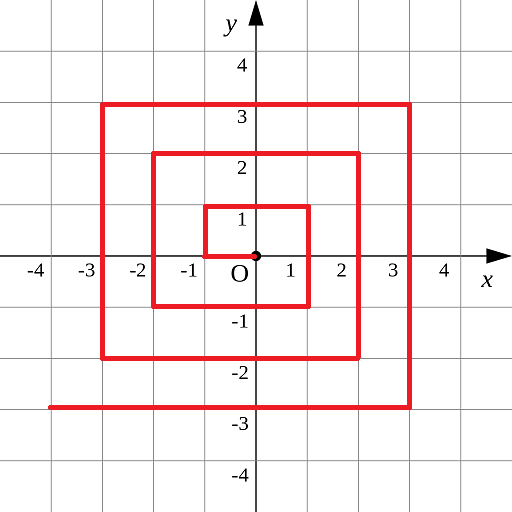
} 7. 螺旋折线
如图p1.png所示的螺旋折线经过平面上所有整点恰好一次。
对于整点(X, Y),我们定义它到原点的距离dis(X, Y)是从原点到(X, Y)的螺旋折线段的长度。
例如dis(0, 1)=3, dis(-2, -1)=9
给出整点坐标(X, Y),你能计算出dis(X, Y)吗?
【输入格式】
X和Y
对于40%的数据,-1000 <= X, Y <= 1000
对于70%的数据,-100000 <= X, Y <= 100000
对于100%的数据, -1000000000 <= X, Y <= 1000000000
【输出格式】
输出dis(X, Y)
【样例输入】
0 1
【样例输出】
3
#include
#include
#include
using namespace std;
typedef long long ll;
ll x, y, o;
ll solve() {
//计算基点的dis
ll dis = 3; //dis(0,1)
for(ll i=1; i= 0) { //第二象限
dis -= (abs(x) + abs(o - y));
} else if(x >= 0 && y > 0) { //一
dis += (abs(x) + abs(o - y));
} else if(x >= 0 && y <= 0) { //四
dis += (o * 2 + (abs(o - x) + abs(y)));
} else { //三
dis += (o * 2 * 2 + 1 + (abs(1 + x) + abs(o + y)));
}
return dis;
}
int main() {
scanf("%lld%lld",&x,&y);
if(x < -1 && y < 0) {
o = max(abs(x+1),abs(y)); //定位基点,各个基点为(0,1)(0,2)(0,3)...
} else {
o = max(abs(x),abs(y));
}
printf("%d\n",solve());
return 0;
} 8. 日志统计
小明维护着一个程序员论坛。现在他收集了一份"点赞"日志,日志共有N行。其中每一行的格式是:
ts id
表示在ts时刻编号id的帖子收到一个"赞"。
现在小明想统计有哪些帖子曾经是"热帖"。如果一个帖子曾在任意一个长度为D的时间段内收到不少于K个赞,小明就认为这个帖子曾是"热帖"。
具体来说,如果存在某个时刻T满足该帖在[T, T+D)这段时间内(注意是左闭右开区间)收到不少于K个赞,该帖就曾是"热帖"。
给定日志,请你帮助小明统计出所有曾是"热帖"的帖子编号。
【输入格式】
第一行包含三个整数N、D和K。
以下N行每行一条日志,包含两个整数ts和id。
对于50%的数据,1 <= K <= N <= 1000
对于100%的数据,1 <= K <= N <= 100000 0 <= ts <= 100000 0 <= id <= 100000
【输出格式】
按从小到大的顺序输出热帖id。每个id一行。
【输入样例】
7 10 2
0 1
0 10
10 10
10 1
9 1
100 3
100 3
【输出样例】
1
3
【输入样例】
7 10 2
0 1
0 10
10 10
11 1
1 1
100 3
100 3
【输出样例】
1
3
#include
#include 9. 全球变暖
你有一张某海域NxN像素的照片,"."表示海洋、"#"表示陆地,如下所示:
.......
.##....
.##....
....##.
..####.
...###.
.......
其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有2座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
.......
.......
.......
.......
....#..
.......
.......
计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
【输入格式】
第一行包含一个整数N。 (1 <= N <= 1000)
以下N行N列代表一张海域照片。
照片保证第1行、第1列、第N行、第N列的像素都是海洋。
【输出格式】
一个整数表示答案。
【输入样例】
7
.......
.##....
.##....
....##.
..####.
...###.
.......
【输出样例】
1
【输入样例】
10
..........
.##.......
.#..#.....
...###....
..###..#..
.....####.
.......#..
...#......
.###......
...#......
【输出样例】
2
【输入样例】
10
....................
..........
..........
..........
..#..#....
.######...
..#..#....
..........
..........
【输出样例】
0
#include
#include
using namespace std;
const int MAXN = 1010;
int n, pos[MAXN][MAXN], flag;
bool vis[MAXN][MAXN];
void DFS(int i, int j) {
if(pos[i][j] == flag && vis[i][j] == false) {
vis[i][j] = true;
DFS(i+1,j);
DFS(i-1,j);
DFS(i,j+1);
DFS(i,j-1);
}
}
int countNum() {
fill(vis[0],vis[0]+MAXN*MAXN,false);
int cnt = 0;
for(int i=0; i num1) {
printf("0\n"); //特判一个岛屿淹没完以后变成了两个岛屿
return 0;
}
printf("%d\n",num1 - num2);
return 0;
} ---------------------------------------- weiqv的分割线 -------------------------------------------
心态还是挺重要的... 急于做后面的且花了太多时间而然并卵,把前面的丢了... 还是怪自己太菜太菜太菜太菜太菜太菜... 开始得晚而且学习能力还底下... 而且还想得太多... MMP... 在时间还是在效率上付出得都不够