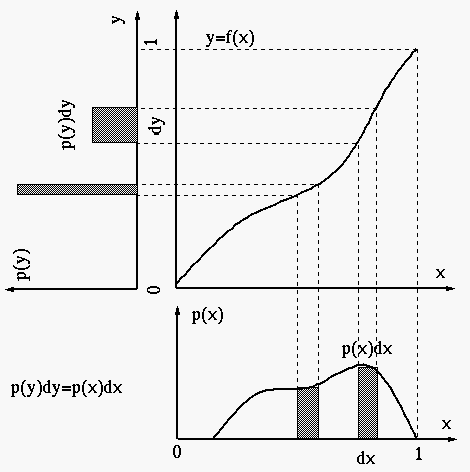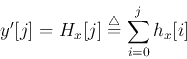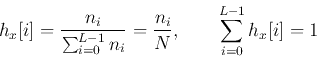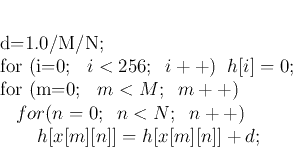直方图均衡算法
直方图均衡的原因
大多的图像的灰度分布集中在较窄的区间,利用直方图均衡可以将对对比图进行调整,增强局部的对比度,特别在图像有用对比度相当接近的情况,直方图均衡可以很好的增强对比度使得图像的细节更清晰,达到图像增强的目的。
图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。直方图拉伸是通过对比度拉伸对直方图进行调整,从而“扩大”前景和背景灰度的差别,以达到增强对比度的目的,这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。
直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。
缺点:1)变换后图像的灰度级减少,某些细节消失;
2)某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
1. 灰度级直方图
它反应一副图中的灰度级与此灰度级的概率间的图形。假设r为灰度级,则相应的概率为p(r)。表示相应的灰度级r出现的概率。该函数的图形则称为这幅图像的直方图。
直方图均衡化的作用是图像增强。
有两个问题比较难懂,一是为什么要选用累积分布函数,二是为什么使用累积分布函数处理后像素值会均匀分布。
第一个问题。均衡化过程中,必须要保证两个条件:①像素无论怎么映射,一定要保证原来的大小关系不变,较亮的区域,依旧是较亮的,较暗依旧暗,只是对比度增大,绝对不能明暗颠倒;②如果是八位图像,那么像素映射函数的值域应在0和255之间的,不能越界。综合以上两个条件,累积分布函数是个好的选择,因为累积分布函数是单调增函数(控制大小关系),并且值域是0到1(控制越界问题),所以直方图均衡化中使用的是累积分布函数。
第二个问题。累积分布函数具有一些好的性质,那么如何运用累积分布函数使得直方图均衡化?比较概率分布函数和累积分布函数,前者的二维图像是参差不齐的,后者是单调递增的。直方图均衡化过程中,映射方法是
其中,n是图像中像素的总和,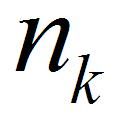 是当前灰度级的像素个数,L是图像中可能的灰度级总数。
是当前灰度级的像素个数,L是图像中可能的灰度级总数。
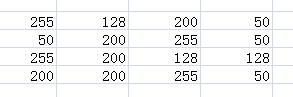
来看看通过上述公式怎样实现的拉伸。假设有如下图像:
得图像的统计信息如下图所示,并根据统计信息完成灰度值映射:
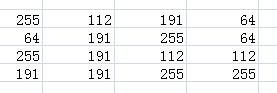
映射后的图像如下所示:
以上就是直方图映射均衡化的步骤,当然还有一些基于此的更优算法,比如Photoshop中的方法,在此就不一一列举了,大同小异。
参考:
http://blog.csdn.net/zrongh/article/details/7302816 直方图均衡化原理
http://bbs.ednchina.com/BLOG_ARTICLE_219471.HTM 直方图均衡化
直方图均衡化是灰度变换的一个重要应用,它高效且易于实现,广泛应用于图像增强处理中。图像的像素灰度变化是随机的,直方图的图形高低不齐,直方图均衡化就是用一定的算法使直方图大致平和。
均衡化处理后的图象只能是近似均匀分布。均衡化图象的动态范围扩大了,但其本质是扩大了量化间隔,而量化级别反而减少了,因此,原来灰度不同的象素经处理后可能变的相同,形成了一片的相同灰度的区域,各区域之间有明显的边界,从而出现了伪轮廓。
如果原始图像对比度本来就很高,如果再均衡化则灰度调和,对比度降低。在泛白缓和的图像中,均衡化会合并一些象素灰度,从而增大对比度。均衡化后的图片如果再对其均衡化,则图像不会有任何变化。
灰度直方图均衡化的算法,简单地说,就是把直方图的每个灰度级进行归一化处理,求每种灰度的累积分布,得到一个映射的灰度映射表,然后根据相应的灰度值来修正原图中的每个像素。
经典的直方图均衡化算法可能存在以下一些不足:
- 输出图像的实际灰度变化范围很难达到图像格式所允许的最大灰度变化范围。
- 输出图像的灰度分布直方图虽然接近均匀分布, 但其值与理想值1/n仍有可能存在较大的差异, 并非是最佳值。
- 输出图像的灰度级有可能被过多地合并。由于灰度的吞噬也易造成图像信息的丢失。
为此人们提出了许多改进的直方图均衡算法,详细内容请参阅本文末尾提供的参考资料。
公式
要写论文的同学可能需要用数学的方式来描述,下面我把前面讲的内容概括成公式,以供参考。
概率密度函数(PDF)
为了计算方便,我们需要将直方图归一化,即把灰度范围由0~255变为0~1。归一化后的直方图其实就是一个概率密度函数(PDF,probability density function),均衡化就是令概率密度为1。
我们用Pr(r)来表示原图像的PDF,用Ps(s)表示均衡化之后的PDF,r、s分别代表均衡化前后的灰度值,r,s∈[0,1]。根据概率论的知识,可得出:
公式中,T(rk)来表示原图像的第k个灰度级的转换函数。∑表示总和。∑nj/N表示0~j个灰度级的像素数量总和与像素总数的比值,也就是前面讲过的百分位(当前色阶与前面色阶的所有像素数量÷总像素数量)。∑Pr(rk)表示第0~k的灰度级出现概率累积相加。因为s是归一化的数值(s∈[0,1]),要转换为0~255的颜色值,需要再乘上255,即S=∑Pr(rk)*255。
这个转换公式也被称为图像的累积分布函数
(CDF,cumulative distribution function)。
彩色算法
彩色的直方图均衡化其实就是对图像某个或多个颜色通道进行灰度直方图均衡化运算,常见的有以下几种方法:
统计所有RGB颜色通道的直方图的数据并做均衡化运算,然后根据均衡化所得的映射表分别替换R、G、B通道颜色值。
分别统计R、G、B颜色通道的直方图的数据并做均衡化运算,然后根据R、G、B的映射表分别替换R、G、B通道颜色值。
用亮度公式或求RGB的平均值的方式计算亮度通道,然后统计亮度通道的直方图的数据并做均衡化运算,然后根据映射表分别替换R、G、B通道颜色值。
直方图均衡化
直方图均衡化是对图像的灰阶进行变换,使变换后图像的直方图成为常量值:
目的:
l 均衡利用动态范围内的所有灰阶;
l 进一步做直方图规定(histogram specification)用.
我们首先假设![]() 范围内的灰度值是连续的,映射函数
范围内的灰度值是连续的,映射函数![]() 将x映射到同样取值范围内的y。我们再假设输入图像中
将x映射到同样取值范围内的y。我们再假设输入图像中![]() 区间内的灰度值被映射到输出图像的
区间内的灰度值被映射到输出图像的![]() 区间。由于映射前后的像素个数不变,所以有:
区间。由于映射前后的像素个数不变,所以有:
因为输出图像的直方图被均衡化了,其值应为1,即![]() ,所以有
,所以有![]() ,于是可以得到:
,于是可以得到:
对两边求积分,我们就可以从直方图均衡化中获得映射函数:
直方图均衡化可以直观的理解如下:
l 如果![]() 值较大,那么
值较大,那么![]() 就会比较陡峭,
就会比较陡峭,![]() 就会比较宽,为了满足
就会比较宽,为了满足![]() ,会导致
,会导致![]() 值比较小;
值比较小;
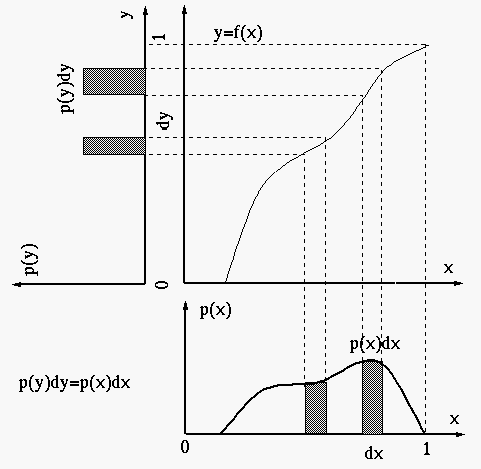
l 如果![]() 值较小,那么
值较小,那么![]() 就会比较平缓,
就会比较平缓,![]() 就会比较窄,会导致
就会比较窄,会导致![]() 值比较大。
值比较大。
当灰阶值为离散值时,输入灰阶x为![]() 范围内的一个离散值,此时连续的映射函数变为离散:
范围内的一个离散值,此时连续的映射函数变为离散:
其中![]() 为灰阶值为i的像素个数,N为总像素个数。
为灰阶值为i的像素个数,N为总像素个数。
其中![]() 是小于实数
是小于实数![]() 的最大整数值,加上0.5是为更准确地取整。注意,两种方法中都是将
的最大整数值,加上0.5是为更准确地取整。注意,两种方法中都是将![]() 映射到最高灰阶值
映射到最高灰阶值![]() ,而第二种变换中还
,而第二种变换中还![]() 将映射到0而使输出图像的灰阶值占据整个动态范围,第二种变换同时做了灰度值范围拉伸和直方图均衡。
将映射到0而使输出图像的灰阶值占据整个动态范围,第二种变换同时做了灰度值范围拉伸和直方图均衡。
例子:
假设图像大小为![]() ,灰阶个数为
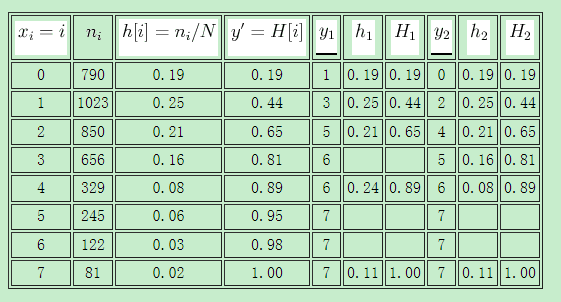
,灰阶个数为![]() ,下表显示了以上两种变换方法下的直方图均衡化过程:
,下表显示了以上两种变换方法下的直方图均衡化过程:
上面的例子表明给定图像的直方图被均衡化了。虽然均衡化的直方图看起来并不是一个常量值,但是其累计分布直方图是一条严格上升的斜线表明直方图确实被均衡化了。均衡化的直方图不能保证是一个常量值是由于同一个灰阶值的像素没有办法再被分开成多个灰阶的像素来保证达到均值分布。
编程问题:
l 获取输入图像的直方图:
l 构建查找表:
l 图像映射:
例子:
原文:http://fourier.eng.hmc.edu/e161/lectures/contrast_transform/node2.html