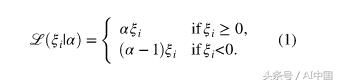从线性模型到决策树再到深度学习的分位数回归

假设房地产分析师想要根据家庭、年龄以及就业中心的距离来预测房价。其典型的目标是在给定这些因素的情况下生成最佳房价点估计，其中"最佳"通常是指预测与现实之间的最小平方偏差。

但是，如果他们想要预测的不只是单一的估计，还有其范围呢？这称为预测区间，产生它们的一般方法称为分位数回归。在这篇文章中，我将描述这个问题是如何正式化，如何采用六种线性，基于决策树和深度学习的方法中实现它（在Python中，这是Jupyter记事本），以及它们如何针对真实数据集执行的。

https://colab.research.google.com/drive/1nXOlrmVHqCHiixqiMF6H8LSciz583_W2

分位数回归的最小化分位数损失

正如回归最小化平方误差损失函数以预测单点估计一样，分位数回归最小化了预测某个分位数时的分位数损失。最流行的分位数是中位数或第50%，在这种情况下，分位数损失只是绝对误差的总和。其他分位数可以给出预测区间的终点。例如，中间80％的范围由第10%和90%来定义。分位数损失根据评估的分位数而不同，使得更多的负误差对于更高的分位数更多地受到惩罚，并且更多的正误差对于更低的分位数更加不利。

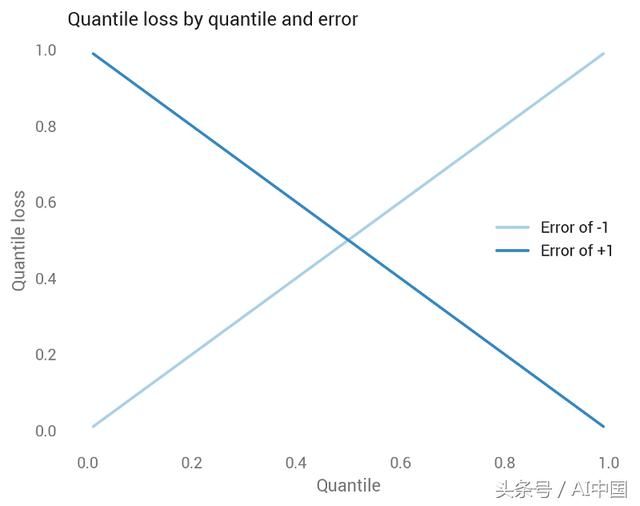
在深入研究公式之前，假设我们已经预测了一个真值为零的单点，我们的预测范围从-1到+1。也就是说，我们的错误范围从-1到+1。该图表示分位数损失如何随误差而变化，具体取决于分位数。  

让我们分别看每一行：

• 中蓝色线显示中位数，它在零附近对称，其中所有损失均等于零，因为预测是完美的。到目前为止看起来很好：中位数的目的是将预测集合平分，因此我们希望将低估等同于高估。正如我们很快就会看到的那样，中位数附近的分位数损失是绝对偏差的一半，因此-1和-1都是0.5，0时是0。

• 浅蓝色线显示第10个百分位数，它为负误差分配较低的损失，对正误差分配较高的损失。第10个百分位意味着我们认为真实价值低于该预测值的可能性为10％，因此将低估的损失分配给低估，而不是高估是有意义的。

• 深蓝色线显示第90个百分位数，这是与第10个百分位数相反的模式。我们还可以通过分位数来查看低估和高估的预测。分位数越高，分位数损失函数惩罚低估的次数就越多，惩罚高估的次数就越少。  

鉴于这种直觉，这里是分位数损失公式：

在Python代码中，我们可以用最大语句替换分支逻辑：

接下来我们将看看六种方法：最小二乘法（OLS）、线性分位数回归、随机森林、梯度提升、Keras和TensorFlow，并了解它们如何与一些真实数据一起工作。

数据

该分析将使用波士顿住房数据集，其中包含代表波士顿地区城镇的506个观测值。它包括目标旁边的13个特征，自住房屋的中位值。因此，分位数回归预测城镇（非住宅）的比例，其中位值住宅价值低于一个值。

https://www.kaggle.com/c/boston-housing

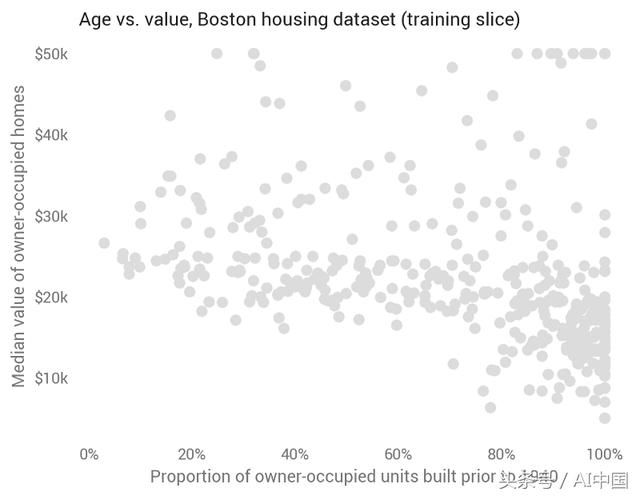
我训练80％的模型并测试剩余的20％。为了便于可视化，第一组模型使用单一特征：AGE，即1940年之前建造的住户自用单位的比例。正如我们所预期的那样，城镇的较旧房屋拥有较低的价值，尽管这种关系是嘈杂的。

对于每种方法，我们将预测测试集上的第10个，第30个，第50个，第70个和第90个百分位数。

（1）普通最小二乘法（OLS）

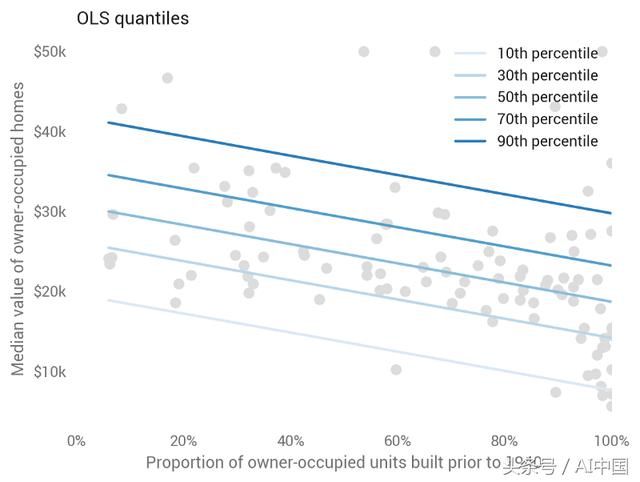
虽然最小二乘法（OLS）预测均值而不是中值，但我们仍然可以根据标准误差和逆正态累积分布函数（CDF）计算预测区间：

这种基线方法产生以均值为中心的线性和平行分位数（预测为中位数）。经过良好调整的模型将在顶部和底部线之间显示大约80％的点。请注意，这些点与第一个散点图不同，因为我们在此处显示了用于评估样本外预测的测试集。

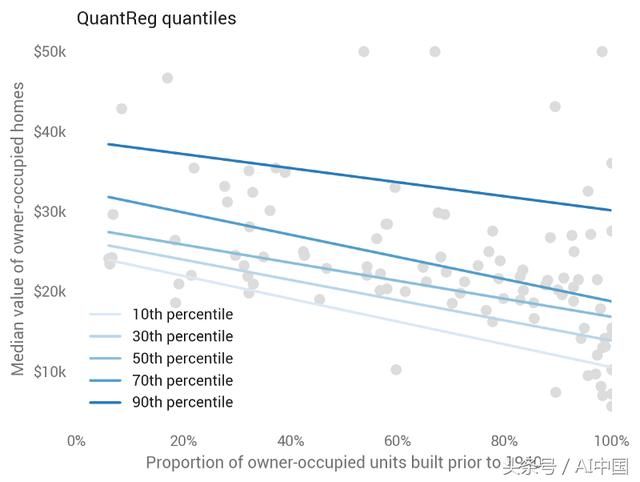
（2）线性分位数回归

线性模型超出平均值到中位数和其他分位数。线性分位数回归预测给定的分位数，放松最小二乘法的平行趋势假设，同时仍然强加线性（它使分位数损失最小化）。这对于statsmodel来说很简单：

（3）随机森林

我们首次离开线性模型的是决策树的一种集合随机森林。虽然这个模型没有明确地预测分位数，但我们可以将每棵树视为一个可能的值，并使用其经验CDF计算分位数：

https://blog.datadive.net/prediction-intervals-for-random-forests/

在这种情况下，它有点疯狂，暗示过度拟合。由于随机森林更加常用于高维数据集，我们将在向模型添加更多功能后返回它们。  

（4）梯度提升

另一种基于决策树的方法是梯度提升，scikit-learn的实现支持显式分位数预测：ensemble.GradientBoostingRegressor（loss ='quantile'，alpha = q）

http://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html

虽然不像随机森林那样跳跃，但它在单一特征模型上看起来并不好看。  

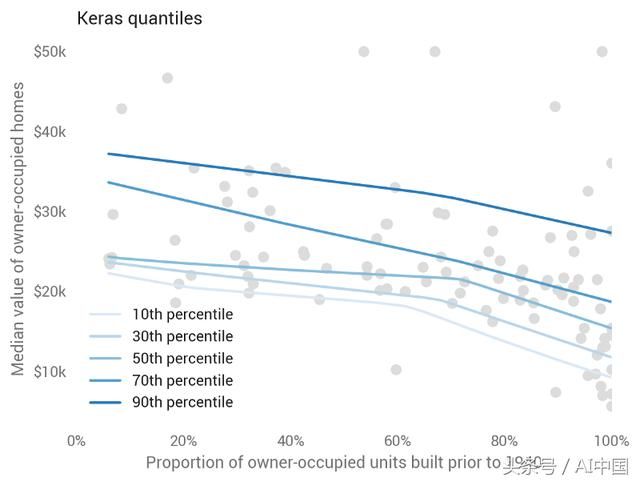
（5）Keras（深度学习）

Keras是一个用户友好的包装器，包括TensorFlow的神经网络工具包。因此需要查看Jupyter记事本或阅读Sachin Abeywardana的更多信息，了解它是如何工作的。https://colab.research.google.com/drive/1nXOlrmVHqCHiixqiMF6H8LSciz583_W2#scrollTo=g7s7Grj-A-Sf

最底层的网络是具有扭结的线性模型（称为整流线性单元，或ReLU），我们可以在视觉上看到：Keras预测在1940年之前建造的城镇住宅价值会增加70％，同时在非常低和非常高的房龄。这似乎是基于测试数据拟合的良好预测。  

（6）TensorFlow

Keras的一个缺点是必须分别训练每个分位数。为了利用分位数共有的模式，我们必须转到TensorFlow本身。请参阅Jupyter笔记本和Jacob Zweig的笔记本以了解更多相关信息。

https://colab.research.google.com/drive/1nXOlrmVHqCHiixqiMF6H8LSciz583_W2#scrollTo=g7s7Grj-A-Sf

我们可以在其预测中看到跨越分位数的这种共同学习，其中模型学习共同的扭结而不是每个分位数的单独的扭结。这看起来是一个很好的奥卡姆风格的选择。  

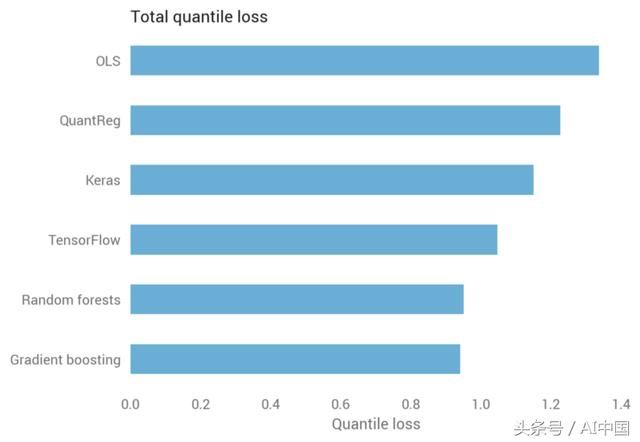
哪个做得最好？

通过观察表明深度学习表现良好，线性模型表现良好，基于决策树的方法表现不佳，但我们能否量化哪个最好？是的，我们可以使用测试集上的分位数损失。

回想一下，分位数损失根据分位数而不同。由于我们计算了五个分位数，因此测试集中的每个观测值都有五个分位数损失。对所有分位数观测值求平均证实了视觉直觉：随机森林的表现最差，而TensorFlow表现最佳。  

我们也可以通过分位数来解决这个问题，揭示基于决策树的方法在第90百分位时表现得特别差，而深度学习在较低的分位数处表现最佳。  

较大的数据集提供了更多改进最小二乘法（OLS）的机会

因此，随机森林对于这个单一特征的数据集非常糟糕，但这并不是它们的目的。如果我们将其他12个功能添加到波士顿的住宅模型会发生什么？  

基于决策树的方法卷土重来，最小二乘法（OLS）在改进后，将与其他非决策树方法之间的差距不断扩大。

现实世界的问题往往超出预测手段。也许应用程序开发人员不仅对用户的预期用途感兴趣，而且对他们成为超级用户的可能性感兴趣。或者一家汽车保险公司想知道司机在不同门槛下的高价值索赔的可能性。经济学家可能希望随机将信息从一个数据集归结于另一个数据集，从CDF中挑选以确保适当的变化（我将在后续文章中探讨一个例子）。

分位数回归对于这些用例中的每一个都很有价值，并且机器学习工具通常可以胜过线性模型，尤其是易于使用的基于树的方法。那么尝试采用自己的数据，让我知道它是怎么回事！

来自 “ ITPUB博客 ” ，链接：http://blog.itpub.net/31545819/viewspace-2217710/，如需转载，请注明出处，否则将追究法律责任。

转载于:http://blog.itpub.net/31545819/viewspace-2217710/