Meta Path 定义
原文地址:
https://blog.csdn.net/hy_jz/article/details/78862226
Meta Path 是2011年 Yizhou Sun etc. 提出的 http://www.morganclaypool.com/doi/abs/10.2200/S00433ED1V01Y201207DMK005, 针对异质网络中的相似性搜索。
Meta Path 是一条包含relation序列的路径,而这些 relation 定义在不同类型object之间。
- Information Network
信息网络是指一个有向图 G=(V,E), 同时还有一个object类型映射函数 ϕ:V→Aϕ:V→A,边类型映射函数ψ:E→Rψ:E→R。每一个object v∈Vv∈V, 都有一个特定的object 类型ϕ(v)∈Aϕ(v)∈A;每一条边 e∈Ee∈E 都有一个特定的relation ψ(e)∈Rψ(e)∈R。
异质网络(Heterogeneous Network)指的是object的类型|A|>1|A|>1或者relation的类型|R>1||R>1|。 - Network Schema
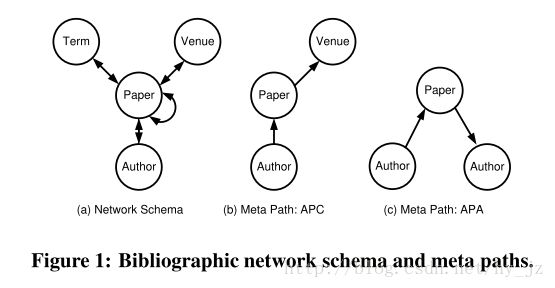
Network schema,定义为:TG=(A,R)TG=(A,R),是信息网络 G=(V, E)的一种 meta模板,这个信息网络有一个object类型映射函数 ϕ:V→Aϕ:V→A 和 link 类型映射函数ψ:E→Rψ:E→R。信息网络G是一个定义在object类型AA上的有向图,并且边是RR中的relation。
- Meta-Path
Meta Path PP定义在 network schema TG=(A,R)TG=(A,R)上,具体形式为A1⟶R1A2⟶R2⋯⟶RlAl+1A1⟶R1A2⟶R2⋯⟶RlAl+1
这其实是在节点类型A1,Al+1A1,Al+1之间定义了一个组合关系R=R1∘R2∘⋯∘RlR=R1∘R2∘⋯∘Rl。∘∘代表着relation之间的组合操作。
如果在v1,vl+1v1,vl+1之间的路径 p=(v1,v2,⋯,vl+1)p=(v1,v2,⋯,vl+1)服从metapath PP,那么它必须满足 ∀i,ϕ(vi)=Ai∀i,ϕ(vi)=Ai,并且每一个link ei=
meta-path PP的返定义为 P−1P−1。
两个meta-path P1=(A1,A2,⋯,Al)P1=(A1,A2,⋯,Al) 和 P2=(A′1,A′2,⋯,A′k)P2=(A1′,A2′,⋯,Ak′)可以拼接,当且仅当 Al=A′1Al=A1′。拼接后的路径是P=(P1,P2)P=(P1,P2),等价(A1,A2,⋯,Al,A′2,⋯,A′k)(A1,A2,⋯,Al,A2′,⋯,Ak′)
-
给定一个用户指定的meta-path P=(A1,A2,⋯,Al)P=(A1,A2,⋯,Al), 那么在节点对 x∈A1,y∈Alx∈A1,y∈Al 上,根据他们之间符合PP的路径实例,可以定义几个相似性指标:
- Path Count:在节点x,节点y之间符合meta-path PP的路径实例p的数目:s(x,y)=|p:p∈P|s(x,y)=|p:p∈P|。
- Random Walk: s(x,y)是从x节点开始,到y节点结束,服从PP的random walk概率。s(x,y)=∑p∈PProb(p)s(x,y)=∑p∈PProb(p)。
- Pairwise Random Walk: 一个meta-path PP 可以被分解为两个较短的但是等长的路径 P=(P1P2)P=(P1P2), 那么s(x,y)就是从x,y开始到达相同的中间节点的 节点对随机游走 概率。s(x,y)=∑(p1p2)∈(P1P2)Prob(p1)Prob(p−12)s(x,y)=∑(p1p2)∈(P1P2)Prob(p1)Prob(p2−1),其中 Prob(p1)Prob(p1) 和 Prob(p−12)Prob(p2−1)是两条路径实例的随机游走概率。
-
PahtSim 相似性度量
Path Count 和基于Random Walk 的相似性总是倾向于度大的节点;而Pairwise Random Walk 相似性倾向于集中的(concentrated)节点,即:大多数link连接到一小部分节点。对于PathSim,两个节点相似不仅仅是直接相连的节点,也共享可比的可视性(comparable visibility)。由于对等(peer)关系应该是对称的,因此我们将PathSim 简称为对称元路径。s(x,y)=2×|{px⇝y:px⇝y∈P}||{px⇝x:px⇝x∈P}|+|{py⇝y:py⇝y∈P}|
--------------------- 作者:hy_jz 来源:CSDN 原文:https://blog.csdn.net/hy_jz/article/details/78862226?utm_source=copy 版权声明:本文为博主原创文章,转载请附上博文链接!