通过例子讲解回溯法、分枝限界法

1.写在前面

        这学期上算法课，对分枝限界法这一章听的似懂非懂。后来复习备考时，参考了王晓东老师的《计算机算法设计与分析》，把这部分的原理彻底整明白了，在此与大家分析心得。我将结合自己的理解和书上的几个例子，来具体说明回溯法和分枝限界法原理，实现代码网上比比皆是，故不再赘述。

        算法整体而言，大致可以分为3类，基于规模、基于搜索、随机化。基于规模的算法主要有分治、动态规划、贪心算法；基于搜索的有回溯和分枝限界法；随机化严格来说是一种策略，能优化算法的性能，主要有舍伍德算法、拉斯维加斯算法和蒙特卡洛。以上是“算法设计与分析”这门课的体系，分枝限界法是基于搜索的一种算法，下面也会通过实例和回溯法进行对比，以说明二者的区别和联系。

2.例子一(0-1背包问题)

        对于n=3的0-1背包问题，考虑以下实例：3个商品的重量weight=[16, 15, 15]，对应的价值为value=[45, 25, 25]，背包允许装入的总重量为c=30，优化目标是在背包中装入商品的重量不超过c的情况下，最大化装入商品的价值。

        先不考虑背包重量的限制c，则每个商品有选择装入和不装两种可能，所以一共有2^3=8种选择，即{(0, 0, 0), (0, 0, 1), …… ,(1, 1, 1)}。大括号{}整体称为解空间，其中每一个小括号()为解向量，表示一种选择，里面有3个数，代表这种选择中3个商品是否装入背包。0表示装入，1表示不装入。如(0, 0, 1)表示的情况是商品1、2均不装入背包，商品3装入背包，此时背包装入商品的总重量为15，总价值为25，且未超过背包的重量限制值30。显然(0, 1, 1)是本例中最优的选择，即把商品2、3装入背包，商品1不装，此时背包装入商品的总重量为30，总价值为50，且满足重量限制的条件。

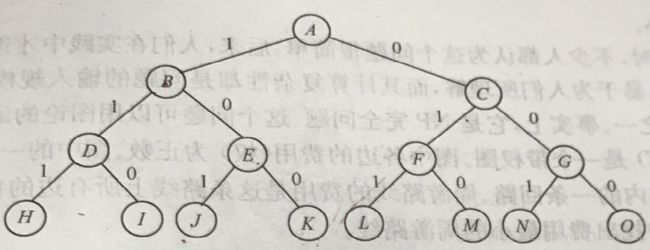
        基于搜索的算法解决时，都要先写出解空间和解向量，并以此生成解空间树，如图1所示。树分枝上方的1表示选择该商品放入背包，0表示不选该商品。除了根节点，树一共有3层，表示3个商品的选择与否。当遍历完所有叶节点，即得到了所有的结果。但是搜索的顺序如何确定呢？这就是回溯法和分枝限界的第一点区别。回溯法是以深度优先方式搜索整棵树，而分枝限界法是以广度优先或以最小耗费来搜索的。具体来说，分枝限界分为两种：队列式分枝限界和优先队列式分枝限界。这一点很重要，队列式分枝限界(数据结构为队列，先进先出)采用的是广度优先的搜索，优先队列式分枝限界(数据结构为优先级队列，也能是其他的数据结构)采用的是优先级高的优先搜索，高优先级的定义往往是最小耗费或最大效益。

        先简单介绍几个概念，下面会用到。扩展节点：一个正在产生儿子的节点；活节点：一个自身已生成，但是其儿子节点还没有全部生成的节点；死节点：一个所有儿子节点已经产生的节点。

    图1 0-1背包问题的解空间树

2.1.回溯法

        回溯法从根节点A开始搜索，此时A是唯一的活节点。A可以扩展到节点B或C。假设先到B(节点B、C哪个先扩展，不影响最终结果)，即把商品1装入背包，所以背包的剩余容量为14，此时背包的价值是45。活节点列表为{A, B}，节点B成为当前的扩展节点。B节点可以深度搜索到节点D或者E。若到达D，背包总重量将达到31，不满足条件，故剪去该分枝。当选择节点E，表示商品2不装入背包，所以一定满足条件。因此搜索到节点E，此时活节点列表为{A, B, E}，背包的剩余容量为14，此时背包的价值仍是45。节点E可以向下移至节点J或K。与D节点类似，J节点不是可行解。但是K节点可以选择，由于到了叶节点，所以得到了一个可行解(1, 0, 0)，暂时得到的背包最大价值bestv为45。因为K无法向下扩展，所以变为死节点，返回到E，仍是死节点，再返回到B，也是死节点。所以节点A再次成为扩展节点，到达节点C，此时的活节点列表为{A, C}，背包的剩余容量为30，背包的价值是0。节点C往下扩展，假设先扩展节点F，此时的活节点列表为{A, C, F}，背包的剩余容量为15，背包的价值是25。F再往下扩展至L，此时背包的剩余容量为0，背包的价值是50。由于已经到了叶节点，且50>bestv，所以更新bestv为50，记录此时的解向量(0, 1, 1)。这是更加活节点列表，返回到F，继续搜索，但是到了M，其背部的总价并未超过bestv，故舍去。同理，再搜索G及其子节点，最终当活节点列表为空时，算法结束，输出bestv和其对应的解向量(0, 1, 1)。

        当然，可以设计更好的剪枝函数，来简化搜索的过程，提高算法的效率，本文省去这一步骤。

2.2.队列式分枝限界法

        该方法是广度优先搜索。初始时，队列为空，节点A为当前扩展节点。节点A的2个儿子节点B、C均为可行节点，所以把B、C按从左到右的顺序加入列表中。由于A已经扩展出所有儿子节点，所以出队。此时的活节点列表(可以看做是一个队列，左边出队，右侧入队)为{B, C}，B和C哪个排在前面都行，不影响算法，因为这两种情况都属于广度优先搜索。按先进先出的原则，下一扩展节点为B，扩展后得到节点D和E。但是节点D不是可行解，故舍去。此时的活节点列表为{C, E}。接着C成为新的扩展节点，生成节点F、G。由于两个节点都是可行解，所以此时的活节点列表为{E, F, G}。再把E当做扩展节点，得到节点J、K。节点J不是可行解，舍去。节点K可行，且已到达叶节点，所以得到了暂时的最大背包重量bestv=45和其对应的解向量(1, 0, 0)，这时的活节点列表为{F, G}。把F当做扩展节点，L和M均是可行解，且到达叶节点。L这个分枝的背包重量为50>bestv，M分枝的背包重量是25，所以更新bestv=50，更新解向量为(0, 1, 1)，这时的活节点列表为{G}。把G扩展成节点N和O。但是这两个节点的背包最大重量均未超过bestv，所以舍去。此时活节点列表为空，算法结束，输出最优值bestv和解向量。

2.3优先队列式分枝限界法

        优先队列式分枝限界法首先要定义优先级。0-1背包问题主要有两种优先级定义的方法，一种是把已搜商品的最大价值定义为高优先级；另一种是定义已搜的与未搜的可能放入的最大商品价值的和较高的拥有高优先级。本例中采用第一种优先级的定义方式。优先队列式和队列式分枝限界法的区别就在于活节点队列中，节点的顺序不同，优先队列式节点的顺序是按优先级高低排序的，先搜优先级高的，所以不一定是广度优先搜索；而队列式是把一层搜完再搜下一层，属于广度优先搜索。

        优先队列式采用的数据结构可以是优先级队列(如c++中的priority_queue)。初始时，队列为空。扩展A，得到它的两个儿子节点B和C。这两个节点都是可行节点，加入到队列中，节点A出队。节点B获得的价值是45，而节点C若选择，获得的价值是0，所以节点B的优先级高于节点C，此时活节点列表为{B, C}，B排在C前面是因为计算优先级后B的大，此处二者顺序不能换。B成为下一扩展节点，得到节点D和E。D不是可行解，舍去。E是可行解，加入活节点队列，这时已搜背包的总价值仍为45，活节点列表为{E, C}，E节点的优先级高于C的。接着扩展E，得到叶节点J和K。J不可行，舍去。K可行，且到达叶节点，得到了暂时的最大背包重量bestv=45和其对应的解向量(1, 0, 0)。此时活节点列表为{C}。扩展了C后，得到节点F和G。F的已搜商品的最大价值为25，G的最大价值为0，所以F的优先级高于G，此时活节点列表为{F, G}。扩展F，得到两个儿子节点L和M。L的最大价值为50>bestv，所以更新bestv=50，更新解向量为(0, 1, 1)。在搜G的子节点，均未大于bestv。队列为空，算法结束。

3.例子二(旅行售货员问题)

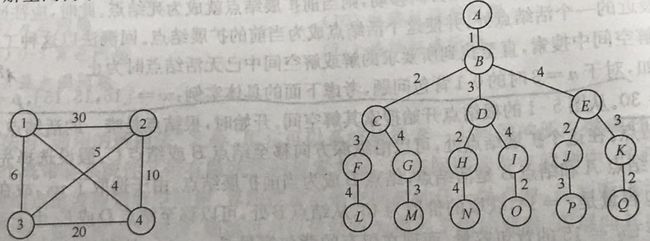
        旅行售货员问题是指某售货员要到若干个城市去推销商品，已知各个城市间的连接关系及路程(花费)。该售货员要从某一给定的城市出发，选择一条路径，能途径每一个城市，最后返回到出发的城市，且总的路程(花费)最小。如图2所示，1、2、3、4是四个城市，两个城市间的数字是这两个城市间的路程，如城市1与城市3之间的路程(花费)是6。序列1,2,4,3,1是一条可行路径，对应于解空间树中的A, B, C, G, M这条路径。

                                                                            图2 旅行售货员问题的解空间树

3.1.回溯法

        与0-1背包的过程类似，回溯法会先一路搜索到叶节点，即A->B->C->F->L，得到费用为59，暂时的bestv=59。之后返回到C，再搜索A->B->C->G->M，费用为66>bestv，所以舍去。按部就班地搜索后面的分枝，最终可以得到最优解：A->B->D->H->N，即从城市1->3->2->4->1。剪枝函数可以设计为剪去那些无法返回到城市1的分枝和费用超过bestv的分枝，以提高搜索速度。

3.2.队列式分枝限界法

        初始时，把B当做扩展节点，活节点队列为空。B扩展后，把节点C、D、E加入活节点列表，此时的活节点列表为{C, D, E}。C成为下一个扩展节点，扩展出F和G。之后依次扩展节点D和E，节点D、E扩展完后，活节点列表变为{F, G, H, I, J, K}。F成为下一扩展节点。此时到达叶节点，得到暂时的bestv=59。之后G扩展为M，计算费用值为66，大于bestv，故舍去。后面的节点以此类推，直至活节点列表为空，算法结束，输出bestv=25和对应的路径A->B->D->H->N。

3.3优先队列式分枝限界法

        优先级定义为售货员当前已经过城市的总花费。初始时，扩展节点B，得到3个儿子节点C、D、E。由于这3段路程的花费为30>6>4，所以活节点列表的顺序为{E, D, C}，左边的优先级高，先扩展。E扩展后，得到J和K，对应的费用为14和24，所以活节点队列变为{D, J, K, C}。接下去扩展节点D，得到节点H和I。从B到达H的费用为11，从B到达I的费用为26，所以活节点队列变为{H, J, K, I, C}。扩展H后，到达叶节点N，得到一条回路1->3->2->4->1，bestv=25，此时活节点队列变为{J, K, I, C}。扩展K，得到另一条路径，但其费用未低于25，舍去。之后扩展K，可行解费用超过bestv，舍去。扩展I，本身的费用已超过bestv，I及之后的节点均无需再计算，舍去。最后列表为空，输出结果。

4.总结

        通过以上两个实例，回溯法和分枝限界法的算法流程应该能大体掌握。当然，要深入了解这两个算法，仍需进一步学习如何构建解空间，是用排列树还是子集树、剪枝函数如何定义、如何编程实现等等不一而足。最后梳理一下回溯法和分枝限界法的主要区别。

• 回溯法

        求解目标：找出解空间中满足条件的所有解；

        搜索方式：以深度优先的方式搜索；

        扩展方式：扩展节点基本不会一次产生所有儿子节点。

• 分枝限界法

        求解目标：找出解空间中满足条件的一个解，或者最优解；

        搜索方式：以广度优先的方式或以最小耗费的方式搜索；

        扩展方式：活节点一旦产生扩展节点，则一次性产生其所有儿子节点。