十种排序算法

1.常见算法分类

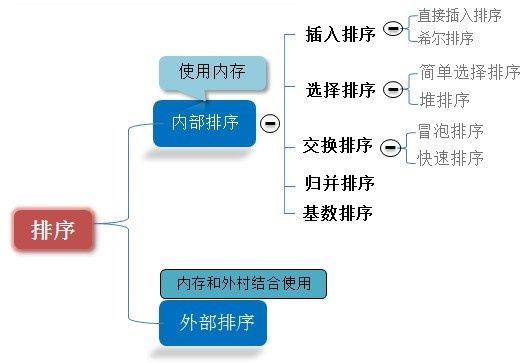
十种常见排序算法一般分为以下几种： 
（1）非线性时间比较类排序：交换类排序（快速排序和冒泡排序）、插入类排序（简单插入排序和希尔排序）、选择类排序（简单选择排序和堆排序）、归并排序（二路归并排序和多路归并排序）；

（2）线性时间非比较类排序：计数排序、基数排序和桶排序。

总结： 
（1）在比较类排序中，归并排序号称最快，其次是快速排序和堆排序，两者不相伯仲，但是有一点需要注意，数据初始排序状态对堆排序不会产生太大的影响，而快速排序却恰恰相反。

（2）线性时间非比较类排序一般要优于非线性时间比较类排序，但前者对待排序元素的要求较为严格，比如计数排序要求待排序数的最大值不能太大，桶排序要求元素按照hash分桶后桶内元素的数量要均匀。线性时间非比较类排序的典型特点是以空间换时间。

注：本博文的示例代码均已递增排序为目的。

---

2.算法描述与实现

2.1交换类排序

交换排序的基本方法是：两两比较待排序记录的排序码，交换不满足顺序要求的偶对，直到全部满足位置。常见的冒泡排序和快速排序就属于交换类排序。

2.1.1冒泡排序

算法思想： 
从数组中第一个数开始，依次遍历数组中的每一个数，通过相邻比较交换，每一轮循环下来找出剩余未排序数的中的最大数并”冒泡”至数列的顶端。

算法步骤： 
（1）从数组中第一个数开始，依次与下一个数比较并次交换比自己小的数，直到最后一个数。如果发生交换，则继续下面的步骤，如果未发生交换，则数组有序，排序结束，此时时间复杂度为O(n)； 
（2）每一轮”冒泡”结束后，最大的数将出现在乱序数列的最后一位。重复步骤（1）。

稳定性：稳定排序。

时间复杂度： O(n)至O(n2)，平均时间复杂度为O(n2)。

最好的情况：如果待排序数据序列为正序，则一趟冒泡就可完成排序，排序码的比较次数为n-1次，且没有移动，时间复杂度为O(n)。

最坏的情况：如果待排序数据序列为逆序，则冒泡排序需要n-1次趟起泡，每趟进行n-i次排序码的比较和移动，即比较和移动次数均达到最大值： 
比较次数:Cmax=∑i=1n−1(n−i)=n(n−1)/2=O(n2) 
移动次数等于比较次数，因此最坏时间复杂度为O(n2)。

示例代码：

void bubbleSort(int array[],int len){
    //循环的次数为数组长度减一，剩下的一个数不需要排序
    for(int i=0;i1;++i){
        bool noswap=true;
        //循环次数为待排序数第一位数冒泡至最高位的比较次数
        for(int j=0;j1;++j){
            if(array[j]>array[j+1]){
                array[j]=array[j]+array[j+1];
                array[j+1]=array[j]-array[j+1];
                array[j]=array[j]-array[j+1];
                //交换或者使用如下方式
                //a=a^b;
                //b=b^a;
                //a=a^b;
                noswap=false;
            }
        }
        if(noswap) break;
    }
}

2.1.2快速排序

冒泡排序是在相邻的两个记录进行比较和交换，每次交换只能上移或下移一个位置，导致总的比较与移动次数较多。快速排序又称分区交换排序，是对冒泡排序的改进，快速排序采用的思想是分治思想。。

算法原理： 
(1)从待排序的n个记录中任意选取一个记录（通常选取第一个记录）为分区标准;

(2)把所有小于该排序列的记录移动到左边，把所有大于该排序码的记录移动到右边，中间放所选记录，称之为第一趟排序；

(3)然后对前后两个子序列分别重复上述过程，直到所有记录都排好序。

稳定性：不稳定排序。

时间复杂度： O（nlog2n）至O(n2)，平均时间复杂度为O（nlgn）。

最好的情况：是每趟排序结束后，每次划分使两个子文件的长度大致相等，时间复杂度为O（nlog2n）。

最坏的情况：是待排序记录已经排好序，第一趟经过n-1次比较后第一个记录保持位置不变，并得到一个n-1个元素的子记录；第二趟经过n-2次比较，将第二个记录定位在原来的位置上，并得到一个包括n-2个记录的子文件，依次类推，这样总的比较次数是： 

Cmax=∑i=1n−1(n−i)=n(n−1)/2=O(n2)

 

示例代码：

//a：待排序数组，low：最低位的下标，high：最高位的下标
void quickSort(int a[],int low, int high)
{
    if(low>=high)
    {
        return;
    }
    int left=low;
    int right=high;
    int key=a[left];    /*用数组的第一个记录作为分区元素*/
    while(left!=right){
        while(left=key)    /*从右向左扫描，找第一个码值小于key的记录，并交换到key*/
            --right;
        a[left]=a[right];
        while(left/*从左向右扫描，找第一个码值大于key的记录，并交换到右边*/
    }
    a[left]=key;    /*分区元素放到正确位置*/
    quickSort(a,low,left-1);
    quickSort(a,left+1,high);
}

---

2.2插入类排序

插入排序的基本方法是：每步将一个待排序的记录，按其排序码大小，插到前面已经排序的文件中的适当位置，直到全部插入完为止。

2.2.1直接插入排序

原理：从待排序的n个记录中的第二个记录开始，依次与前面的记录比较并寻找插入的位置，每次外循环结束后，将当前的数插入到合适的位置。

稳定性：稳定排序。

时间复杂度： O(n)至O（n2），平均时间复杂度是O（n2）。

最好情况：当待排序记录已经有序，这时需要比较的次数是Cmin=n−1=O(n)。

最坏情况：如果待排序记录为逆序，则最多的比较次数为Cmax=∑i=1n−1(i)=n(n−1)2=O(n2)。

示例代码：

//A：输入数组，len:数组长度
void insertSort(int A[],int len)
{
    int temp;
    for(int i=1;iint j=i-1;
      temp=A[i]; 
      //查找到要插入的位置
      while(j>=0&&A[j]>temp)
      {
          A[j+1]=A[j];
          j--;
      }
      if(j!=i-1)
        A[j+1]=temp;
    }
}

2.2.2 Shell排序

Shell 排序又称缩小增量排序, 由D. L. Shell在1959年提出，是对直接插入排序的改进。

原理： Shell排序法是对相邻指定距离(称为增量)的元素进行比较，并不断把增量缩小至1，完成排序。

Shell排序开始时增量较大，分组较多，每组的记录数目较少，故在各组内采用直接插入排序较快，后来增量di逐渐缩小，分组数减少，各组的记录数增多，但由于已经按di−1分组排序，文件叫接近于有序状态，所以新的一趟排序过程较快。因此Shell排序在效率上比直接插入排序有较大的改进。

在直接插入排序的基础上，将直接插入排序中的1全部改变成增量d即可，因为Shell排序最后一轮的增量d就为1。

稳定性：不稳定排序。

时间复杂度：O(n1.3)到O(n2)。Shell排序算法的时间复杂度分析比较复杂，实际所需的时间取决于各次排序时增量的个数和增量的取值。研究证明，若增量的取值比较合理，Shell排序算法的时间复杂度约为O(n1.3)。

对于增量的选择，Shell 最初建议增量选择为n/2，并且对增量取半直到 1；D. Knuth教授建议di+1=⌊di−13⌋序列。

//A：输入数组，len:数组长度，d:初始增量(分组数)
void shellSort(int A[],int len, int d)
{
    for(int inc=d;inc>0;inc/=2){        //循环的次数为增量缩小至1的次数
        for(int i=inc;i//循环的次数为第一个分组的第二个元素到数组的结束
            int j=i-inc;
            int temp=A[i];
            while(j>=0&&A[j]>temp)
            {
                A[j+inc]=A[j];
                j=j-inc;
            }
            if((j+inc)!=i)//防止自我插入
                A[j+inc]=temp;//插入记录
        }
    }
}

注意：从代码中可以看出，增量每次变化取前一次增量的一般，当增量d等于1时，shell排序就退化成了直接插入排序了。

---

2.3选择类排序

选择类排序的基本方法是：每步从待排序记录中选出排序码最小的记录，顺序放在已排序的记录序列的后面，知道全部排完。

2.3.1简单选择排序（又称直接选择排序）

原理：从所有记录中选出最小的一个数据元素与第一个位置的记录交换；然后在剩下的记录当中再找最小的与第二个位置的记录交换，循环到只剩下最后一个数据元素为止。

稳定性：不稳定排序。

时间复杂度： 最坏、最好和平均复杂度均为O(n2)，因此，简单选择排序也是常见排序算法中性能最差的排序算法。简单选择排序的比较次数与文件的初始状态没有关系，在第i趟排序中选出最小排序码的记录，需要做n-i次比较，因此总的比较次数是：∑i=1n−1(n−i)=n(n−1)/2=O(n2)。

示例代码：

void selectSort(int A[],int len)
{
    int i,j,k;
    for(i=0;i
       k=i;
       for(j=i+1;j
           if(A[j]<A[k])
               k=j;
       }
       if(i!=k){
           A[i]=A[i]+A[k];
           A[k]=A[i]-A[k];
           A[i]=A[i]-A[k];
       }
    }
}

2.3.2堆排序

直接选择排序中，第一次选择经过了n-1次比较，只是从排序码序列中选出了一个最小的排序码，而没有保存其他中间比较结果。所以后一趟排序时又要重复许多比较操作，降低了效率。J. Willioms和Floyd在1964年提出了堆排序方法，避免这一缺点。

堆的性质： 
（1）性质：完全二叉树或者是近似完全二叉树； 
（2）分类：大顶堆：父节点不小于子节点键值，小顶堆：父节点不大于子节点键值；图展示一个最小堆： 

（3）左右孩子：没有大小的顺序。

（4）堆的存储 
一般都用数组来存储堆，i结点的父结点下标就为(i–1)/2。它的左右子结点下标分别为 2∗i+1 和 2∗i+2。如第0个结点左右子结点下标分别为1和2。 

（5）堆的操作 
建立： 
以最小堆为例，如果以数组存储元素时，一个数组具有对应的树表示形式，但树并不满足堆的条件，需要重新排列元素，可以建立“堆化”的树。

 

插入： 
将一个新元素插入到表尾，即数组末尾时，如果新构成的二叉树不满足堆的性质，需要重新排列元素，下图演示了插入15时，堆的调整。

删除： 
堆排序中，删除一个元素总是发生在堆顶，因为堆顶的元素是最小的（小顶堆中）。表中最后一个元素用来填补空缺位置，结果树被更新以满足堆条件。

 

稳定性：不稳定排序。

插入代码实现： 
每次插入都是将新数据放在数组最后。可以发现从这个新数据的父结点到根结点必然为一个有序的数列，现在的任务是将这个新数据插入到这个有序数据中，这就类似于直接插入排序中将一个数据并入到有序区间中，这是节点“上浮”调整。不难写出插入一个新数据时堆的调整代码：

//新加入i结点,其父结点为(i-1)/2
//参数：a：数组，i：新插入元素在数组中的下标  
void minHeapFixUp(int a[], int i)  
{  
    int j, temp;  
    temp = a[i];  
    j = (i-1)/2;      //父结点  
    while (j >= 0 && i != 0)  
    {  
        if (a[j] <= temp)//如果父节点不大于新插入的元素，停止寻找  
            break;  
        a[i]=a[j];     //把较大的子结点往下移动,替换它的子结点  
        i = j;  
        j = (i-1)/2;  
    }  
    a[i] = temp;  
}  

因此，插入数据到最小堆时：

//在最小堆中加入新的数据data  
//a：数组，index：插入的下标，
void minHeapAddNumber(int a[], int index, int data)  
{  
    a[index] = data;  
    minHeapFixUp(a, index);  
} 

删除代码实现： 
按定义，堆中每次都只能删除第0个数据。为了便于重建堆，实际的操作是将数组最后一个数据与根结点，然后再从根结点开始进行一次从上向下的调整。

调整时先在左右儿子结点中找最小的，如果父结点不大于这个最小的子结点说明不需要调整了，反之将最小的子节点换到父结点的位置。此时父节点实际上并不需要换到最小子节点的位置，因为这不是父节点的最终位置。但逻辑上父节点替换了最小的子节点，然后再考虑父节点对后面的结点的影响。相当于从根结点将一个数据的“下沉”过程。下面给出代码：

//a为数组，从index节点开始调整,len为节点总数 从0开始计算index节点的子节点为 2*index+1, 2*index+2,len/2-1为最后一个非叶子节点  
void minHeapFixDown(int a[],int len,int index){
    if(index>(len/2-1))//index为叶子节点不用调整
        return;
    int tmp=a[index];
    int lastIndex=index;
    while(index<=(len/2-1)){ //当下沉到叶子节点时，就不用调整了
        if(a[2*index+1]//如果左子节点大于该节点
            lastIndex = 2*index+1;
        //如果存在右子节点且大于左子节点和该节点
        if(2*index+22*index+2]2*index+1]&& a[2*index+2]2*index+2;
        if(lastIndex!=index){  //如果左右子节点有一个小于该节点则设置该节点的下沉位置
            a[index]=a[lastIndex];
            index=lastIndex;
        }else break;  //否则该节点不用下沉调整
    }
    a[lastIndex]=tmp;//将该节点放到最后的位置
}

根据思想，可以有不同版本的代码实现，以上是和孙凛同学一起讨论出的一个版本，在这里感谢他的参与，读者可另行给出。个人体会，这里建议大家根据对堆调整的过程的理解，写出自己的代码，切勿看示例代码去理解算法，而是理解算法思想写出代码，否则很快就会忘记。

建堆： 
有了堆的插入和删除后，再考虑下如何对一个数据进行堆化操作。要一个一个的从数组中取出数据来建立堆吧，不用！先看一个数组，如下图：

 

很明显，对叶子结点来说，可以认为它已经是一个合法的堆了即20，60， 65， 4， 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30，A[2] = 17，A[1] = 12，A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤：

 

写出堆化数组的代码：

//建立最小堆
//a:数组，n：数组长度
void makeMinHeap(int a[], int n)  
{  
    for (int i = n/2-1; i >= 0; i--)  
        minHeapFixDown(a, i, n);  
}  

（6）堆排序的实现 
由于堆也是用数组来存储的，故对数组进行堆化后，第一次将A[0]与A[n - 1]交换，再对A[0…n-2]重新恢复堆。第二次将A[0]与A[n – 2]交换，再对A[0…n - 3]重新恢复堆，重复这样的操作直到A[0]与A[1]交换。由于每次都是将最小的数据并入到后面的有序区间，故操作完成后整个数组就有序了。有点类似于直接选择排序。

因此，完成堆排序并没有用到前面说明的插入操作，只用到了建堆和节点向下调整的操作，堆排序的操作如下：

//array:待排序数组，len：数组长度
void heapSort(int array[],int len){
    //建堆
    makeMinHeap(array, len); 
    //根节点和最后一个叶子节点交换，并进行堆调整，交换的次数为len-1次
    for(int i=0;i1;++i){
        //根节点和最后一个叶子节点交换
        array[0] += array[len-i-1];  
        array[len-i-1] = array[0]-array[len-i-1];  
        array[0] = array[0]-array[len-i-1];

        //堆调整
        minHeapFixDown(array, 0, len-i-1);  
    }
}  

（7）堆排序的性能分析 

由于每次重新恢复堆的时间复杂度为O(logN)，共N - 1次堆调整操作，再加上前面建立堆时N / 2次向下调整，每次调整时间复杂度也为O(logN)。两次次操作时间相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。

最坏情况：如果待排序数组是有序的，仍然需要O(N * logN)复杂度的比较操作，只是少了移动的操作；

最好情况：如果待排序数组是逆序的，不仅需要O(N * logN)复杂度的比较操作，而且需要O(N * logN)复杂度的交换操作。总的时间复杂度还是O(N * logN)。

因此，堆排序和快速排序在效率上是差不多的，但是堆排序一般优于快速排序的重要一点是，数据的初始分布情况对堆排序的效率没有大的影响。

---

2.4归并排序

算法思想： 
归并排序属于比较类非线性时间排序，号称比较类排序中性能最佳者，在数据中应用中较广。

归并排序是分治法（Divide and Conquer）的一个典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

稳定性：稳定排序算法；

时间复杂度: 最坏，最好和平均时间复杂度都是Θ(nlgn)。

具体的实现见本人的另一篇blog：二路归并排序简介及其并行化。

---

2.5线性时间非比较类排序

2.5.1计数排序

计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出，它的优势在于在对于较小范围内的整数排序。它的复杂度为Ο(n+k)（其中k是待排序数的范围），快于任何比较排序算法，缺点就是非常消耗空间。很明显，如果而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序，比如堆排序和归并排序和快速排序。

算法原理： 
基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，在代码中作适当的修改即可。

算法步骤： 
（1）找出待排序的数组中最大的元素； 
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项； 
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）； 
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

时间复杂度：Ο(n+k)。

空间复杂度：Ο(k)。

要求：待排序数中最大数值不能太大。

稳定性：稳定。

代码示例：

#define MAXNUM 20    //待排序数的最大个数
#define MAX    100   //待排序数的最大值
int sorted_arr[MAXNUM]={0};

//计算排序
//arr:待排序数组，sorted_arr：排好序的数组，n：待排序数组长度
void countSort(int *arr, int *sorted_arr, int n)  
{   
    int i;   
    int *count_arr = (int *)malloc(sizeof(int) * (MAX+1));  

    //初始化计数数组   
    memset(count_arr,0,sizeof(int) * (MAX+1));

    //统计i的次数   
    for(i = 0;i//对所有的计数累加，作用是统计arr数组值和小于小于arr数组值出现的个数
    for(i = 1; i<=MAX; i++)  
        count_arr[i] += count_arr[i-1];   
    //逆向遍历源数组（保证稳定性），根据计数数组中对应的值填充到新的数组中   
    for(i = n-1; i>=0; i--)  
    {  
        //count_arr[arr[i]]表示arr数组中包括arr[i]和小于arr[i]的总数
        sorted_arr[count_arr[arr[i]]-1] = arr[i];  

        //如果arr数组中有相同的数，arr[i]的下标减一
        count_arr[arr[i]]--;    
    }
    free(count_arr);
}

注意：计数排序是典型的以空间换时间的排序算法，对待排序的数据有严格的要求，比如待排序的数值中包含负数，最大值都有限制，请谨慎使用。

2.5.2基数排序

基数排序属于“分配式排序”（distribution sort），是非比较类线性时间排序的一种，又称“桶子法”（bucket sort）。顾名思义，它是透过键值的部分信息，将要排序的元素分配至某些“桶”中，藉以达到排序的作用。

具体描述即代码示例见本人另一篇blog:基数排序简介及其并行化。

2.5.3桶排序

桶排序也是分配排序的一种，但其是基于比较排序的，这也是与基数排序最大的区别所在。

思想：桶排序算法想法类似于散列表。首先要假设待排序的元素输入符合某种均匀分布，例如数据均匀分布在[ 0,1）区间上，则可将此区间划分为10个小区间，称为桶，对散布到同一个桶中的元素再排序。

要求：待排序数长度一致。

排序过程： 
（1）设置一个定量的数组当作空桶子； 
（2）寻访序列，并且把记录一个一个放到对应的桶子去； 
（3）对每个不是空的桶子进行排序。 
（4）从不是空的桶子里把项目再放回原来的序列中。

例如待排序列K= {49、 38 、 35、 97 、 76、 73 、 27、 49 }。这些数据全部在1—100之间。因此我们定制10个桶，然后确定映射函数f(k)=k/10。则第一个关键字49将定位到第4个桶中(49/10=4)。依次将所有关键字全部堆入桶中，并在每个非空的桶中进行快速排序。

时间复杂度： 
对N个关键字进行桶排序的时间复杂度分为两个部分： 
(1) 循环计算每个关键字的桶映射函数，这个时间复杂度是O(N)。

(2) 利用先进的比较排序算法对每个桶内的所有数据进行排序，对于N个待排数据，M个桶，平均每个桶[N/M]个数据，则桶内排序的时间复杂度为 ∑i=1MO(Ni∗logNi)=O(N∗logNM) 。其中Ni 为第i个桶的数据量。

因此，平均时间复杂度为线性的O(N+C)，C为桶内排序所花费的时间。当每个桶只有一个数，则最好的时间复杂度为：O(N)。

示例代码：

typedef struct node
 { 
     int keyNum;//桶中数的数量
     int key;   //存储的元素
     struct node * next;  
 }KeyNode;    

 //keys待排序数组，size数组长度，bucket_size桶的数量
 void inc_sort(int keys[],int size,int bucket_size)
 { 
     KeyNode* k=(KeyNode *)malloc(sizeof(KeyNode)); //用于控制打印
     int i,j,b;
     KeyNode **bucket_table=(KeyNode **)malloc(bucket_size*sizeof(KeyNode *)); 
     for(i=0;i*)malloc(sizeof(KeyNode)); 
         bucket_table[i]->keyNum=0;//记录当前桶中是否有数据
         bucket_table[i]->key=0;   //记录当前桶中的数据  
         bucket_table[i]->next=NULL; 
     }    

     for(j=0;jint index;
         KeyNode *p;
         KeyNode *node=(KeyNode *)malloc(sizeof(KeyNode));   
         node->key=keys[j];  
         node->next=NULL;  

         index=keys[j]/10;        //映射函数计算桶号  
         p=bucket_table[index];   //初始化P成为桶中数据链表的头指针  
         if(p->keyNum==0)//该桶中还没有数据 
         {    
             bucket_table[index]->next=node;    
             (bucket_table[index]->keyNum)++;  //桶的头结点记录桶内元素各数，此处加一
         }
         else//该桶中已有数据 
         {   
             //链表结构的插入排序 
             while(p->next!=NULL&&p->next->key<=node->key)   
                 p=p->next;    
             node->next=p->next;     
             p->next=node;      
             (bucket_table[index]->keyNum)++;   
         }
     }
     //打印结果
     for(b=0;bfor(k=bucket_table[b];k->next!=NULL;k=k->next)  
         {
             printf("%d ",k->next->key);
         }
 }