【Atcoder】AGC008 B-F简要题解
B.Contiguous Repainting
不管怎么操作,最后一定有连续的 K K K个颜色相同,其它的格子可以随便染。
枚举这 K K K个颜色相同的区间即可。
C.Tetromino Tiling
研究一下四米诺的组合:
- T,S,Z根本放不上去
- O可以全部直接放上去
- 剩下的组合只有: 2L,2J,2*I,L+J+I
分类讨论即可。
D.K-th K
贪心往前放就是了
E.Next or Nextnext
再次读错题浪费时间:
For each 1 ≤ i ≤ N 1\leq i\leq N 1≤i≤N,at least one of the following holds: p i = a i p_i=a_i pi=aiand p p i = a i p_{p_i}=a_i ppi=ai
读成了至少有两个 i i i分别满足 p i = a i p_i=a_i pi=ai, p p i = a i p_{p_i}=a_i ppi=ai…
我服我自己。。。
emmm,一道神奇的基环树森林结论题:
p → a p\to a p→a
p p p是一个 1 − N 1-N 1−N的排列,所以构图 i → p i i\to p_i i→pi,得到若干个环。
在 p p p变化成 a a a的过程中,每个点要么保持 i → p i i\to p_i i→pi,要么转化成 i → p p i i\to p_{p_i} i→ppi,分类讨论:
- 保持原状,即 p i = a i ( 1 ≤ i ≤ N ) p_i=a_i(1\leq i\leq N) pi=ai(1≤i≤N),图的形态不变
- 所有 i i i指向 p p i p_{p_i} ppi,即 p p i = a I ( 1 ≤ i ≤ N ) p_{p_i}=a_I(1\leq i\leq N) ppi=aI(1≤i≤N)
对于奇环,变成同构的另一个环。
对于偶环,拆分成偶数点和奇数点分别构成的两个大小相同的环。 - 若环中部分点指向 p i p_i pi,部分点指向 p p i p_{p_i} ppi,则变成了一棵由一个环和若干指向环的链构成的基环内向树。
a → p a\to p a→p
考虑由 a a a反推 p p p:
- 单独考虑每个大小的环,组合一下
- 对于一颗基环内向树,找到所有相邻的指向环的链,假设当前链边数为 a a a,链顶与上一个链顶在环上的距离边数为 b b b:
若 b < a b<a b<a,有0种方案;若 a = b a=b a=b有1种方案;若 a < b a<b a<b,有2种方案。
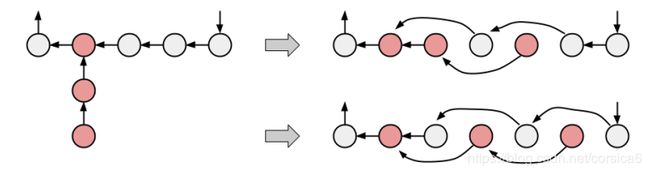
乘法原理合并即可。
#includeF.Black Radius
先假设树上所有点都是关键点:
设 f ( x , d ) f(x,d) f(x,d)表示距离 x x x小于等于 d d d的点集合。
为避免算重,对于所有集合相同的 f ( x , d ) f(x,d) f(x,d)只取 d d d最小的一个计入答案。
不考虑 f ( x , d ) f(x,d) f(x,d)为全集的情况(最后再 a n s + 1 ans+1 ans+1),所需要求出的就是:
d i d_i di:最大的 d d d满足 f ( i , 0 − d ) f(i,0-d) f(i,0−d)均可取且 f ( x , d i ) f(x,d_i) f(x,di)不为全集。
上界 d i d_i di的具体求法:
将点 i i i作为根,设离 i i i最远的点的距离为 m x i mx_i mxi,显然 d i < m x i d_i<mx_i di<mxi,且 ∀ j ∈ s o n i \forall j\in son_i ∀j∈soni, ∃ f ( i , d ) ≠ f ( j , d − 1 ) \exists f(i,d)\neq f(j,d-1) ∃f(i,d)̸=f(j,d−1)。
设删掉 j j j子树后离 i i i最远的点的距离为 p m x i pmx_i pmxi,则 d i − 2 < p m x i d_i-2<pmx_i di−2<pmxi。
故 d i = min ( max ( p m x i ) + 1 , m x i − 1 ) d_i=\min(\max(pmx_i)+1,mx_i-1) di=min(max(pmxi)+1,mxi−1)。
考虑有些点不是关键点的情况:
那么对于每个非关键点存在一个下界 q i q_i qi:最小的 q q q满足 f ( q , d i ) f(q,d_i) f(q,di)均可取且为某个关键点 f ( j , d ) f(j,d) f(j,d)的点集。
下界 q i q_i qi的具体求法:
将点 i i i看做根,考虑 j ∈ s o n i j\in son_i j∈soni的所有的内部有关键点的子树 j ′ j' j′, q i = max ( m a x d e p j ′ ) q_i=\max(maxdep_{j'}) qi=max(maxdepj′),即 f ( i , q i ) f(i,q_i) f(i,qi)必须要把这些子树全部覆盖。
2遍 d f s dfs dfs求得 d i , q i d_i,q_i di,qi。