线性表(数组、单链表、静态链表、循环链表、双向链表)
线性表的定义
线性表(List):零个或多个数据元素的有限序列。
有几个地方需要强调:
- 首先它是一个序列,也就是说元素之间是有顺序的,若元素存在多个,则第一个元素无前驱,最后一个元素无后继,其他每个元素都有且只有一个前驱和后继。
- 然后线性表强调的是有限的。
- 最后线性表中的数据元素必须是相同类型。
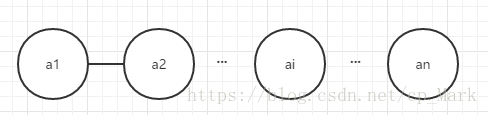
如果用数据语言来定义,可如下(配合下图理解):
数学语言定义: 若将线性表记为(a1,…,ai,…,an),则表中ai-₁领先于ai,ai领先于ai+₁,称ai-₁是ai的直接前驱元素,ai+₁是ai的直接后继元素。当i=1,2,…,n-1时,ai有且仅有一个直接后继,当i=2,…,n时,ai有且仅有一个直接前驱。
线性表元素的个数n(n≧0)定义为线性表的长度,当n=0时,称为空表。
一个线性表中的数据元素ai,i称为数据元素ai在线性表中的位序。
线性表的抽象数据类型
线性表常见的操作如下:
- 创建和初始化
- 重置
- 根据位序获取数据元素
- 查找某数据元素是否存在
- 获得线性表长度
- 插入数据
- 删除数据
根据以上的常见操作,线性表的抽象数据类型定义如下:
ADT 线性表(List)
Data
线性表的数据对象集合为{a1,a2,......,an},每个元素的类型均为DataType。其中除第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an外,每一个元素有且只有一个直接后继元素。数据元素之间的关系是一对一的关系。
Operation
InitList(*L): 初始化操作,建立一个空的线性表L。
ListEmpty(L): 若线性表为空,返回true,否则返回false。
ClearList(*L): 将线性表清空。
GetElem(L,i,*e): 将线性表L中的第i个位置的元素值返回给e。
LocateElem(L,e): 在线性表L中查找与给定值e相等的元素,如果查找成功,返回该元素在表中的序号表示成功;否则,返回0表示失败。
ListInsert(*L,i,e): 在线性表L中的第i个位置插入新元素e。
ListDelete(*L,i,*e): 删除线性表L中第i个位置元素,并用e返回其值
ListLength(L): 返回线性表L的元素个数
endADT
对于不同的应用,线性表的基本操作是不同的,上述操作时最基本的,对于实际问题中涉及的关于线性表的更复杂操作,我们可以用这些基本操作的组合来实现。
我们假设La表示集合A,Lb表示集合B,求两个集合的并集:
//将所有的在线性表Lb中但不在La中的数据元素插入到La中
void unionL(List *La,List *Lb){
int La_len,Lb_len,i;
//声明与La和Lb相同的数据元素e
ElemType e;
//求线性表的长度
La_len = ListLength(La);
Lb_len = ListLength(Lb);
for(i = 1; i <= Lb_len; i++){
//取Lb中第i个数据元素赋给e
GetElem(Lb,i,&e);
if(!LocateElem(*La,e)){
//插入
ListInsert(La,++La_len,e);
}
}
}
我们对于union操作,用到了前面线性表基本操作LocateElem,ListInsert,ListLength等,可见,对于复杂的个性化的操作,其实就是把基本操作组合起来实现的。
线性表的顺序存储结构
定义:线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。
在C语言中我们可以使用一维数组来实现顺序存储结构,即把第一个数据元素存到数组下标为0的位置中,接着把线性表相邻的元素存储在数组中相邻的位置。下面来看下线性表的顺序存储的结构代码:
//存储空间初始分配量
#define MAXSIZE 20
//ElemType类型根据实际情况而定,这里假设为int
typedef int ElemType;
typedef struct{
//数组存储数据元素,最大值为MAXSIZE
ElemType data[MAXSIZE];
//线性表当前长度
int length;
}SqList;
根据上面的定义,我们发现描述顺序存储结构需要三个属性:
- 存储空间的起始位置:数组data,它的存储位置就是存储空间的存储位置。
- 线性表的最大存储容量:数组长度MaxSize。
- 线性表的当前长度:length。
我们已知存储空间的起始位置,即数组data的存储位置,等同于数组中下标为0的元素的存储位置,所以已知下标为0的数据元素的存储位置 LOC(a0),假设每个数据元素所占的空间为c,那么第i个数据元素的存储位置LOC(ai)为:
- *LOC(ai) = LOC(a0) +(i -1)c
通过以上公式,我们可以随时算出线性表中任意位置的地址。此时我们对线性表中任意位置数据的读取和更新对于计算机来说时间都是相等的,也就是一个常数,其时间复杂度为常数阶O(1),我们把具有这一特点的存储结构称为随机存取结构。
注意数组长度和线性表长度的区别:
- 数组长度是存放线性表的存储空间的长度(即存储容量),分配之后一般是不变的。不过在高级语言中,可以用编程手段实现动态分配数组,不过这会带来性能上的损耗。
- 线性表的长度是线性表中数据元素的个数,随着线性表插入和删除操作的进行,这个量是变化的。
顺序存储结构的获取、插入和删除
-
数据元素的获取
对于线性表的顺序存储结构来说,我们要实现GetElem操作,即将线性表L中的第i个位置元素值返回即可。代码实现如下:
//顺序存储线性表获取特定下标i的数据元素值。时间复杂度为O(1)
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
//初始条件:顺序线性表L已存在,1<=i<=ListLength(L)
//操作结果:用e返回L中第i个数据元素的值
Status GetElem(SqList L,int i,ElemType *e){
if(L.length == 0 || i < 1 || i > L.length){
return Error;
}
*e = L.data[i - 1];
return OK;
}
-
插入操作
当我们要在线性表L中的第i个位置插入新元素e,即实现ListInsert(*L,i,e),该如何操作呢?当然是从数组的最后向前遍历到位置i,将这些元素全部后移一个位置,然后在i位置插入新的数据元素。代码实现如下:
//时间复杂度为O(n) //初始条件:顺序线性表L已存在,1<=i<=ListLength(L) //操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1 Status ListInsert(SqList *L,int i,ElemType e){ int k; //顺序线性表已满 if(L->length == MAXSIZE){ return ERROR; } //i不在范围内 if(i > L->length+1 || i < 1){ return ERROR; } //若插入数据位置不在表尾 if(i <= L->length){ //将要插入位置后面的数据元素后移一位 for(k = L->length - 1; k >= i - 1;k--){ L->data[k+1]=L->data[k]; } } //将新元素插入 L->data[i-1] = e; L->length++; return OK; } -
删除操作
当我们要删除线性表中第i个位置的数据元素,即实现ListDelete(*L,i,*e),该如何操作呢?当然是从删除位置开始遍历到最后一个元素位置,分别将它们都向前移动一个位置。代码实现如下:
//时间复杂度为O(n) //初始条件:顺序线性表L已存在,1<=i<=ListLength(L) //操作结果:删除L中第i个位置的数据元素,并用e返回其值,L的长度减1 Status ListDelete(SqList *L,int i,ElemType e){ int k; //空表 if(L->length == 0){ return ERROR; } //i不在范围内 if(i > L->length || i < 1){ return ERROR; } *e = L->data[i-1]; //若删除位置不在表尾 if(i < L->length){ //将删除位置的后继元素前移 for(k = i; k < L->length; k++){ L->data[k-1]=L->data[k]; } } L->length--; return OK; }
线性表顺序存储结构的优缺点
优点:
- 无须为表示表中元素之间的逻辑关系而增加额外的存储空间。
- 可以快速地存取表中任一位置的元素(存取时间复杂度为O(1))。
缺点:
- 插入和删除操作需要移动大量元素(以最坏情况来分析,插入和删除时间复杂度为O(n))。
- 当线性表长度变化较大时,难以确定存储空间的容量。
- 造成存储空间的“碎片”。即浪费,无法全部利用。
线性表的链式存储结构
线性表的顺序存储结构最大的缺点就是插入和删除时需要移动大量的元素,这显然就需要耗费大量的时间。那么为什么当插入和删除时,就要移动大量的元素?根据线性表的顺序存储结构的定义,其中的数据元素是存放在一段地址连续的存储空间中的,所以相邻两元素的存储位置也是相邻的,简单的说就是它们都是挨着的,我们要插入必须要移动大量元素。因为线性表的顺序存储结构的这个缺点,线性表的链式存储结构就出现了,下面我们看下它的定义:
链式存储结构是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的。数据元素的存储关系不能反映其逻辑关系,因此需要一个指针存放数据元素的地址,通过这个地址就可以找到相关联数据元素的位置。
为了表示每个数据元素ai与其直接后继数据元素ai+₁之间的逻辑关系,对数据元素ai来说,除了存储其本身的信息之外,还需要存储一个指示其直接后继的信息(即直接后继的存储位置)。我们把存储数据元素信息的域称为数据域,把存储直接后继位置的域称为指针域。指针域中存储的信息称作指针或链,这两部分信息组成数据元素ai的存储映像,称为结点。
n个结点链接成一个链表,即为线性表的链式存储结构,因为此链表的每个结点中只包含一个指针域,所以叫做单链表。
我们把链表中第一个结点的存储位置叫做头指针,整个链表的存取必须是从头指针开始进行。同时我们规定,线性表的最后一个结点指针为空(通常用NULL或“^”符号表示)。
有时,我们为了更加方便地对链表进行操作,会在单链表的第一个结点前附设一个结点,称为头结点。头结点的数据域可以不存储任何信息,也可以存储如线性表的长度等附加信息,头结点的指针域存储指向第一个结点的指针。以下是头指针和头结点的异同:
| 头指针 | 头结点 |
|---|---|
| 头指针是指链表指向第一个结点的指针,若链表有头结点,则是指向头结点的指针 | 头结点是为了操作的统一和方便而设立的,放在第一元素的结点之前,其数据域一般无意义(也可存放链表长度) |
| 头指针具有标识作用,所以常用头指针冠以链表的名字 | 有了头结点,对在第一元素结点前插入节点和删除第一结点,其操作与其它结点的操作就统一了 |
| 无论链表是否为空,头指针均不为空。头指针是链表的必要元素 | 头结点不一定是链表必要要素 |
单链表中,我们在C语言中可用结构指针来描述。
//线性表的单链表存储结构
typedef struct Node{
//数据域
ElemType data;
//指针域,指向直接后继数据元素地址
struct Node *next;
}Node;
//定义LinkList
typedef struct Node *LinkList;
单链表的读取、插入和删除
-
单链表中数据元素的读取
由于单链表并不是使用连续的地址来存储数据元素,因此我们无法像线性表的顺序存储结构那样方便的获取到任意一个元素的存储位置。在单链表中要获得链表第i个数据的算法思路:
(1)声明一个指针p指向链表第一个结点,初始化j从1开始。
(2)当j < i时,就遍历链表,让p的指针向后移动,不断指向下一结点,j累加。
(3)若到链表末尾p为空,则说明第i个结点不存在。
(4)否则查找成功,返回结点p的数据。实现代码算法如下:
//初始条件:单链表L已存在,1<=i<=ListLength(L) //操作结果:用e返回L中第i个数据元素的值 Status GetElem(LinkList L,int i,ElemType *e){ int j; //声明一指针p LinkList p; //让p指向链表L的第一个结点 p = L->next; //j为计数器 j = 1; //p不为空且计数器j还没有等于i时,循环继续 while(p && j < i){ //让p指向下一个结点 p = p->next; ++j; } if(!p || j > i){ //第i个结点不存在 return ERROR; } //取第i个结点的数据。结果就保存在e中 *e = p->data; return OK; } -
单链表的插入
单链表第i个数据插入结点的算法思路:
(1)声明一指针p指向链表头结点,初始化j从1开始
(2)当j < i时,就遍历链表,让p的指针向后移动,不断指向下一结点,j累加1
(3)若链表末尾p为空,则说明第i个结点不存在
(4)否则查找成功,在系统中生成一个空结点s
(5)将数据元素e赋值给s->data
(6)单链表的插入标准语句s->next=p->next; p->next = s;
(7)返回成功实现代码算法如下:
//时间复杂度为O(n) //初始条件:单链表L已存在,1<=i<=ListLength(L) //操作结果:在L中第i个结点位置之前插入新的数据元素e,L的长度加1 Status ListInsert(LinkList *L,int i,ElemType e){ int j; LinkList p,s; p = *L; j = 1; //寻找第i-1个结点 while(p && j < i){ p = p->next; ++j; } if(!p || j > i){ //第i个结点不存在 return ERROR; } //生成新结点 s = (LinkList)malloc(sizeof(Node)); //将p的后置结点的地址赋值给s的指针域 s->next=p->next; //将s的地址赋给p的指针域 p->next = s; return OK; } -
单链表的删除
单链表第i个数据删除结点的算法思路:
(1)声明一指针p指向链表头指针,初始化j从1开始
(2)当j < i时,就遍历链表,让p的指针向后移动,不断指向下一结点,j累加1
(3)若链表末尾p为空,则说明第i个结点不存在
(4)否则查找成功,将欲删除的结点p->next赋值给q
(5)单链表的删除标准语句p->next=q->next;
(6)将q节点中的数据赋值给e,作为返回。
(7)释放q结点
(8)返回成功实现代码算法如下:
//时间复杂度为O(n)
//初始条件:单链表L已存在,1<=i<=ListLength(L)
//操作结果:删除L中第i个结点,并用e返回其值,L的长度减1
Status ListDelete(LinkList *L,int i,ElemType *e){
int j;
LinkList p,q;
p = *L;
j = 1;
//寻找第i-1个结点
while(p->next && j < i){
p = p->next;
++j;
}
if(!(p->next) || j > i){
//第i个结点不存在
return ERROR;
}
q = p->next;
//将q的后继赋值给p的后继
p->next=q->next;
//将q结点中的数据给e
*e = q->data;
//让系统回收此结点,释放内存
free(q);
return OK;
}
从整个算法来看,如果在我们不知道第i个结点的指针位置,单链表数据结构在插入和删除操作上,与线性表的顺序存储结构是没有太大优势的。但如果,我们希望从第i个位置,插入10个结点,对于顺序存储结构意味着,每一次插入都需要移动n-i个结点,每次都是O(n)。而单链表,我们只需要在第一次时,找到第i个位置的指针,此时为O(n),接下来只是简单地通过赋值移动指针而已,时间复杂度为O(1)。显然,对于插入和删除数据越频繁的操作,单链表的效率优势就越是明显。
单链表的整表创建
顺序存储结构的创建,其实就是一个数组的初始化,即声明一个类型和大小的数组并赋值的过程。而单链表和顺序存储结构就不一样,它不像顺序存储结构这么集中,它可以很散,是一种动态结构。对于每个链表来说,它所占用空间的大小和位置是不需要预先分配划定的,可以根据系统的情况和实际的需求即时生成。所以创建单链表的过程就是一个动态生成链表的过程,即从空表的初始状态起,依次建立各元素结点,并逐个插入链表。
单链表整表创建的算法思路:
- 声明一指针p和计数器变量i
- 初始化一空链表L
- 让L的头结点的指针指向NULL,即建立一个带头结点的单链表
- 循环:
- 生成一新结点赋值给p
- 随机生成一数字赋值给p的数据域p->data
- 将p插入到头结点与前一新结点之间(头插法)
实现代码算法如下:
//随机产生n个元素的值,建立带表头结点的单链线性表L(头插法--始终让新结点在第一的位置)
void CreateListHead(LinkList *L,int n){
LinkList p;
int i;
//初始化随机数种子
srand(time(0));
//先建立一个带头结点的单链表
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL;
for(i = 0; i < n; i++){
//生成新结点
p = (LinkList)malloc(sizeof(Node));
//随机生成100以内的数字
p->data = rand()%100+1;
//将p的指针域置为NULL
p->next = (*L)->next;
//插入到表头,即头结点指向新结点
(*L)->next = p;
}
}
当然除了头插法,还有尾插法,尾插法的实现代码如下:
//随机产生n个元素的值,建立带表头结点的单链线性表L(尾插法--把每次新结点都插在终端结点的后面)
void CreateListHead(LinkList *L,int n){
LinkList p,r;
int i;
//初始化随机数种子
srand(time(0));
//新建单链表
*L = (LinkList)malloc(sizeof(Node));
//r为指向尾部的结点
r = *L;
for(i = 0; i < n; i++){
//生成新结点
p = (Node*)malloc(sizeof(Node));
//随机生成100以内的数字
p->data = rand()%100+1;
//将表尾终端结点的指针指向新结点
r->next = p;
//将当前新结点定义为表尾终端结点
r = p;
}
//表示当前链表结束
r->next = NULL;
}
单链表的整表删除
当我们不打算使用这个链表时,我们需要把它销毁,其实也就是在内存中将它释放掉。单链表整表删除的算法思路如下:
- 声明结点p和q
- 将第一个结点赋值给p
- 循环:
- 将下一结点赋值给q
- 释放p
- 将q赋值给p
实现代码算法如下:
//初始条件:顺序线性表L已存在,操作结果:将L重置为空表
Status ClearList(LinkList *L){
LinkList p,q;
p = (*L)->next;
while(p){
q = p->next;
free(p);
p = q;
}
//头结点指针域为空
(*L)->next = NULL;
return OK;
}
单链表结构与顺序存储结构优缺点
| 存储分配方式 | 时间性能 | 空间性能 |
|---|---|---|
| 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素 ; 单链表采用链式存储结构,用一组任意的存储单元存放线性表的元素 | 1.查找时间复杂度:顺序存储结构O(1); 单链表O(n) 2.插入和删除:顺序存储结构需要平均移动表长一半的元素,时间复杂度为O(n); 单链表在得出某位置的指针后,插入和删除时间仅为O(1) | 顺序存储结构需要预分配存储空间,分大了,浪费,分小了易发生上溢; 单链表不需要预分配存储空间,只要有就可以分配,元素个数也不受限制 |
通过上面的对比,我们可以得出一些结论:
- 若线性表需要频繁查找,很少进行插入和删除操作时,宜采用顺序存储结构。若需要频繁插入和删除时,宜采用单链表结构。
- 当线性表中的元素个数变化较大或者根本不知道多大时,最好用单链表结构,这样就可以不需要考虑存储空间的大小问题。而如果事先知道线性表的大致长度,比如一年12个月,一周就是周一至周日共七天,这种用顺序存储结构效率会高很多
静态链表(游标实现法–不具备指针语言的实现)
C语言具有指针能力,使得它可以非常容易地操作内存中的地址和数据,那对于那些没有指针的高级语言要如何实现单链表呢?答案是数组。用数组来代替指针,来描述单链表,这就是静态链表。具体是如何实现的呢?
首先我们让数组的元素都是由两个数据域组成,data和cur。数据域data用来存放数据元素,也就是通常我们要处理的数据;cur相当于单链表中的next指针,存放该元素的后继在数组中的下标,简称游标。
线性表的静态链表存储结构代码实现:
//假设链表的最大长度为1000.为了方便插入数据,我们通常会把数组建立的大一些,以便有一些空闲空间可以便于插入时不至于溢出
#define MAXSIZE 1000
typedef struct{
ElemType data;
//游标,为0时表示无指向
int cur;
}Component,StaticLinkList[MAXSIZE];
另外我们对数组第一个和最后一个元素作为特殊元素处理,不存数据。我们通常把未被使用的数组元素称为备用链表。而数组第一个元素,即下标为0的元素的cur就存放备用链表的第一个结点的下标(即第一个未被使用的数组元素的下标);而数组的最后一个元素的cur则存放第一个有数值的元素的下标,相当于单链表的头结点的作用,当整个链表为空时,则为0。
下面是初始化数组的状态的代码:
//将一维数组space中各分量链成一备用链表(备用链表:未被使用的数组元素)
//space[0].cur为头指针,“0”表示空指针
Status InitList(StaticLinkList space){
int i;
for(i = 0 ; i < MAXSIZE - 1 ; i++){
//初始化状态,每一个元素的cur指向下一个坐标(第一个元素和最后一个元素除外)
space[i].cur = i+1;
}
//目前静态链表为空,最后一个元素的cur为0
space[MAXSIZE-1].cur = 0;
return OK;
}
-
静态链表的插入操作
为了辨明数组中哪些分量未被使用,解决的办法是将所有未被使用过的及已被删除的分量用游标链成一个备用链表(上一面初始化的时候其实已经完成),每当进行插入时,便可以从备用链表上取得第一个结点作为待插入的新结点。获取插入结点的下标的实现代码算法如下:
//若备用空间链表非空,则返回分配的结点下标,否则返回0 int Malloc_SLL(StaticLinkList space){ //当前数组第一个元素的cur存的值就是要返回的第一个备用空闲的下标 int i = space[0].cur; //非0为true if(space[0].cur){ //由于要拿出一个分量来使用,所以我们就得把它的下一个分量拿来备用 space[0] = space[i].cur; } return i; }静态链表插入数据元素的算法思路如下:
(1)判断插入的位序是否符合规范,不符合返回ERROR
(2)获得空闲分量的下标,如果空闲分量下标为0,说明已满无法继续插入,返回ERROR
(3)若空闲分量下标不为0,将插入数据赋值给此分量的data
(4)找到插入位序i之前的位置,比如插入位序为3,则之前的位置为2
(5)把第i个元素之前的cur赋值给新元素(插入数据)的cur,并把新元素(插入数据)的下标赋值给第i个元素之前元素的cur。在上一步我们获取到之前的位置为2,其cur为3,假设我们要在静态链表位序为3(注意,这里是静态链表意义上的3,在数组中其下标不一定为3)的位置插入数据,此时我们就设置空闲分量处的cur为3,然后原来2上面的cur设置为空闲分量的下标
(6)返回成功下面是插入数据的代码算法实现:
//在L中第i个元素之前插入新的数据元素 Status LinkInsert(StaticLinkList L,int i,ElemType e){ int j,k,l; //注意k首先是最后一个元素的下标 k = MAXSIZE - 1; //如果插入位置异常,直接返回ERROR if(i < 1 || i > ListLength(L) + 1){ return ERROR; } //获得空闲分量的下标 j = Malloc_SSL(L); if(j){ //将数据赋值给此分量data L[j].data = e; //找到第i个元素之前的位置 for(l = 1; l <= i - 1; l++ ){ k = L[k].cur; } //把第i个元素之前的cur赋值给新的元素的cur L[j].cur = L[k].cur; //把新元素的下标赋值给第i个元素之前元素的cur L[k].cur = j; return OK; } return ERROR; } -
静态链表的删除操作
静态链表删除数据元素的算法思路如下:
(1)判断删除的位序是否符合规范,不符合返回ERROR
(2)找到第i个元素之前的位置
(3)获取到要删除元素所在位置的下标
(4)将要删除要素的cur赋值给第i个元素之前元素的cur
(5)释放空间
(6)返回成功下面是删除数据的代码算法实现:
//删除在L中第i个数据元素e Status ListDelete(StaticLinkList L,int i){ int j,k; //如果删除位置异常,直接返回ERROR if(i < 1 || i > ListLength(L)){ return ERROR; } //注意k首先是最后一个元素的下标 k = MAXSIZE - 1; //找到第i个元素之前的位置 for(j = 1; j <= i - 1; j++ ){ k = L[k].cur; } //获取到要删除元素所在位置的下标 j = L[k].cur; //将要删除要素的cur赋值给第i个元素之前元素的cur L[k].cur = L[j].cur; //释放空间 Free_SSL(L,j) return OK; }下面是释放空间,即回收结点到备用链表的代码实现:
void Free_SSL(StaicLinkList space,int k){
//把第一个元素cur值赋值给要删除的分量cur
space[k].cur = space[0].cur;
//把要删除的分量下标赋值给第一个元素的cur
space[0].cur = k;
}
当然静态链表也有相应的其他操作的相关实现。可以根据自己需求去实现。
静态链表的优缺点
优点:
- 在插入和删除操作时,只需要修改游标,不需要移动元素,从而改进了在顺序存储结构中插入和删除操作需要移动大量元素的缺点
缺点:
- 没有解决连续存储分配带来的表长难以确定的问题
- 失去了顺序存储结构随机存取的特性,即随机存取的时间复杂度不再是O(1)。因为当前读取一个数据元素,需要通过遍历来读取,而不是之前的直接通过计算就可以
循环链表
当我们需要从单链表中间的某个结点出发,访问到链表的全部结点,该如何操作呢?答案是循环链表。
循环链表:将单链表中终端结点的指针端由空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表就称为单循环链表,简称循环链表。
在单链表中,我们有了头结点时,我们可以用O(1)的时间访问第一个结点,但对于要访问到最后一个结点,却需要O(n),因为我们需要将单链表全部扫描一遍。但是如果我们采用尾指针(指向终端结点的指针为尾指针),就可以实现用O(1)的时间访问到最后一个结点。
双向链表
我们在单链表中,有了next指针,这就使得我们要查找下一结点的时间复杂度为O(1)。可如果我们要查找的是上一结点的话,那最坏的时间复杂度就是O(n)了,因为我们每次都要从头开始遍历查找。
为了克服单向性这一缺点,提出了双向链表的概念:**双向链表是在单链表的每个结点中,再设置一个指向其前驱结点的指针域。**所以在双向链表中的结点都有两个指针域,一个指向直接后继,另一个指向直接前驱。下面是双向链表的结构:
typedef struct DulNode{
ElemType data;
//直接前驱指针
struct DulNode *prior;
//直接后继指针
struct DulNode *next;
}DulNode,*DuLinkList;