Is Levenberg-Marquardt the Most Efficient Optimization Algorithm for Implementing Bundle Adjustment?
LM算法是执行BA的最有效的优化算法吗?
Lourakis M I A , Argyros A A . Is Levenberg-Marquardt the Most Efficient Optimization Algorithm for Implementing Bundle Adjustment?[C]// 10th IEEE International Conference on Computer Vision (ICCV 2005), 17-20 October 2005, Beijing, China. IEEE, 2005.
Abstract
为了获得最佳的3D结构(3D structure) 和观察参数(viewing parameter) 估计,BA通常被用作基于特征的结构和运动估计算法(structure and motion estimation) 的最后一步。BA涉及大规模但稀疏的最小化问题的制定(formulation),传统上使用Levenberg-Marquardt优化算法的稀疏变体解决该问题,该算法避免在零条目(entries)上存储和操作。本文认为,通过用稀疏版的Powell狗腿非线性最小二乘技术(the sparse variant of Powell’s dog leg non-linear least squares technique) 代替稀疏版的Levenberg-Marquardt算法来实现束调整,可以获得可观的计算效益。详细的比较实验结果提供了支持该主张的有力证据。
1. Introduction
捆绑调整(Buddle Adjustment, BA) 通常用作许多基于特征的3D重建算法(3D reconstruction algorithms) 的最后一步; 例如,参见[6,1,5,19,12]的一些代表性方法。排除特征跟踪,BA通常是在3D重建算法中产生的最耗时的计算。BA相当于(amounts to)一个大规模优化问题【该问题的解决是通过同时优化3D结构和观察参数(即,相机位姿和内参标定)】,以获得一个重建【该重建在某些假设下关于与观察到的图像特征有关的噪声是最优的】。如果图像误差是零均值高斯,则BA是ML估计器。 在文献[21]中给出了关于BA方法的优秀概述。
BA归结为最小化观察到的和预测的图像点(the observed and predicted image points) 之间的重投影误差,其表示为大量非线性实值函数的平方和。因此,使用非线性最小二乘算法实现最小化,其中Levenberg-Marquardt(LM)由于其相对容易实现而变得非常流行,且LM算法使用有效的阻尼策略,使其能够从广泛的初始猜测(a wide range of initial guesses) 中迅速收敛。通过在当前估计的邻域中迭代地线性化待最小化的函数,LM算法涉及称为正规方程(the normal equations) 的线性系统的解。当解决BA中出现的最小化问题时,由于不同3D点和相机的参数之间缺乏相互作用(the lack of interaction among parameters for different 3D points and cameras) ,正规方程矩阵具有稀疏块结构。因此,实现可观的计算收益的直接方法是 通过开发LM算法的定制的稀疏变体来实现BA(该算法明确地利用了正规方程中的零模式)[8]。
然而,除了利用稀疏性之外,很少有关于加速BA的研究已经发表。特别是,LM算法是大多数BA实现的事实标准(the de facto standard)[7]。本文认为Powell的狗腿(DL)算法[20]优于LM,因为它也可以从稀疏实现中受益,同时对大规模问题具有相当低的计算要求。本文的其余部分安排如下。 为了完整起见,第2节和第3节提供了用于解决非线性最小二乘问题的LM和DL算法的简短教程介绍。第4节讨论了DL相对于LM的性能优势。 第5节提供了基于LM和DL的BA之间的实验比较,它清楚地证明了后者在执行时间方面的优越性。 本文最后将在第6节进行简要讨论。
2. Levenberg-Marquardt’s Algorithm
LM算法是一种迭代技术,它定位多元函数的局部最小值【该函数表示为几个非线性实值函数的平方和】。它已成为非线性最小二乘问题的标准技术,在各种学科中广泛采用,用于处理数据拟合应用。LM可以被认为是最速下降和高斯 - 牛顿方法的组合。若当前解决方案远离局部最小值时,算法表现得像最速下降方法:缓慢但保证收敛。若当前解接近局部最小值时,它变为高斯 - 牛顿方法并且表现出快速收敛。为了帮助读者复现第4节中进行的LM和DL之间的比较,接下来提供了基于[13]中材料的LM算法的简短描述。但请注意,对LM算法的详细分析超出了本文的范围,感兴趣的读者可参考[18,13,9]进行更广泛的了解。
3. The Dog Leg Algorithm
与LM算法类似,(用于无约束最小化的)DL算法尝试将高斯 - 牛顿和最速下降方向的组合。然而,在DL算法中,通过使用信任域(trust region) 的方式明确地控制了这种组合(this is explicitly controlled via the use of trust region)。在过去的几十年中,信赖域方法已经得到了研究,并已经产生了可靠且稳健的数值算法,具有强收敛性,且甚至适用于不适应的问题(ill-conditioned problems)[2]。在信任区域框架中,关于目标函数(the objective function) f f f 的信息被收集起来,并用于构造一个二次模型函数(a quadratic model function) L L L,该模型函数的行为在当前点附近的与目标函数的行为类似。在以当前点为中心以 Δ \Delta Δ为半径的超球内的点,模型函数被信任能够精确代表目标函数,因此称为信任域。然后通过(近似地)使信赖区域上的模型函数 L L L最小化来找到最小化目标函数 f f f的新候选步(a new candidate step)。模型函数被选择为二次曲线,即对应于等式(2)等号右半部分的平方项:
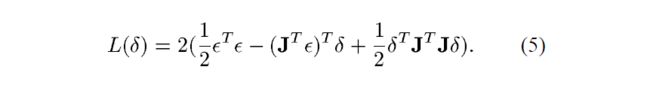
通过上述定义,候选步是下述带约束子问题的解:

显然,信任域的半径对于候选步的成功至关重要。如果该区域太大,则该模型函数可能不是目标函数的良好近似,因此,模型函数的最小值可能远离该区域中的目标函数的最小值。另一方面,如果区域太小,则计算得到的候选步骤使当前点接近目标函数的最小值得程度不够充分(the computed candidate step might not suffice to bring the current point closer to the minimizer of the objective function)。在实践中,信赖域半径得选择是基于:在先前迭代期间,模型函数近似目标函数的成功(程度、次数?)。如果模型函数是可靠的,即准确地预测了目标函数的行为,则增加半径以允许测试更长的步骤。如果模型函数未能预测当前信任区域上的目标函数,则之后的半径(the radius of the latter) 减小并且再次求解(6),这次求解是在更小的信任区域上。
信赖域子问题(6)的解【是一个信任域半径的函数】是如图2所示的曲线。在一篇开创性的论文中,Powell [20]提出用一条由两条线段组成的分段线性轨迹逼近该曲线。第一段从当前点到Cauchy点,由沿最陡下降方向的目标函数的无约束最小值定义,即:
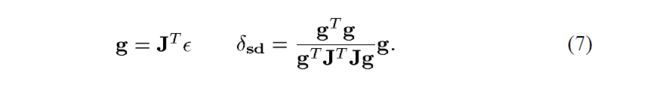
第二个线段从 δ s d \delta_{sd} δsd到Gauss-Newton步 δ g n \delta_{gn} δgn,后者为方程(3)的解:
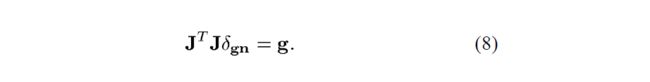
由于矩阵偶尔会变成正半定,方程(8)借助于扰动Cholesky分解(perturned Cholesky decomposition) 来解决,这确保了正定性[4]。正式地,狗腿轨迹被定义为:
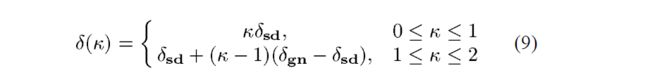
文献[4]表明, δ ( κ ) \delta(\kappa) δ(κ)的长度是 κ \kappa κ的一个单调递增函数(a monotonically increasing function) ,并且表明,模型函数关于 δ ( κ ) \delta(\kappa) δ(κ)的值是 κ \kappa κ的一个单调递减函数(a monotonically decreasing function)。此外,Cauchy步(the Cauchy step) 总是比Gauss-Newton步短。 考虑到上述事实,狗腿步(the dog leg step) 定义如下:如果柯西点位于信任域之外,则狗腿步被选择为截断的柯西步(the truncates cauchy step),即柯西步与信信任域边界的交点 Δ ∥ δ s d ∥ δ s d \frac{\Delta}{\|\delta_{sd}\|}\delta_{sd} ∥δsd∥Δδsd。否则,否则,如果Gauss-Newton步在信任域内,则狗腿步被取值等于它。最后,当Cauchy点在信赖域之内且Gauss-Newton步在信任域之外时,下一个尝试点(the next trial point) 被计算为信任域边界与连接Cauchy点和Gauss-Newton步的直线的交点(见图2)。在所有情况下,狗腿路径(the dog leg path) 最多与信任域边界相交一次,且交叉点可以解析地确定(无需搜索)。图3给出了DL算法的伪代码描述,且在文献[4,13]中可以找到更多相关细节。刚刚描述的策略也被称为单狗腿(the single dog leg),以区别于Dennis和Mei 在文献[3]中提出的双狗腿(the double dog leg) 。双狗腿是Powell的原始算法的一个略微修改版,其引入了朝向高斯 - 牛顿方向的偏差,已经观察到(证实)该偏差导致更好的性能。用户定义参数的指示值(indicative values) 是 Δ 0 = 1.0 , ε 1 = ε 2 = 1 0 − 12 , k m a x = 100 \Delta_0=1.0,\varepsilon_1=\varepsilon_2=10^{-12},k_{max}=100 Δ0=1.0,ε1=ε2=10−12,kmax=100。

在这一点上,应该提到增强正规方程(the argmented noraml equation)(4)和(6)的解之间存在密切关系。…
4. DL vs. LM: Performance Issues
我们现在可以对LM和DL算法的计算力需求(the computational requirements) 进行定性比较(a qualiative comparison)。当LM步失效时,LM算法要求再次求解由增加的阻尼项产生的增强方程。换句话说,对阻尼项的每次更新都需要一次增强方程的新解,因此失败的步骤意味着无产出的努力(unproductive effort)。与此相反,一旦确定了Gauss-Newton步长,DL算法就可以对许多个 Δ \Delta Δ的值求解方程(6)对应的约束二次子问题,而无需再求解方程(8)。还要注意,当采用截断的Cauchy步时,DL算法可以避免求解方程(8)但LM算法却总是需要求解方程(4),即使选择小于Cauchy步。对于最小化过程的整体性能而言,减少方程(8)的求解次数是至关重要的,因为BA问题涉及许多参数,因此,线性代数运算(linear algebra) 和图1、3两种算法中相关的每一次内部迭代,占了主要的计算开销。由于上述原因,就计算力需求方面而言,DL算法是BA中出现的非线性最小化的更有希望的实现。
