如何找到字符串中的最长回文子串？

作者 | channingbreeze

责编 | 胡巍巍

小史是一个应届生，虽然学的是电子专业，但是自己业余时间看了很多互联网与编程方面的书，一心想进BAT互联网公司。可是努力了很久，别说BAT了，连TMD的橄榄枝都没有接到。

可是他越挫越勇。这不，今天他又去一家互联网小巨头公司面试了。

面试现场

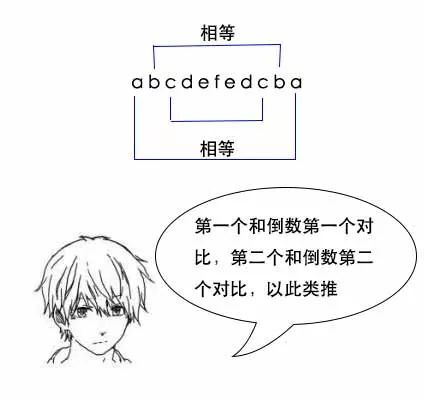
小史：只要先对比第一个字符和倒数第一个字符，再对比第二个字符和倒数第二个字符，以此类推。如果都相等，那就是回文串了。

题目：给你一个字符串，找出里面最长的回文子串。

例如，输入abcdcef，那么输出应该是cdc；

输入adaelele，输出应该是elele。

半分钟过去了。

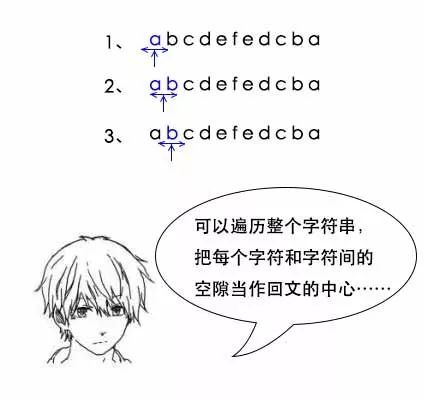
小史：可以遍历整个字符串，把每个字符和字符间的空隙当作回文的中心，然后向两边扩展来找到最长回文串。小史这次抢着分析时间和空间复杂度。

一分钟过去了。

请教大神

小史回到学校，把面试情况和吕老师说了一下。

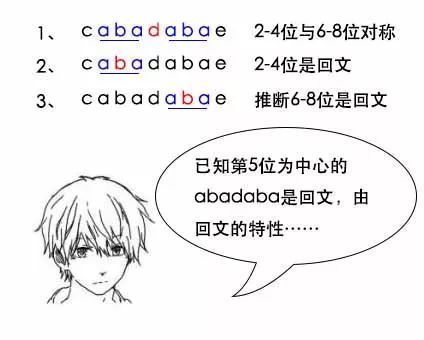
吕老师：比如cabadabae用中心扩展的算法，我已经知道了第三位为中心的aba和第5位为中心的abadaba是回文，那么在判断第7位为中心的回文串的时候，有什么已知信息吗？

小史：已知第5位为中心的abadaba是回文，由回文的特性，就能够知道2-4位和6-8位对称，而又知道第3位为中心的aba是回文，所以2-4位是回文。这样的话，6-8位肯定是回文。

小史拿着笔在纸上画了半天，突然大叫一声。

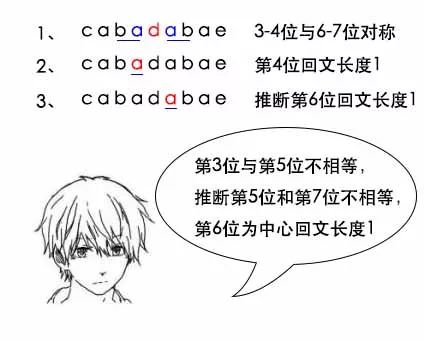
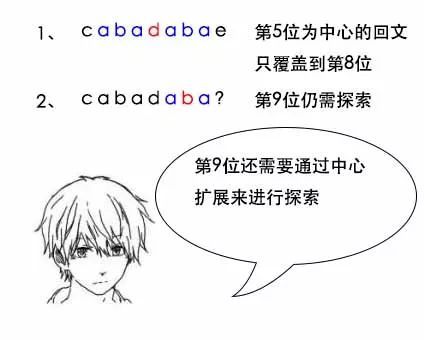
小史：由于之前的计算，已经知道了第5位为中心的abadaba是回文，而第4位为中心的a的回文长度是1，所以第6位为中心的回文长度只能是1，不用再去扩展判断了。

小史：以第7位为中心的回文串的计算，由之前分析已经知道最小长度是3了，但是还是需要进行扩展，因为第9位是什么，根据之前的信息无法得知，需要扩展进行探索。

小史：而以第6位为中心的回文串的计算，并不需要进行探索了，因为根据之前第5位为回文中心串的信息、和第4位为回文中心串的信息，已经可以推断，第6位为回文中心串的长度只能为1。

小史：当然可以。

1、首先，我们要记录下目前已知的回文串能够覆盖到的最右边的地方，就像案例中的第8位

2、同时，覆盖到最右边的回文串所对应的回文中心也要记录，就像案例中的第5位

3、以每一位为中心的回文串的长度也要记录，后面进行推断的时候能用到，就像案例中用到的以第3位为中心的回文和第4位为中心的回文

4、对于新的中心，我们判断它是否在右边界内，若在，就计算它相对右边界回文中心的对称位置，从而得到一些信息，同时，如果该中心需要进行扩展，则继续扩展就行。

编码实现

小史：回文的中心有可能是两个字符中间，这种情况没有考虑到啊。

小史：

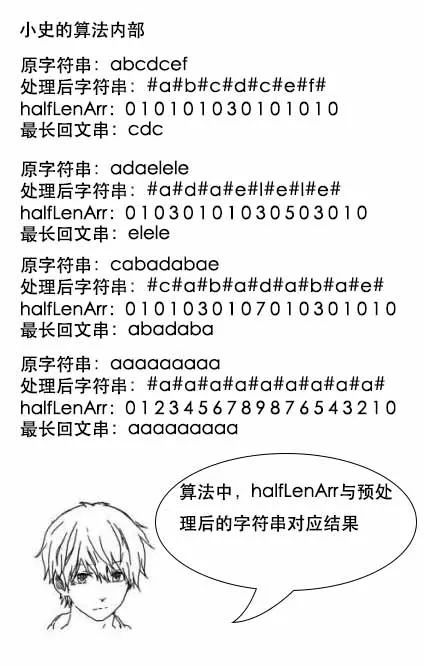
1、先对字符串进行预处理，两个字符之间加上特殊符号#；

2、然后遍历整个字符串，用一个数组来记录以该字符为中心的回文长度，为了方便计算右边界，我在数组中记录长度的一半（向下取整）；

3、每一次遍历的时候，如果该字符在已知回文串最右边界的覆盖下，那么就计算其相对最右边界回文串中心对称的位置，得出已知回文串的长度；

4、判断该长度和右边界，如果达到了右边界，那么需要进行中心扩展探索。当然，如果第3步该字符没有在最右边界的“羽翼”下，则直接进行中心扩展探索。进行中心扩展探索的时候，同时又更新右边界；

5、最后得到最长回文之后，去掉其中的特殊符号即可。

理解了算法之后，小史的代码写起来也是非常快，不一会儿就写好了：

PlalindromeString.java：

/**
 * @author xiaoshi on 2018/9/24.
 * Happy Mid-Autumn Festival
 */
public class PlalindromeString {

    // 判断一个字符串是否回文，算法中用不到了
    @Deprecated
    private boolean isPlalindrome(String s) {
        int len = s.length();
        for(int i = 0; i < len / 2; i++) {
            if(s.charAt(i) != s.charAt(len - 1 - i)) {
                return false;
            }
        }
        return true;
    }

    // 预处理字符串，在两个字符之间加上#
    private String preHandleString(String s) {
        StringBuffer sb = new StringBuffer();
        int len = s.length();
        sb.append('#');
        for(int i = 0; i < len; i++) {
            sb.append(s.charAt(i));
            sb.append('#');
        }
        return sb.toString();
    }

    // 寻找最长回文字串
    public String findLongestPlalindromeString(String s) {
        // 先预处理字符串
        String str = preHandleString(s);
        // 处理后的字串长度
        int len = str.length();
        // 右边界
        int rightSide = 0;
        // 右边界对应的回文串中心
        int rightSideCenter = 0;
        // 保存以每个字符为中心的回文长度一半（向下取整）
        int[] halfLenArr = new int[len];
        // 记录回文中心
        int center = 0;
        // 记录最长回文长度
        int longestHalf = 0;
        for(int i = 0; i < len; i++) {
            // 是否需要中心扩展
            boolean needCalc = true;
            // 如果在右边界的覆盖之内
            if(rightSide > i) {
                // 计算相对rightSideCenter的对称位置
                int leftCenter = 2 * rightSideCenter - i;
                // 根据回文性质得到的结论
                halfLenArr[i] = halfLenArr[leftCenter];
                // 如果超过了右边界，进行调整
                if(i + halfLenArr[i] > rightSide) {
                    halfLenArr[i] = rightSide - i;
                }
                // 如果根据已知条件计算得出的最长回文小于右边界，则不需要扩展了
                if(i + halfLenArr[leftCenter] < rightSide) {
                    // 直接推出结论
                    needCalc = false;
                }
            }
            // 中心扩展
            if(needCalc) {
                while(i - 1 - halfLenArr[i] >= 0 && i + 1 + halfLenArr[i] < len) {
                    if(str.charAt(i + 1 + halfLenArr[i]) == str.charAt(i - 1 - halfLenArr[i])) {
                        halfLenArr[i]++;
                    } else {
                        break;
                    }
                }
                // 更新右边界及中心
                rightSide = i + halfLenArr[i];
                rightSideCenter = i;
                // 记录最长回文串
                if(halfLenArr[i] > longestHalf) {
                    center = i;
                    longestHalf = halfLenArr[i];
                }
            }
        }
        // 去掉之前添加的#
        StringBuffer sb = new StringBuffer();
        for(int i = center - longestHalf + 1; i <= center + longestHalf; i += 2) {
            sb.append(str.charAt(i));
        }
        return sb.toString();
    }

}

Main.java：

/**
 * @author lixin on 2018/9/24.
 */
public class Main {

    public static void main(String[] args) {

        PlalindromeString ps = new PlalindromeString();

        String[] testStrArr = new String[] {
            "abcdcef",
            "adaelele",
            "cabadabae",
            "aaaabcdefgfedcbaa",
            "aaba",
            "aaaaaaaaa"
        };

        for(String str : testStrArr) {
            System.out.println(String.format("原字串 : %s", str));
            System.out.println(String.format("最长回文串 : %s", ps.findLongestPlalindromeString(str)));
            System.out.println();
        }

    }

}

运行结果：

原字串 : abcdcef
最长回文串 : cdc

原字串 : adaelele
最长回文串 : elele

原字串 : cabadabae
最长回文串 : abadaba

原字串 : aaaabcdefgfedcbaa
最长回文串 : aabcdefgfedcbaa

原字串 : aaba
最长回文串 : aba

原字串 : aaaaaaaaa
最长回文串 : aaaaaaaaa

时间空间分析

作者简介：channingbreeze，国内某互联网公司全栈开发。

声明：本文为作者投稿，版权归对方所有。作者独立观点，不代表 CSDN 立场。

苹果手机的微信改版了，

想快速看到CSDN的热乎文章，

赶快把CSDN公众号设为星标吧，

打开公众号，点击“设为星标”就可以啦！

安卓手机的用户，

点击公众号右上角小人，就可以置顶啦。

_“ 征稿啦_”

CSDN 公众号秉持着「与千万技术人共成长」理念，不仅以「极客头条」、「畅言」栏目在第一时间以技术人的独特视角描述技术人关心的行业焦点事件，更有「技术头条」专栏，深度解读行业内的热门技术与场景应用，让所有的开发者紧跟技术潮流，保持警醒的技术嗅觉，对行业趋势、技术有更为全面的认知。

如果你有优质的文章，或是行业热点事件、技术趋势的真知灼见，或是深度的应用实践、场景方案等的新见解，欢迎联系 CSDN 投稿，联系方式：微信（guorui_1118，请备注投稿+姓名+公司职位），邮箱（[email protected]）。

推荐阅读：

• 如何快速构建一个 Spring Boot 工程？
  

• 国庆通知：地球不爆炸，CSDN 不放假！
  

• Python 爬虫告诉你，国庆这几个景点千万别去！
  

• 男神不老, 基努里维斯老伙计拍了首部区块链大电影, 还没上映就燃爆了社交媒体 | 假期荐片

• 程序员最大黑幕：1.5w代面试，承诺入职顶级公司！

• 假期快乐！超强面试资源等你Pick，先收藏！

• 引战：Java 的开发效率究竟比 C++ 高在哪里？