LSH搜索算法

LSH(Location Sensitive Hash),即位置敏感哈希函数。与一般哈希函数不同的是位置敏感性，也就是散列前的相似点经过哈希之后，也能够在一定程度上相似，并且具有一定的概率保证。

作者注：LSH算法分两种：SimHash和MinHash。

simhash的原理是减少搜索空间，用汉明距离替代余弦距离

minHash的原理是降维。通过hash映射函数，将特征元素的个数降下来。

形式化定义：

对于任意q,p属于S，若从集合S到U的函数族H={h1,h2...hn}对距离函数D(,)，如欧式距离、曼哈顿距离等等，满足条件：

 

则称D(,)是位置敏感的。

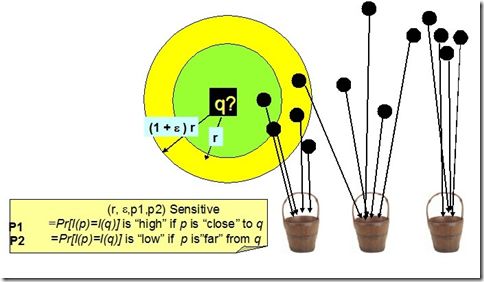
如下图，空间上的点经位置敏感哈希函数散列之后，对于q，其rNN有可能散列到同一个桶（如第一个桶）,即散列到第一个桶的概率较大，会大于某一个概率阈值p1;而其(1+emxilong)rNN之外的对象则不太可能散列到第一个桶，即散列到第一个桶的概率很小，会小于某个阈值p2.

LSH的作用

◆高维下近似查询

相似性检索在各种领域特别是在视频、音频、图像、文本等含有丰富特征信息领域中的应用变得越来越重要。丰富的特征信息一般用高维向量表示，由此相似性检索一般通过K近邻或近似近邻查询来实现。一个理想的相似性检索一般需要满足以下四个条件：

1. 高准确性。即返回的结果和线性查找的结果接近。

2. 空间复杂度低。即占用内存空间少。理想状态下，空间复杂度随数据集呈线性增长，但不会远大于数据集的大小。

3. 时间复杂度低。检索的时间复杂度最好为O（1）或O（logN)。

4. 支持高维度。能够较灵活地支持高维数据的检索。

传统主要方法是基于空间划分的算法——tree类似算法，如R-tree，Kd-tree，SR-tree。这种算法返回的结果是精确的，但是这种算法在高维数据集上的时间效率并不高。实验[1]指出维度高于10之后，基于空间划分的算法时间复杂度反而不如线性查找。LSH方法能够在保证一定程度上的准确性的前提下，时间和空间复杂度得到降低，并且能够很好地支持高维数据的检索。

◆分类和聚类

根据LSH的特性，即可将相近（相似）的对象散列到同一个桶之中，则可以对图像、音视频、文本等丰富的高维数据进行分类或聚类。

◆数据压缩。如广泛地应用于信号处理及数据压缩等领域的Vector Quantization量子化技术。

总而言之，哪儿需要近似kNN查询，哪儿都能用上LSH.

LSH搜索算法

对于一个查询点q以及给定的距离阈值r，搜索桶g1(q),...,gL(q)，取出其中的所有点v1,...,vn作为候选近似最近邻点。对于任意的vj，如果D(q,vj)<=r，那么返回vj，其中D为相似性度量函数。
在创建LSH索引时,选取的哈希函数是k个LSH函数的串联函数,这样就相对拉大了距离近的点冲突的概率pn与距离远的点冲突的概率pf之间的差值,但这同时也使这两个值一起减小了,于是需要同时使用L张哈希表来加大pn同时减小pf。通过这样的构造过程,在查询时,与查询点q距离近的点就有很大的概率被取出作为候选近似最近邻点并进行最后的距离计算,而与查询点q距离远的点被当作候选近似最近邻点的概率则很小,从而能够在很短的时间内完成查询。

LSH是由文献[1]提出的一种用于高效求解最近邻搜索问题的Hash算法。LSH算法的基本思想是利用一个hash函数把集合中的元素映射成hash值，使得相似度越高的元素hash值相等的概率也越高。LSH算法使用的关键是针对某一种相似度计算方法，找到一个具有以上描述特性的hash函数。LSH所要求的hash函数的准确数学定义比较复杂，以下给出一种通俗的定义方式：

对于集合S，集合内元素间相似度的计算公式为sim(*,*)。如果存在一个hash函数h(*)满足以下条件：存在一个相似度s到概率p的单调递增映射关系，使得S中的任意两个满足sim(a,b)>=s的元素a和b，h(a)=h(b)的概率大于等于p。那么h(*)就是该集合的一个LSH算法hash函数。

一般来说在最近邻搜索中，元素间的关系可以用相似度或者距离来衡量。如果用距离来衡量，那么距离一般与相似度之间存在单调递减的关系。以上描述如果使用距离来替代相似度需要在单调关系上做适当修改。

根据元素相似度计算方式的不同，LSH有许多不同的hash算法。两种比较常见的hash算法是随机投影法和min-hash算法。本文即将介绍的随机投影法适用于集合元素可以表示成向量的形式，并且相似度计算是基于向量之间夹角的应用场景，如余弦相似度。min-hash法在参考文献[2]中有相关介绍。

2 随机投影法(Random projection)

假设集合S中的每个元素都是一个n维的向量：

v⃗ ={v1,v2,…,vn}

，集合中两个元素 v⃗  和 u⃗  之间的相似度定义为

sim(v⃗ ,u⃗ )=v⃗ ∗u⃗ |v⃗ ||u⃗ |

。

对于以上元素集合S的随机投影法hash函数h(*)可以定义为如下：

在n维空间中随机选取一个非零向量x⃗ ={x1,x2,…,xn}。考虑以该向量为法向量且经过坐标系原点的超平面，该超平面把整个n维空间分成了两部分，将法向量所在的空间称为正空间，另一空间为负空间。那么集合S中位于正空间的向量元素hash值为1，位于负空间的向量元素hash值为0。判断向量属于哪部分空间的一种简单办法是判断向量与法向量之间的夹角为锐角还是钝角，因此具体的定义公式可以写为

h(v⃗ )={1,0,v⃗ ∗x⃗ >0v⃗ ∗x⃗ <=0

。

根据以上定义，假设向量v⃗ 和u⃗ 之间的夹角为θ，由于法向量x⃗ 是随机选取的，那么这两个向量未被该超平面分割到两侧（即hash值相等）的概率应该为：p(θ)=1−θπ。假设两个向量的相似度值为s，那么根据θ=arccos(s),有

p(s)=1−arccos(s)π

。因此，存在相似度s到概率p的单调递增映射关系，使得对于任意相似度大于等于s的两个元素，它们hash值相等的概率大于等于 p(s) 。所以，以上定义的hash值计算方法符合LSH算法的要求。

以上所描述的h(*)函数虽然符合LSH算法的要求，但是实用性不高。因为该hash函数只产生了两个hash值，没有达到hash函数将元素分散到多个分组的目的。为了增加不同hash值的个数，可以多次生成独立的函数h(*)，只有当两个元素的多个h(*)值都相等时才算拥有相同的hash值。根据该思路可以定义如下的hash函数H(*)：

H(v⃗ )=(hb(v⃗ )hb−1(v⃗ )…h1(v⃗ ))2

。其中每个 hi(v⃗ ) 表示一个独立的h(*)函数，H(*)函数值的二进制表现形式中每一位都是一个h(*)函数的结果。

以H(*)为hash函数的话，两个相似度为s的元素具有相同hash值的概率公式为

p(s)=(1−arccos(s)π)b

。hash值的个数为 2b 。很容易看出H(*)函数同样也是符合LSH算法要求的。一般随机按投影算法选用的hash函数就是H(*)。其中参数b的取值会在后面小节中讨论。

3 随机投影法在最近邻搜索中的应用

3.1 最近邻搜索

最近邻搜索可以简单的定义为：对于m个元素的集合T，为一个待查询元素q找到集合中相似度最高的k个元素。

最近邻搜索最简单的实现方法为：计算q与集合T中每一个元素的相似度，使用一个具有k个元素的大顶堆（优先队列）保存相似度计算结果（相似度值为key）。这种实现方法每一次查询都要遍历整个集合T来计算相似度，当m很大并且查询的频率很高的时候这种暴力搜索的方法无法满足性能要求。

当最近邻搜索的近邻要求并不是那么严格的时候，即允许top k近邻的召回率不一定为1（但是越高越好），那么可以考虑借助于LSH算法。

3.2 随机投影法提高执行速度

这里我们介绍当集合T的元素和查询元素q为同维度向量(维度为n)，并且元素相似度计算方法为余弦相似度时，使用随机投影法来提高最近邻搜索的执行速度。具体的实现方法为：

预处理阶段：使用hash函数H(*)计算集合T中所有元素的hash值，将集合T分成一个个分组，每个分组内的元素hash值均相等。用合适的数据结构保存这些hash值到分组的映射关系（如HashMap）。

查询阶段：计算查询元素q的hash值H(q)，取集合T中所有hash值为H(q)的分组，以该分组内的所有元素作为候选集合，在候选该集合内使用简单的最近邻搜索方法寻找最相似的k个元素。

该方法的执行效率取决于H(*)的hash值个数2b，也就是分组的个数。理想情况下，如果集合T中的向量元素在空间中分布的足够均匀，那么每一个hash值对应的元素集合大小大致为m2b。当m远大于向量元素的维度时，每次查询的速度可以提高到2b倍。

根据以上分析H(*)中b的取值越大算法的执行速度的提升越多，并且是指数级别的提升。但是，在这种情况下H(*)函数下的概率公式p(s)，实际上表示与查询元素q的相似度为s的元素的召回率。当b的取值越大时，top k元素的召回率必然会下降。因此算法执行速度的提升需要召回率的下降作为代价。例如：当b等于10时，如果要保证某个元素的召回率不小于0.9，那么该元素与查询元素q的相似度必须不小于0.9999998。

3.3 提高召回率改进

为了在保证召回率的前提下尽可能提高算法的执行效率，一般可以进行如下改进：

预处理阶段：生成t个独立的hash函数Hi(∗)，根据这t个不同的hash函数，对集合T进行t种不同的分组，每一种分组方式下，同一个分组的元素在对应hash函数下具有相同的hash值。用合适的数据结构保存这些映射关系（如使用t个HashMap来保存）。

查询阶段：对于每一个hash函数Hi(∗)，计算查询元素q的hash值Hi(q)，将集合T中Hi(∗)所对应的分组方式下hash值为Hi(q)的分组添加到该次查询的候选集合中。然后，在该候选集合内使用简单的最近邻搜索方法寻找最相似的k个元素。

以上改进使得集合中元素与查询元素q的t个hash值中，只要任意一个相等，那么该集合元素就会被加入到候选集中。那么，相似度为s的元素的召回率为

p(s)=1−(1−(1−arccos(s)π)b)t

在执行效率上，预处理阶段由于需要计算t个hash函数的值，所以执行时间上升为t倍。查询阶段，如果单纯考虑候选集合大小对执行效率的影响，在最坏的情况下，t个hash值获得的列表均不相同，候选集集合大小的期望值为t∗m2b，查询速度下降至1t，与简单近邻搜索相比查询速度提升为2bt倍。

下图是召回率公式p(s)=1−(1−(1−arccos(s)π)b)t在不同的b和t取值下的s-p曲线。我们通过这些曲线来分析这里引入参数t的意义。4条蓝色的线以及最右边红色的线表示当t取值为1（相当于没有引入t），而b的取值从1变化到5的过程，从图中可以看出随着b的增大，不同相似度下的召回率都下降的非常厉害，特别的，当相似度接近1时曲线的斜率很大，也就说在高相似度的区域，召回率对相似度的变化非常敏感。10条红色的线从右到左表示b的取值为5不变，t的取值从1到10的过程，从图中可以看出，随着t的增大，曲线的形状发生了变化，高相似度区域的召回率变得下降的非常平缓，而最陡峭的地方渐渐的被移动到相对较低的相似度区域。因此，从以上曲线的变化特点可以看出，引入适当的参数t使得高相似度区域在一段较大的范围内仍然能够保持很高的召回率从而满足实际应用的需求。

3.4 参数选取

根据以上分析，H(*)函数的参数b越大查询效率越高，但是召回率越低；参数t越大查询效率越低但是召回率越高。因此选择适当参数b和t来折中查询效率与召回率之间的矛盾是应用好随机投影法的关键。下面提供一种在实际应用中选取b和t的参考方法。

根据实际应用的需要确定一对(s,p)，表示相似度大于等于s的元素，召回率的最低要求为p。然后将召回率公式表示成b-t之间的函数关系t=log1−(1−acos(s)pi)b(1−p)。根据(s,p)的取值，画出b-t的关系曲线。如s=0.8,p=0.95时的b-t曲线如下图所示。考虑具体应用中的实际情况，在该曲线上选取一组使得执行效率可以达到最优的(b,t)组合。

3.5 关于最近邻文本搜索

在最近邻文本搜索中，一般待检索的文本或查询文本，都已被解析成一系列带有权重的关键词，然后通过余弦相似度公式计算两个文本之间的相似度。这种应用场景下的最近邻搜索与以上所提到的最近邻搜索问题相比存在以下两个特点：

• 如果把每个文本的带权重关键词表都看作是一个向量元素的话，每个关键词都是向量的一个维度，关键词权重为该维度的值。理论上可能关键词的个数并不确定（所有单词的组合都可能是一个关键词），因此该向量元素的维数实际上是不确定的。
• 由于关键词权重肯定是大于零的，所以向量元素的每一个维度的值都是非负的。

对于第一个特点，我们需要选取一个包含n个关键词的关键词集合，在进行文本相似度计算时只考虑属于该集合的关键词。也就是说，每一个文本都视为是一个n维度的向量，关键词权重体现为对应维度的值。该关键词集合可以有很多种生成办法，比如可以是网站上具有一定搜索频率的关键词集合，总的来说该关键词集合应当能够涵盖所有有意义并且具有一定使用频率的关键词。通常n的取值会比较大，如几十万到几百万，由于在使用随机投影算法时，每一个生成的随机向量维度都为n，这种情况下需要特别考虑利用这些高维随机向量对执行效率造成的影响，在确定b、t参数时需要考虑到这方面的影响。

对于第二个特点，由于向量元素各维度值都非负，那么这些元素在高维空间中只会出现在特定的区域中。比如当n为3时，只会出现在第一象限中。一个直观的感觉是在生成随机向量的时候，会不会生成大量的无用切割平面（与第一个象限空间不相交，使得所有元素都位于切割平面的同侧）。这些切割平面对应的H(*)函数hash值中的二进制位恒定为1或者0，对于提高算法执行速度没有帮助。以下说明这种担心是没有必要的：

切割平面与第一象限空间不相交等价于其法向量的每一个维度值都有相同的符号（都为正或者负），否则总能在第一象限空间中找到两个向量与法向量的乘积符号不同，也就是在切割平面的两侧。那么，随机生成的n维向量所有维度值都同号的概率为12n−1，当n的取值很大时，该概率可以忽略不计。

后部分链接：http://blog.csdn.net/wejoncy/article/details/49150495

1 Jaccard相似度

    Jaccard相似度计算十分便于计算离散集合之间的相似度，在个性化推荐中应用极广。Jaccard的相似度计算如图1所示，其中S和T的相似度为J(S,T)=3/8。

图1 Jaccard相似度计算

    PS：大量连续的相似度计算，也可以转成Jaccard相似度计算，在此不述。

2 Simhash

    Simhash主要做用是使复杂度o(nml)中，使m<

    Simhash是通过设计一个hash方法，使要内容相近item生的hash签名也相近，hash签名的相近程度，也能反映出item间的相似程度。

    Simhash算法如下：

假设item={item1,item2,…}，取hash函数，将item的每一个元素hash成一个M位的int签名值，将int值按二进制表示，0处全表示为-1，记为H，将所有按位相加，最后加正的位为1，为负的位值为0，这就是item最后的simhash结果。这样就可以使相似的item有相近的hash值。

    举例说明如下，假设item a ={1,2,3,4}, item b={1,2,3,5}, h(x)=x%8，M=3，有如图2中的结果，item a的sim hash值为(0,0,1,0)，item b的sim hash值为(0,0,1,1)，可见两者的sim hash值相似,通过两者的汉明码计算，便可以用汉明码来衡量两者的相似程度。

图2 simhash计算

    从降维的脚度看，通过将item预处理为simhash值后，通过计算两者的汉明距离计算相似度。可惜汉明距离并不能完全表征两者的实际相似程度，因而simhash常用于缩小搜索空间，计算item a的top M相似item时，搜索限为汉明距离最近的空间中。例如假设hash在64位，共将有2⁶⁴个hash桶，将所有item预先按hash桶建好索引后，计算item a的top M或满足某域值的相似item时，可从最近的hash桶中搜索，最近的桶为本桶中的其它item，其次为1位不同的其它hash桶，共64个，再次为2位不同的桶，共64*64个…

3 Minhash  

    Minhash主要做用是使复杂度o(nml)中，使l<

    由第1节可知，计算J(S,T)的关键在于计算S∩T或S∪T。直接求S∩T或S∪T，在有序的归并方法中，复杂度也是k的级别。Minhash的目的是降维，主要原理是两集合经随机转换后得到的两个最小hash值相等的概率等于两集合的Jaccard的相似度！(可以枚举出相应结果)。

     由于只取一个hash函数时，只有相等与不等两个结果，对应于原理，也就只有相似与不相似不个结果。取一系列hash函数后，便可以概率性地统计出结果，而取hash函数的个数据，决定将k降维后的维数l，l越大，相似结果与实际相似度越相近，一般10个左右就已经能满足工程需求。

     这样数据预处理完后，计算两item间的复杂度，就等于计算最小Minhash相同的概率了。

    PS：在工程中，不容易找一系列的hash函数，由hash母函数生成的一系列hash函数可能相关，将降低Minhash的经度。

4 优势与局限性

    Simhash和Minhash都有明显的应用局限性：

1、集合中的item要比较多；

2、所求的相关项要比较相似；

    优势：

1、简化复杂相似项计算；

2、原理易于理解，点破后，给人显而易见的感觉。

转载部分的链接：http://blog.csdn.net/pi9nc/article/details/12250361