官方题解:
最小K路径覆盖的模型,用费用流或者KM算法解决,构造二部图,X部有N*M个节点,源点向X部每个节点连一条边,流量1,费用0,Y部有N*M个节点,每个节点向汇点连一条边,流量1,费用0,如果X部的节点x可以在一步之内到达Y部的节点y,那么就连边x->y,费用为从x格子到y格子的花费能量减去得到的能量,流量1,再在X部增加一个新的节点,表示可以从任意节点出发K次,源点向其连边,费用0,流量K,这个点向Y部每个点连边,费用0,流量1,最这个图跑最小费用最大流,如果满流就是存在解,反之不存在,最小费用的相反数就是可以获得的最大能量
个人理解:
昨儿在比赛时大致看了下这题,也想到了网络流,但是由于题意没理解清楚,并且个人太菜,没能想到正确的方法。
对于官方的题解,很简单的表述,但是要理解透却没那么容易(特别对于我这种菜鸟)。经过吃饭、走路时间的思考,终于略有感触,下面谈谈我的理解吧。
我画了这张图:
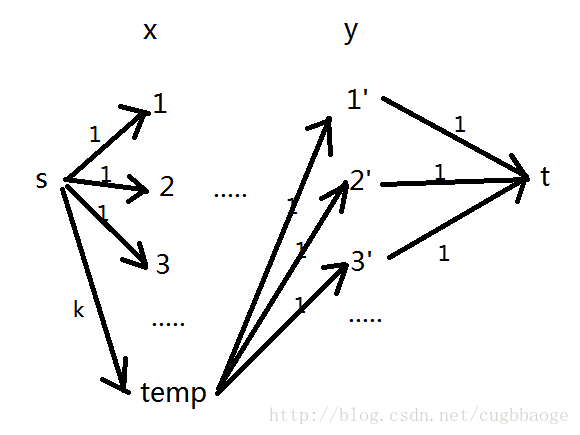
为什么建在x集再建一个点就好了呢?首先我们可以想想没有这个点的情况,那么y集一些点到t会有流量,这些点是作为跳的终点能到达的点,而y集到t没有流量的那些点就必须是作为起点到达了,所以在x集加一个点给它k的流量,如果这样能满留,就说明起点数量在k个以内,就符合条件了。
一开始,我想能不能不加这个点而是判断它的流量是不是达到了m*n-k,但后来观察前三组样例,实践+思考后,发现这个是不行的,想一想不难发现,费用流求解过程中是优先流量大,其次才是保证费用的最值,这里的满留在题中的含义就是能遍历全图,如果不加这个点,它也是优先流量大,因而会单纯为了流量大而取到较小的cost值,从而得到较小的错误答案。
理解了这个,相信离A题也不远了,之后就是费用流的方法即可。
为了改善自己的代码风格,我的代码参考白书(训练指南),希望自己以后不要因为恶劣的代码风格浪费大量debug时间了。
#include
#include
#include
#include
#include
#include
