【谈谈知识点】BST（无指针）

前言

联赛完了之后废了好长一段时间啊……甚至忘记了我有博客了~
不过再怎么说还是要时常上来写一写东西的嘛
另外博主不会不喜欢用指针，所以所有的代码都是数组版。

有人问我：为什么要写BST这种东西，平时做题的时候根本用不到（因为复杂度炸妈
但我觉得，很多平衡树是在此基础上出现的
所以从这里开始，可以方便的理解各个操作，过渡到平衡树应该也容易一点~

Update 2019-3-14
这篇代码貌似问题很大。。我自己当时随手打的都没去尝试下可行性。。烦请各位等我明天更新QAQ

Update 2019-3-15
确保了代码的可行性，（且与splay格式相近）。
（尽管我找不到BST的模板题，只能在平衡树那边找了几组简单数据）

1.What is BST?

二叉搜索树（binary search tree），缩写为BST，具有以下性质：

1.所有非叶子结点至多拥有两个儿子（Left和Right）；

2.所有结点存储一个关键字；

3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

就比如这个：

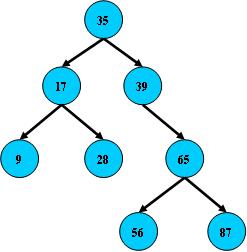
用通俗易懂的话讲，这是颗二叉树，且对于每个节点，其左子树的所有节点的权值都小于它，其右子树的所有节点的权值都大于它。

那么一种数据结构肯定对应一类问题啦！SO：

2.What can be solved？

想象一下，有这样一类维护区间信息的题，要求支持以下操作：

1、插入一个数
2、删除一个数
3、查询某个数x在区间内的排名
4、查询排名为x的数是什么
5、查询某个数x的前驱
6、查询某个数x的后继

传送门：【模板】普通平衡树

当然如果你把数据离散化一下，然后用权值线段树离线也可以x过去 强制在线

所以有没有什么想法？（疯狂暗示）

对，这东西拿BST做就非常方便了！

2.0 一些约定

博主的码风可能有些鬼畜 ，所以先把某些定义说清楚：

先考虑下，这棵树的每个节点存啥呢？

首先需要左儿子，右儿子，父亲，该节点的值( son[2]，fa，val）

然后为了节约空间记一个重复标记代表有几个这个数 (num)

然后还需要一个size统计以该节点为根（包括这个节点）的树里有多少个值

（个别题还需要统计子树和之类的东西，这里就不写了）

具体说来就是这样：

struct Node{
    int son[2],fa,val,num,size;
//  son[0]为左儿子，son[1]为右儿子，num是重复标记。
	ivoid create(int x,int f){val=x;fa=f;num=size=1;son[0]=son[1]=0;}
//  新建节点用：赋值为x，其父亲为f
}t[N<<2];

然后我(们)还有几个常用的函数：

iint side(int x)//返回1或0，表示x是它父亲的哪个儿子。
{return t[t[x].fa].son[1]==x;}

ivoid update(int x)//统计该节点为根的树有多少个值
{t[x].size=t[x].num+t[t[x].son[0]].size+t[t[x].son[1]].size;}

ivoid connect(int x,int y,int side)//让x成为y的son[side]
{t[x].fa=y;t[y].son[side]=x;}

2.1 插入

由于我们要时刻维护这颗树的性质，所以插入的时候需要注意：

1、首先是找到这个节点该放在哪里。如果当前节点的值比他小，我们往右走，反之我们往左走。

当然再考虑一下特殊情况，如果这个值已经出现过了，我们把标记++即可。

2、如果这个值之前没有出现过，那么最终肯定会出现n=0的情况，此时我们需要新建节点。此时要记得把新增的节点和它的父节点连起来，否则访问和统计都会出问题。

ivoid insert(int val,int fa,int n)
{//顺带说一句：写成Insert的话，以后写树套树就不会跟线段树的Build重复了（对我而言
	if(!n){
        t[++cnt].create(val,fa);
        connect(cnt,fa,val>t[fa].val);
        if(n==rt)rt=cnt;
        //这一步是为了在上为空时，让第一个插入的点成为根
        //否则rt一直都是0
        return;
	}
    t[n].size++;
	if(t[n].val==val){t[n].num++;return;}
	if(t[n].val>val)insert(val,n,t[n].son[0]);
	else insert(val,n,t[n].son[1]);
}

2.2 查找某个数对应的节点编号

这个功能题目里没要求，不过实现很简单，跟插入的时候是一样的，后面也可用于辅助其他功能。
具体实现这里就不细讲了，相信大家一看就懂。

iint find(int val,int n)
{
    if(!n)return -1;
    if(t[n].val==val)return n;
    if(t[n].val>val)return find(val,t[n].son[0]);
    else return find(val,t[n].son[1]);
}

2.3 前驱&后继

BST的优点$\times$ 1，查找前驱和后继非常的方便，在2.2 find 的基础上加一点点就可以了。

由于两者的查找方式相似，我们就只讨论前驱：

1、当前节点的值或大于给定值，那么我们往左子树走，因为右子树的值都比当前点更大。

2、当前节点的值小于给定值，那么我们记录这个点，然后往右子树走。
原因也很简单：当前节点的左子树肯定没有我们想要的答案了（都小于当前节点，不比当前节点优），那么如果还有更优的答案，肯定在右子树了；如果没有，那当前记录的答案就是最优答案。

后继就同理啦~

iint find_pre(int val,int n,int ans)
{
    if(!n)return ans;//把 ans 改成 t[ans].val 就是返回值了
    if(t[n].val>=val)return find_pre(val,t[n].son[0],ans);
    else return find_pre(val,t[n].son[1],n);
}

iint find_suf(int val,int n,int ans)
{
    if(!n)return ans;
    if(t[n].val<=val)return find_suf(val,t[n].son[1],ans);
    else return find_suf(val,t[n].son[0],n);
}

2.4 删除

为了维护性质，我们不能直接删除。那么我们分情况讨论：

1、要删除的节点是叶节点，由于它没有儿子，所以直接删了就行。
2、要删除的节点只有一个儿子，此时我们让这个儿子代替原来的节点
3、要删除的节点有两个儿子，那么这下就比较麻烦了，我们又要分三步进行：

①我们需要找到x的前驱对应的节点编号pos，也就是在左子树里找到最大值。

②交换pos节点和x节点的值（交换后除了这两个点，其他的仍满足性质，因为是相邻的嘛）

③删除pos节点

另外提一句，这里的删除都可以通过改变归属关系实现，并不需要把节点的值都赋值为0。

ivoid crash(int val)
{
    int n=find(val,rt);
    if(!n)return;
    if(t[n].num>1){t[n].num--;return;}
    if(!t[n].son[0]&&!t[n].son[1]){t[t[n].fa].son[side(n)]=0;return;}
    if(!t[n].son[0]||!t[n].son[1]){
    	if(n==rt)rt=0;//避免树空时可能出现的错误
    	t[t[n].son[0]+t[n].son[1]].fa=t[n].fa;
        t[t[n].fa].son[side(n)]=t[n].son[0]+t[n].son[1];
        return;
    }
   int pos=find_pre(t[n].val,n,0);
   //这里的find_pre返回的是编号
   swap(t[pos].val,t[n].val);
   t[t[pos].fa].son[side(pos)]=0;
}

2.5 用值查找排名

BST的优点$\times$ 2

(这里的排名是指从小往数)

首先明确，一个节点的排名是怎么来的。首先它的左子树都小于他，其次就是它的某些祖先节点和那些祖先节点的左子树。比如这个：

根据BST的性质，黑点的值一定都小于蓝点的值。由此，我们从根一直往下搜，每当我们往右子树走，就把左子树的size和当前节点的num累加起来，最后就能得到排名啦~

另外记住：千万别忘了在最后答案+1，因为蓝色点排名=黑色点个数+1。

iint val_rank(int val,int n,int ans)
{
    if(t[n].val==val)return ans+t[t[n].son[0]].size+1;
    if(t[n].val>val)return val_rank(val,t[n].son[0],ans);
    else return val_rank(val,t[n].son[1],ans+t[t[n].son[0]].size+t[n].num);
    //说真的这么长一串看着很烦，但又想不到好办法给他简化QAQ
}

2.6 用排名查找值

这个操作的思路有点像刚才的2.5 val_rank，也很像是权值线段树的操作，分为三种情况：

1、要查找的排名<左子树的size，那要找的值一定在左子树。

2、要查找的排名>(左子树的size+当前节点的num)，那要找的值一定在右子树，和权值线段树做法相同，要在查找的排名上-左子树size-当前节点num（不懂的话看代码，再画图理解一下）

3、如果前两种都不满足，那只可能是当前节点了，直接返回。

iint rank_val(int rank,int n)
{
    if(t[t[n].son[0]].size>rank)return rank_val(rank,t[n].son[0]);
    if(t[t[n].son[0]].size+t[n].num<rank)
    return rank_val(rank-t[t[n].son[0]].size-t[n].num,t[n].son[1]);
    return t[n].val;
}

至此题目要求的所有操作全部完美解决~
下面是无注释的全代码：

#include
#define rint register int
#define ivoid inline void
#define iint inline int
#define rint register int 
#define endll '\n'
using namespace std;
const int N=1e6+5;
int n,q,cnt,rt=0; 
struct Node{
    int son[2],fa,val,num,size;
	ivoid create(int x,int f){val=x;fa=f;num=size=1;son[0]=son[1]=0;}
}t[N];

iint rad()
{
	int x=0,f=1;char c;
	while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+c-'0',c=getchar();
	return x*f;
}

iint side(int x){return t[t[x].fa].son[1]==x;}
ivoid update(int x){t[x].size=t[x].num+t[t[x].son[0]].size+t[t[x].son[1].size;}
ivoid connect(int x,int y,int side){t[x].fa=y;t[y].son[side]=x;}

ivoid insert(int val,int fa,int n)
{
	if(!n){
        t[++cnt].create(val,fa);
        connect(cnt,fa,val>t[fa].val);
        if(n==rt)rt=cnt;
        return;
	}
    t[n].size++;
	if(t[n].val==val){t[n].num++;return;}
	if(t[n].val>val)insert(val,n,t[n].son[0]);
	else insert(val,n,t[n].son[1]);
}

iint find(int val,int n)
{
    if(!n)return -1;
    if(t[n].val==val)return n;
    if(t[n].val>val)return find(val,t[n].son[0]);
    else return find(val,t[n].son[1]);
}

iint find_pre(int val,int n,int ans)
{
    if(!n)return ans;
    if(t[n].val>=val)return find_pre(val,t[n].son[0],ans);
    else return find_pre(val,t[n].son[1],t[n].val);
}

iint find_suf(int val,int n,int ans)
{
    if(!n)return ans;
    if(t[n].val<=val)return find_suf(val,t[n].son[1],ans);
    else return find_suf(val,t[n].son[0],t[n].val);
}

ivoid crash(int val)
{
    int n=find(val,rt);
    if(!n)return;
    if(t[n].num>1){t[n].num--;return;}
    if(!t[n].son[0]&&!t[n].son[1]){t[t[n].fa].son[side(n)]=0;return;}
    if(!t[n].son[0]||!t[n].son[1]){
    	if(n==rt)rt=0;
    	t[t[n].son[0]+t[n].son[1]].fa=t[n].fa;
        t[t[n].fa].son[side(n)]=t[n].son[0]+t[n].son[1];
        return;
    }
   int pos=find_pre(t[n].val,n,0);
   swap(t[pos].val,t[n].val);
   t[t[pos].fa].son[side(pos)]=0;
}

iint val_rank(int val,int n,int ans)
{
    if(t[n].val==val)return ans+t[t[n].son[0]].size+1;
    if(t[n].val>val)return val_rank(val,t[n].son[0],ans);
    else return val_rank(val,t[n].son[1],ans+t[t[n].son[0]].size+t[n].num);
}

iint rank_val(int rank,int n)
{
    if(t[t[n].son[0]].size>rank)return rank_val(rank,t[n].son[0]);
    if(t[t[n].son[0]].size+t[n].num<rank)
    return rank_val(rank-t[t[n].son[0]].size-t[n].num,t[n].son[1]);
    return t[n].val;
}

int main()
{
    n=rad();
    while(n--){
    	q=rad();
    	if(q==1) insert(rad(),0,rt);
    	if(q==2) crash(rad());
    	if(q==3) cout<<val_rank(rad(),rt,0)<<endll;
    	if(q==4) cout<<rank_val(rad(),rt)<<endll;
    	if(q==5) cout<<find_pre(rad(),rt,0)<<endll;
    	if(q==6) cout<<find_suf(rad(),rt,0)<<endll;
    }
    return 0;
}

3.What can’t be solved?

二叉搜索树的基本功能已经介绍完毕。它的缺点非常明显：如果我们把有序的数列往里面进行插入，或者多插入些点，这棵树就会退化成一条链，这势必会导致效率的大幅降低（树形结构的log被去掉）。所以出题人稍微针对一下，这方法基本上就凉了~

但是在数据随机的情况下， BST的速度是居于所有平衡树之上的（这里第一篇题解的末尾部分看到的）。

当然，由于大部分平衡树都是在BST的基础上发展的，因而上述操作会出现在各大平衡树中也就不奇怪了。

至于平衡树嘛……博主看心情再更吧~（文化课爆炸不得不补）