完整的R语言预测建模实例-从数据清理到建模预测
概述
本文使用Kaggle上的一个公开数据集,从数据导入,清理整理一直介绍到最后数据多个算法建模,交叉验证以及多个预测模型的比较全过程,注重在实际数据建模过程中的实际问题和挑战,主要包括以下五个方面的挑战:
- 缺失值的挑战
- 异常值的挑战
- 不均衡分布的挑战
- (多重)共线性的挑战
- 预测因子的量纲差异
以上的几个主要挑战,对于熟悉机器学习的人来说,应该都是比较清楚的,这个案例中会涉及到五个挑战中的缺失值,量纲和共线性问题的挑战。
案例数据说明
本案例中的数据可以在下面的网址中下载:
https://www.kaggle.com/primaryobjects/voicegender/downloads/voicegender.zip
下载到本地后解压缩会生成voice.csv文件
下面首先大概了解一下我们要用来建模的数据
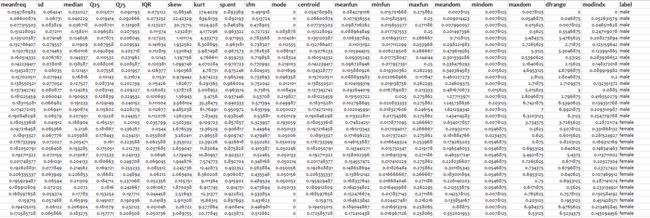
数据共包含21个变量,最后一个变量label是需要我们进行预测的变量,即性别是男或者女
前面20个变量都是我们的预测因子,每一个都是用来描述声音的量化属性。
下面我们开始我们的具体过程
步骤1:基本准备工作
步骤1主要包含以下三项工作:
- 设定工作目录
- 载入需要使用的包
- 准备好并行计算
-
### the first step: set your working directory
-
setwd(
"C:/Users/chn-fzj/Desktop/R Projects/Kaggle-Gender by Voice")
-
### R中的文件路径应把Windows系统默认的"\"替换为"/"
-
-
### load packages to be used, if not installed, please use ##install.packages("yourPackage")
-
require(readr)
-
require(ggplot2)
-
require(dplyr)
-
require(tidyr)
-
require(caret)
-
require(corrplot)
-
require(
Hmisc)
-
require(parallel)
-
require(doParallel)
-
require(ggthemes)
-
-
# parallel processing set up
-
n_Cores <- detectCores()
##检测你的电脑的CPU核数
-
cluster_Set <- makeCluster(n_Cores)
##进行集群
-
registerDoParallel(cluster_Set)
- 19
- 20
步骤2:数据的导入和理解
数据下载解压缩后就是一份名为‘voice.csv’ 的文件,我们将csv文件存到我们设定的工作目录之中,就可以导入数据了。
-
### read in original dataset
-
voice_Original <-
read_csv(
"voice.csv",col_names=TRUE)
-
describe(voice_Original)
- 1
- 2
- 3
- 1
- 2
- 3
Hmisc包中的describe 函数是我个人最喜欢的对数据集进行概述,整体上了解数据集的最好的一个函数,运行结果如下:
-
voice
_Original
-
-
21 Variables 3168 Observations
-
-------------------------------------------------------------------
-
meanfreq
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3166 1 0.1809 0.1260 0.1411 0.1637
-
.50 .75 .90 .95
-
0.1848 0.1991 0.2177 0.2291
-
-
lowest : 0
.03936 0
.04825 0
.05965 0
.05978 0
.06218
-
highest: 0.24353 0.24436 0.24704 0.24964 0.25112
-
-------------------------------------------------------------------
-
sd
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3166 1 0.05713 0.03162 0.03396 0.04195
-
.50 .75 .90 .95
-
0
.05916 0
.06702 0
.07966 0
.08549
-
-
lowest : 0
.01836 0
.02178 0
.02400 0
.02427 0
.02456
-
highest: 0.11126 0.11126 0.11265 0.11451 0.11527
-
-------------------------------------------------------------------
-
median
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3077 1 0.1856 0.1164 0.1340 0.1696
-
.50 .75 .90 .95
-
0.1900 0.2106 0.2274 0.2358
-
-
lowest : 0
.01097 0
.01359 0
.01579 0
.02699 0
.02936
-
highest: 0.25663 0.25698 0.25742 0.26054 0.26122
-
-------------------------------------------------------------------
-
Q25
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3103 1 0.1405 0.04358 0.07509 0.11109
-
.50 .75 .90 .95
-
0
.14029 0
.17594 0
.20063 0
.21524
-
-
lowest : 0
.0002288 0
.0002355 0
.0002395 0
.0002502 0
.0002669
-
highest: 0.2394595 0.2405416 0.2407352 0.2421235 0.2473469
-
-------------------------------------------------------------------
-
Q75
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3034 1 0.2248 0.1874 0.1963 0.2087
-
.50 .75 .90 .95
-
0.2257 0.2437 0.2536 0.2577
-
-
lowest : 0
.04295 0
.05827 0
.07596 0
.09019 0
.09267
-
highest: 0.26879 0.26892 0.26894 0.26985 0.27347
-
-------------------------------------------------------------------
-
IQR
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3073 1 0.08431 0.02549 0.02931 0.04256
-
.50 .75 .90 .95
-
0
.09428 0
.11418 0
.13284 0
.15632
-
-
lowest : 0
.01456 0
.01492 0
.01511 0
.01549 0
.01659
-
highest: 0.24530 0.24597 0.24819 0.24877 0.25223
-
-------------------------------------------------------------------
-
skew
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3166 1 3.14 1.123 1.299 1.650
-
.50 .75 .90 .95
-
2.197 2.932 3.916 6.918
-
-
lowest : 0
.1417 0
.2850 0
.3260 0
.5296 0
.5487
-
highest: 32.3507 33.1673 33.5663 34.5375 34.7255
-
-------------------------------------------------------------------
-
kurt
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3166 1 36.57 3.755 4.293 5.670
-
.50 .75 .90 .95
-
8.318 13.649 27.294 75.169
-
-
lowest : 2
.068 2
.210 2
.269 2
.293 2
.463
-
highest: 1128.535 1193.434 1202.685 1271.354 1309.613
-
-------------------------------------------------------------------
-
sp
.ent
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3166 1 0.8951 0.8168 0.8322 0.8618
-
.50 .75 .90 .95
-
0.9018 0.9287 0.9513 0.9630
-
-
lowest : 0
.7387 0
.7476 0
.7477 0
.7485 0
.7487
-
highest: 0.9764 0.9765 0.9765 0.9785 0.9820
-
-------------------------------------------------------------------
-
sfm
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3166 1 0.4082 0.1584 0.1883 0.2580
-
.50 .75 .90 .95
-
0.3963 0.5337 0.6713 0.7328
-
-
lowest : 0
.03688 0
.08024 0
.08096 0
.08220 0
.08266
-
highest: 0.82259 0.82267 0.82610 0.83135 0.84294
-
-------------------------------------------------------------------
-
mode
-
n missing unique Info Mean .05 .10 .25
-
3168 0 2825 1 0.1653 0.00000 0.01629 0.11802
-
.50 .75 .90 .95
-
0
.18660 0
.22110 0
.24901 0
.26081
-
-
lowest : 0
.0000000 0
.0007279 0
.0007749 0
.0008008 0
.0008427
-
highest: 0.2791181 0.2795230 0.2795852 0.2797034 0.2800000
-
-------------------------------------------------------------------
-
centroid
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3166 1 0.1809 0.1260 0.1411 0.1637
-
.50 .75 .90 .95
-
0.1848 0.1991 0.2177 0.2291
-
-
lowest : 0
.03936 0
.04825 0
.05965 0
.05978 0
.06218
-
highest: 0.24353 0.24436 0.24704 0.24964 0.25112
-
-------------------------------------------------------------------
-
meanfun
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3166 1 0.1428 0.09363 0.10160 0.11700
-
.50 .75 .90 .95
-
0
.14052 0
.16958 0
.18519 0
.19343
-
-
lowest : 0
.05557 0
.05705 0
.06097 0
.06254 0
.06348
-
highest: 0.22342 0.22576 0.22915 0.23114 0.23764
-
-------------------------------------------------------------------
-
minfun
-
n missing unique Info Mean .05 .10 .25
-
3168 0 913 1 0.0368 0.01579 0.01613 0.01822
-
.50 .75 .90 .95
-
0
.04611 0
.04790 0
.05054 0
.05644
-
-
lowest : 0
.009775 0
.009785 0
.009901 0
.009911 0
.010163
-
highest: 0.168421 0.178571 0.185185 0.200000 0.204082
-
-------------------------------------------------------------------
-
maxfun
-
n missing unique Info Mean .05 .10 .25
-
3168 0 123 0.99 0.2588 0.1925 0.2192 0.2540
-
.50 .75 .90 .95
-
0.2712 0.2775 0.2791 0.2791
-
-
lowest : 0
.1031 0
.1053 0
.1087 0
.1111 0
.1124
-
highest: 0.2774 0.2775 0.2778 0.2791 0.2791
-
-------------------------------------------------------------------
-
meandom
-
n missing unique Info Mean .05 .10 .25
-
3168 0 2999 1 0.8292 0.1045 0.1888 0.4198
-
.50 .75 .90 .95
-
0.7658 1.1772 1.5602 1.8004
-
-
lowest : 0
.007812 0
.007979 0
.007990 0
.008185 0
.008247
-
highest: 2.544271 2.591580 2.676989 2.805246 2.957682
-
-------------------------------------------------------------------
-
mindom
-
n missing unique Info Mean .05 .10
-
3168 0 77 0.92 0.05265 0.007812 0.007812
-
.25 .50 .75 .90 .95
-
0
.007812 0
.023438 0
.070312 0
.164062 0
.187500
-
-
lowest : 0
.004883 0
.007812 0
.014648 0
.015625 0
.019531
-
highest: 0.343750 0.351562 0.400391 0.449219 0.458984
-
-------------------------------------------------------------------
-
maxdom
-
n missing unique Info Mean .05 .10 .25
-
3168 0 1054 1 5.047 0.3125 0.6094 2.0703
-
.50 .75 .90 .95
-
4.9922 7.0078 9.4219 10.6406
-
-
lowest : 0
.007812 0
.015625 0
.023438 0
.054688 0
.070312
-
highest: 21.515625 21.562500 21.796875 21.843750 21.867188
-
-------------------------------------------------------------------
-
dfrange
-
n missing unique Info Mean .05 .10 .25
-
3168 0 1091 1 4.995 0.2656 0.5607 2.0449
-
.50 .75 .90 .95
-
4.9453 6.9922 9.3750 10.6090
-
-
lowest : 0
.000000 0
.007812 0
.015625 0
.019531 0
.024414
-
highest: 21.492188 21.539062 21.773438 21.820312 21.843750
-
-------------------------------------------------------------------
-
modindx
-
n missing unique Info Mean .05 .10 .25
-
3168 0 3079 1 0.1738 0.05775 0.07365 0.09977
-
.50 .75 .90 .95
-
0
.13936 0
.20918 0
.32436 0
.40552
-
-
lowest : 0
.00000 0
.01988 0
.02165 0
.02194 0
.02217
-
highest: 0.84448 0.85470 0.85776 0.87950 0.93237
-
-------------------------------------------------------------------
-
label
-
n missing unique
-
3168 0 2
-
-
female (1584, 50%), male (1584, 50%)
-
-------------------------------------------------------------------
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
通过这个函数,我们现在可以对数据集中的每一个变量都有一个整体性把握。
我们可以看出我们共有21个变量,共计3168个观测值。
由于本数据集数据完整,没有缺失值,因而我们实际上并没有缺失值的挑战,但是为了跟实际的数据挖掘过程相匹配,我们会人为将一些数据设置为缺失值,并对这些缺失值进行插补,大家也可以实际看一下我们应用的插补法的效果:
-
###missing values
-
##
set 30 numbers in the first column into NA
-
set.seed(1001)
-
random_Number <- sample(1:3168,30)
-
voice_Original1 <- voice_Original
-
voice_Original[random_Number,1] <- NA
-
describe(voice_Original)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 1
- 2
- 3
- 4
- 5
- 6
- 7
-
meanfreq
-
n
missing
unique
Info
Mean
.05
.10
.25
-
3138
30
3136
1
0.1808
0.1257
0.1411
0.1635
-
.50
.75
.90
.95
-
0.1848
0.1991
0.2176
0.2291
-
-
lowest :
0.03936
0.04825
0.05965
0.05978
0.06218
-
highest:
0.24353
0.24436
0.24704
0.24964
0.25112
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
这时候我们能看见,第一个变量meanfreq 中有了30个缺失值,现在我们需要对他们进行插补,我们会用到caret 包中的preProcess 函数
-
### impute missing data
-
original_Impute <- preProcess(voice_Original,
method="bagImpute")
-
voice_Original <-
predict
(original_Impute,voice_Original)
- 1
- 2
- 3
- 1
- 2
- 3
现在我们来看一下我们插补法的结果,我们的方法就是将我们设为缺失值的原始值和我们插补后的值结合到一个数据框中,大家可以进行直接比较:
-
### compare results of imputation
-
compare_Imputation <
-
data.frame(
-
voice_Original1
[
random_Number
,1],
-
voice_Original
[
random_Number
,1]
-
)
-
compare_Imputation
- 1
- 2
- 3
- 4
- 5
- 6
- 1
- 2
- 3
- 4
- 5
- 6
对比结果如下:
-
meanfreq
meanfreq
.1
-
1 0
.2122875 0
.2117257
-
2 0
.1826562 0
.1814900
-
3 0
.2009399 0
.1954627
-
4 0
.1838745 0
.1814900
-
5 0
.1906527 0
.1954627
-
6 0
.2319645 0
.2313031
-
7 0
.1736314 0
.1814900
-
8 0
.2243824 0
.2313031
-
9 0
.1957448 0
.1954627
-
10 0
.2159557 0
.2117257
-
11 0
.2047696 0
.2084277
-
12 0
.1831099 0
.1814900
-
13 0
.1873643 0
.1814900
-
14 0
.2077344 0
.2117257
-
15 0
.1648246 0
.1651041
-
16 0
.1885224 0
.1898701
-
17 0
.1342805 0
.1272604
-
18 0
.1933665 0
.1954627
-
19 0
.1888149 0
.1940667
-
20 0
.2180404 0
.2117257
-
21 0
.1980392 0
.1954627
-
22 0
.1898704 0
.1954627
-
23 0
.1761953 0
.1814900
-
24 0
.2356528 0
.2313031
-
25 0
.1785359 0
.1814900
-
26 0
.1856824 0
.1814900
-
27 0
.1808664 0
.1814900
-
28 0
.1784912 0
.1814900
-
29 0
.1990789 0
.1954627
-
30 0
.1714903 0
.1651041
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
可以看出,我们的插补出来的值和原始值之间的差异是比较小的,可以帮助我们进行下一步的建模工作。
另外一点,我们在实际工作中,我们用到的预测因子中,往往包含数值型和类别型的数据,但是我们数据中全部都是数值型的,所以我们要增加难度,将其中的一个因子转换为类别型数据,具体操作如下:
-
### add a categorcial variable
-
voice_Original <- voice_Original%>%
-
mutate(sp
.ent=
-
ifelse(sp
.ent>
0.9,
"High",
"Low"))
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
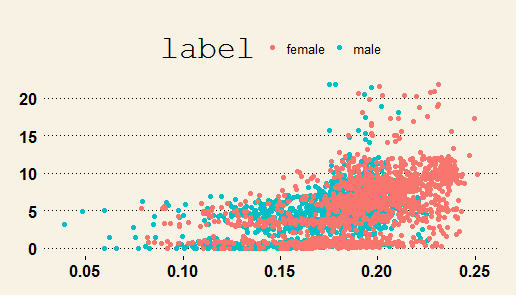
除了使用describe 函数掌握数据的基本状况外,一个必不可少的数据探索步骤,就是使用图形进行探索,我们这里只使用一个例子,帮助大家了解:
-
### visual exploration of the dataset
-
voice_Original%>%
-
ggplot(aes(x=meanfreq,y=dfrange))+
-
geom_point(aes(color=label))+
-
theme_wsj()
- 1
- 2
- 3
- 4
- 5
- 1
- 2
- 3
- 4
- 5
但是我们更关注的是,预测因子之间是不是存在高度的相关性,因为预测因子间的香瓜性对于一些模型,是有不利的影响的。
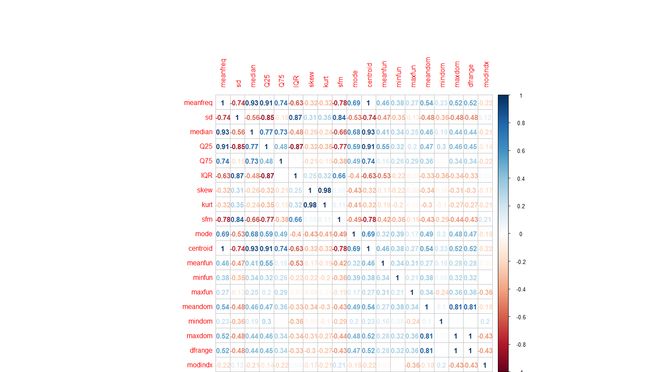
对于研究预测因子间的相关性,corrplot 包中的corrplot函数提供了很直观的图形方法:
-
###
find correlations between factors
-
factor_Corr <- cor(voice_Original[,-
c(
9,
21)])
-
corrplot(factor_Corr,
method="number")
- 1
- 2
- 3
- 1
- 2
- 3
这个相关性矩阵图可以直观地帮助我们发现因子间的强相关性。
步骤3:数据分配与建模
在实际建模过程中,我们不会将所有的数据全部用来进行训练模型,因为相比较模型数据集在训练中的表现,我们更关注模型在训练集,也就是我们的模型没有遇到的数据中的预测表现。
因此,我们将我们的数据集的70%的数据用来训练模型,剩余的30%用来检验模型预测的结果。
-
### separate dataset into training and testing sets
-
sample_Index <- createDataPartition(voice_Original
$label,p=
0.7,
list=
FALSE)
-
voice_Train <- voice_Original[sample_Index,]
-
voice_Test <- voice_Original[-sample_Index,]
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
但是我们还没有解决之前我们发现的一些问题,数据的量纲实际上是不一样的,另外某些因子间存在高度的相关性,这对我们的建模是不利的,因此我们需要进行一些预处理,我们又需要用到preProcess 函数:
-
### preprocess factors
for further modeling
-
pp <- preProcess(voice_Train,
method=c("scale","center","pca"))
-
voice_Train <-
predict
(pp,voice_Train)
-
voice_Test <-
predict
(pp,voice_Test)
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
我们首先将数值型因子进行了标准化,确保所有的因子在一个量纲上,接着对已经标准化的数据进行主成分分析,消除因子中的高相关性。如果我们看一下我们的现在经过处理的数据,就可以看到:
-
voice
_Train
-
-
12 Variables 2218 Observations
-
-----------------------------------------------------------
-
sp
.ent
-
n missing unique
-
2218 0 2
-
-
High (1144, 52%), Low (1074, 48%)
-
-----------------------------------------------------------
-
label
-
n missing unique
-
2218 0 2
-
-
female (1109, 50%), male (1109, 50%)
-
-----------------------------------------------------------
-
PC1
-
n missing unique Info Mean
-
2218 0 2216 1 2.084e-17
-
.05 .10 .25 .50 .75
-
-5.2623 -3.8212 -2.0470 0.3775 2.0260
-
.90 .95
-
3.6648 4.5992
-
-
lowest :
-9
.885
-9
.138
-8
.560
-8
.476
-8
.412
-
highest: 6.377 6.381 6.391 6.755 6.934
-
-----------------------------------------------------------
-
PC2
-
n missing unique Info Mean
-
2218 0 2216 1 -4.945e-16
-
.05 .10 .25 .50 .75
-
-2.7216 -2.0700 -0.8694 0.2569 0.9934
-
.90 .95
-
1.5576 2.0555
-
-
lowest :
-5
.528
-5
.315
-5
.132
-5
.103
-5
.019
-
highest: 4.493 4.509 4.598 4.732 4.931
-
-----------------------------------------------------------
-
PC3
-
n missing unique Info Mean
-
2218 0 2216 1 1.579e-16
-
.05 .10 .25 .50 .75
-
-1.6818 -1.3640 -0.7880 -0.2214 0.5731
-
.90 .95
-
1.1723 1.6309
-
-
lowest :
-2
.809
-2
.536
-2
.462
-2
.443
-2
.407
-
highest: 8.055 8.299 8.410 8.805 9.229
-
-----------------------------------------------------------
-
PC4
-
n missing unique Info Mean
-
2218 0 2216 1 -3.583e-16
-
.05 .10 .25 .50 .75
-
-1.98986 -1.60536 -0.75468 0.09347 0.86320
-
.90 .95
-
1.49494 1.83657
-
-
lowest :
-7
.887
-6
.616
-5
.735
-5
.568
-4
.596
-
highest: 2.888 2.921 3.046 3.123 3.311
-
-----------------------------------------------------------
-
PC5
-
n missing unique Info Mean
-
2218 0 2216 1 -1.127e-16
-
.05 .10 .25 .50 .75
-
-1.8479 -1.2788 -0.5783 0.0941 0.6290
-
.90 .95
-
1.1909 1.5739
-
-
lowest :
-4
.595
-3
.900
-3
.887
-3
.787
-3
.760
-
highest: 3.160 3.313 3.548 3.722 3.822
-
-----------------------------------------------------------
-
PC6
-
n missing unique Info Mean
-
2218 0 2216 1 6.421e-18
-
.05 .10 .25 .50 .75
-
-1.56253 -1.03095 -0.39648 0.03999 0.53475
-
.90 .95
-
1.10113 1.38224
-
-
lowest :
-6
.971
-6
.530
-5
.521
-5
.510
-5
.320
-
highest: 1.943 1.948 2.005 2.053 2.066
-
-----------------------------------------------------------
-
PC7
-
n missing unique Info Mean
-
2218 0 2216 1 -2.789e-16
-
.05 .10 .25 .50 .75
-
-1.0995 -0.8375 -0.4970 -0.1234 0.4493
-
.90 .95
-
1.1055 1.4462
-
-
lowest :
-3
.370
-3
.132
-2
.977
-2
.813
-2
.664
-
highest: 2.951 3.136 3.863 3.937 4.128
-
-----------------------------------------------------------
-
PC8
-
n missing unique Info Mean
-
2218 0 2216 1 -7.291e-17
-
.05 .10 .25 .50 .75
-
-1.18707 -0.96343 -0.51065 -0.02345 0.46939
-
.90 .95
-
0.96676 1.28817
-
-
lowest :
-2
.644
-2
.611
-2
.477
-2
.328
-2
.261
-
highest: 2.926 2.940 2.967 2.971 3.456
-
-----------------------------------------------------------
-
PC9
-
n missing unique Info Mean
-
2218 0 2216 1 4.008e-16
-
.05 .10 .25 .50 .75
-
-1.06437 -0.84861 -0.47079 -0.04825 0.42092
-
.90 .95
-
0.96161 1.25187
-
-
lowest :
-2
.267
-2
.263
-2
.095
-2
.066
-1
.898
-
highest: 2.217 2.244 2.266 2.414 2.460
-
-----------------------------------------------------------
-
PC10
-
n missing unique Info Mean
-
2218 0 2216 1 2.387e-16
-
.05 .10 .25 .50 .75
-
-0.93065 -0.71784 -0.40541 -0.07025 0.37068
-
.90 .95
-
0.82534 1.12412
-
-
lowest :
-2
.160
-1
.810
-1
.754
-1
.744
-1
.661
-
highest: 2.164 2.292 2.349 2.385 2.654
-
-----------------------------------------------------------
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
原来的所有数值型因子已经被PC1-PC10取代了。
现在,我们进行一些通用的设置,为不同的模型进行交叉验证比较做好准备。
-
### define formula
-
model_Formula <- label~PC1+PC2+PC3+PC4+PC5+PC6+PC7+PC8+PC9+PC10+sp.ent
-
-
-
###
set
cross-validation parameters
-
-
modelControl <- trainControl(
method="repeatedcv",number=5,
-
repeats=
5,
allowParallel=
TRUE)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
下面我们开始建立我们的第一个模型:逻辑回归模型:
-
### model
1: logistic regression
-
glm_Model
<- train(model_Formula,
-
data=
voice_Train,
-
method="glm",
-
trControl
=
modelControl
)
- 1
- 2
- 3
- 4
- 5
- 1
- 2
- 3
- 4
- 5