窗函数(window function)在信号处理当中的应用(一)
窗函数在信号处理中的应用
好久没写博客了。。。哈哈。
我喜欢DSP基础研究,上次好不容易在DSP中用到了一次窗函数感觉好棒,分享给大家希望能够对大家有一些些帮助吧。
1,从两个重要极限到时域低通滤波器
两个重要极限
数学里面常常会把两个非常重要而且非常常见的极限放在一起并称他们为两个重要极限。
第一个重要极限:函数sinx/x在x趋近于0处的极限。
第二个重要极限:(1 + 1/x)^x 在x趋近于无穷大时的极限。
频域理想低通滤波器
两个重要极限的重要性从表面上看在初等函数的求导上,尤其是三角函数的求导上起到了至关重要的作用。但其博大精深的数学思想,尤其是自然数e的作用,绝对是登峰造极,无以伦比。从另一个角度看,就连高数同济六版这种SHI一样的教材都不好意思忽视这两个重要极限的重要性,其重要性就可想而知了。
言归正传,这两个重要极限中提到的sinx/x,又叫SINC FUNCTION。在数字信号处理领域里,可以说是闻名遐迩,无所不知。下图是一个理想低通滤波器,通带部分完全平坦,阻带衰减为无限大,而过渡带无限小。
Matlab代码:
%% An application of 2D window function on image processing.
% Date: early summer 2017
% Author: Z.Zhu, [email protected]
% Copy Rights Reserved.
% May not be copied, scanned, or duplicated, in whole or in part.
clear all;
close all;
%% Part I
%% Window function for DSP.
% Ideal lowpss
DataLength = 500; % Length of signal
Vector = linspace(0,0.5,DataLength); % Time vector
StepFun = ones(1,DataLength);
StepFun(DataLength/2:end) = 0;
plot(Vector,StepFun,'k','LineWidth',3);
title('Ideal lowpass filter in Freq-domain');
legend('The step function');
axis([0 0.5 -0.1 1.1]);
grid on
Sinc函数作为空间域理想低通滤波器
现在我们对这个频域理想低通滤波器做傅里叶逆变换(注意:这里是逆变换,因为是从频域到时域。),就会得到一个形如下图的空间域理想低通滤波器。
注意:上图既不是实部图也不是虚部图,而是幅值图,且经过了FFTSHIFT。
这就是著名的Sinc函数!
现在问题来了,Sinc函数是从正无穷到负无穷都存在的连续函数(如图中所示的向两边无限延伸的涟漪(ripple))。
Matlab代码:
% Sinc
spectrum = fft(StepFun);
SPECTRUM = abs(spectrum)/(DataLength/2); % sqrt(RE^2 + IM^2) and normalized
figure;
plot(fftshift(SPECTRUM),'k','LineWidth',3);
title('Ideal lowpass filter in Time-domain');
legend('The sinc function');
axis([200 300 0 1.1]);
grid on尽管这个无限长的函数在数学上没有任何问题,但是想通过计算机来实现就无能为力了。那么办呢?现在我们进入下一个话题。
2,截断和能谱的泄漏
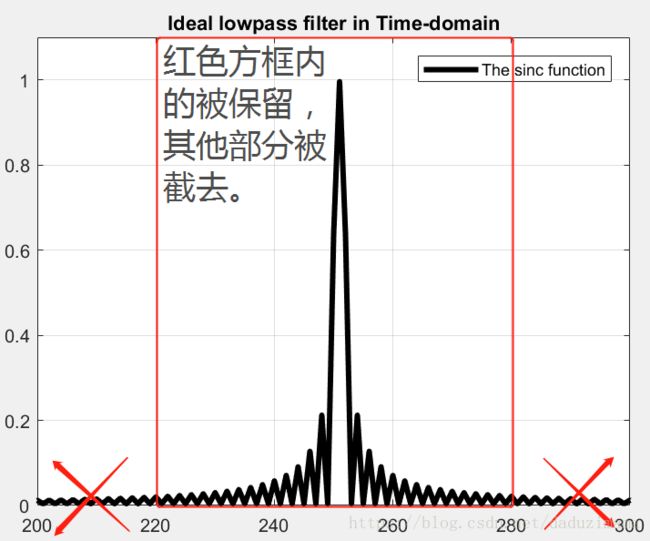
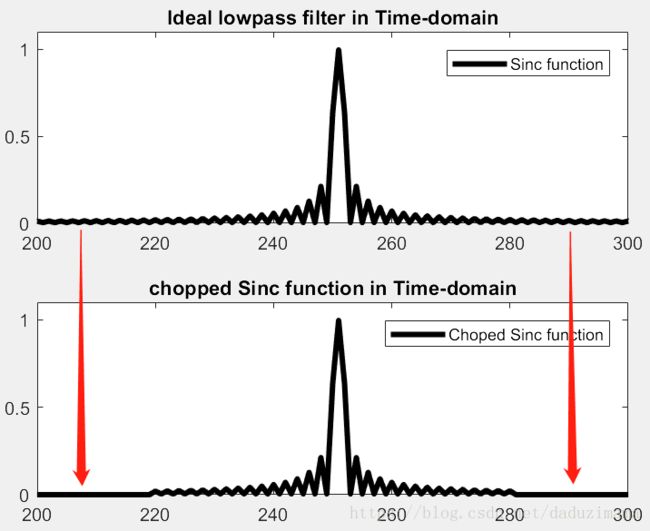
由于Sinc函数是无限的,为了便于用电脑来表示我们就只能选择其中的一段存到电脑里。如下图中,我用红框选择了整个Sinc函数其中的一段,而其他的部分全部都被砍掉了,这样的突然砍断,带来了信号的不连续,即,信号的跳变。这种不连续直接导致了频谱的泄漏。频谱发生了畸变,原来非常集中的能量被分散到较宽的频带中去了。
下图是截断前后的比较
Matlab代码:
% Chopoff
CutSize = 30;
Chopoff = zeros(1,size(SPECTRUM,2));
temp = fftshift(spectrum);
Chopoff(DataLength/2 - CutSize : DataLength/2 + CutSize) = temp(DataLength/2 - CutSize : DataLength/2 + CutSize);
ChopedSinc = abs(Chopoff)/(DataLength/2); % normalize
figure;
subplot(2,1,1)
plot(fftshift(SPECTRUM),'k','LineWidth',3);
title('Ideal lowpass filter in Time-domain');
legend('Sinc function');
axis([200 300 0 1.1]);
grid on
subplot(2,1,2)
plot(ChopedSinc,'k','LineWidth',3);
title('chopped Sinc function in Time-domain');
legend('Choped Sinc function');
axis([200 300 0 1.1]);
grid on
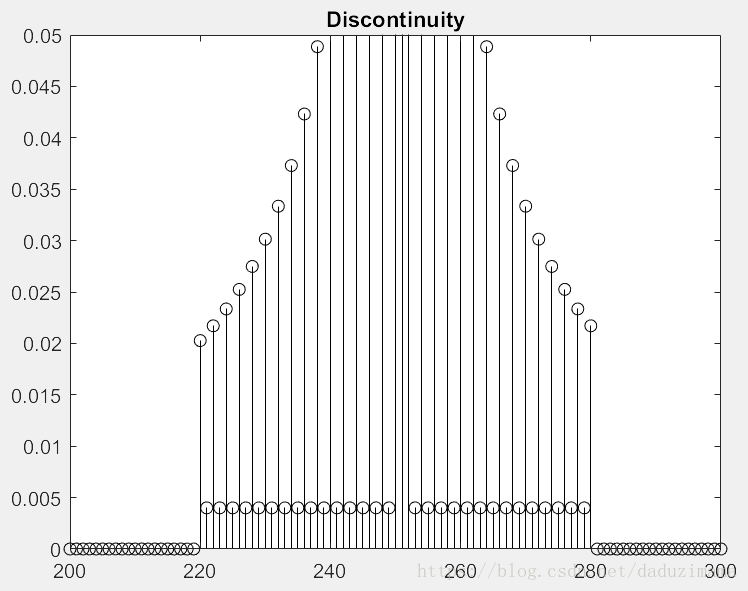
信号的突然截断导致了信号的不连续,为了显示这种数字化信号的不连续,这里我选择了另外一种绘图方式来绘制。为了显示方便,原图中高于0.05的部分被削去,为了突出截断处的不连续。
Matlab代码:
% Stem for its Discontinuity
figure;
stem(ChopedSinc,'k');
title('Discontinuity');
axis([200 300 0 .05]);
grid on这样的突然间断会对该信号的频谱带来难以预估的影响,也就是我们常说的能谱的泄漏!
下次再为大家娓娓道来。
(全文完)
谢谢收看!
鸣谢:
【1】Matlab 2017a
【2】托马斯微积分
【3】[Steven W. Smith] The Scientist and Engineer's Guide to Digital Signal Processing(1999)
《圣经》 马太福音19章19节 ------ 当孝敬父母,又当爱人如己。
*配图和本文无关*