窗函数（window function）在信号处理当中的应用（二）

 

窗函数在信号处理中的应用

 

      上次我们只是提到了对突然截断后的不连续信号进行傅里叶变换后，它的新频谱就会发生一系列的变化（泄漏），现逐一说明：

 

1，振荡

如果把截断后的信号进行傅里叶逆变换重新变回到频域，其结果并不是原来那种理想滤波器而会出现剧烈的抖动/振荡。

 

Matlab代码：

% Ripple
CHOPOFF = abs((ifft(Chopoff)));
figure;
plot(CHOPOFF,'k','linewidth',2);
title('Choped off lowpass filter in Freq-domain');
legend('Ripple');

 

2，幅值的衰减

 

     这里我需要借用正弦函数来说明。下图是一个标准的正弦函数及其傅里叶变换后的频谱图，由于正弦函数也是沿着X轴两边无限延伸的连续函数。

 

为了用电脑来表示和保存它，所以要对它进行有选择的截断，如下图所示。

 

下图为截断后的新信号及其傅里叶频谱

 

下图为原始信号的频谱和截断后信号的频谱的比较

 

3，拖尾

 

原本非常规则，集中的频谱，因为时域信号的突然截断和不连续，出现了不希望看到的频谱的拓宽和畸变。

 

     综上：信号能谱的泄露会往往会出现上述三种情况，抖动，拖尾和幅值的衰减，究其根本原因主要是因为，信号的突然截断，产生了一个新的跳变的，不连续的，非周期的信号。

 

 

Matlab代码：

% choped sinewave
Fs = 1000;            % Sampling frequency
T = 1/Fs;             % Sampling period
L = 1000;             % Length of signal
t = (0:L-1)*T;        % Time vector
% Form a signal containing a 120 Hz sinusoid of amplitude 1.
S = sin(2.*pi.*50.*t);
figure;
plot(S)

% chop off a part of signal from original one
s = S(10:120);
figure;
plot(s)

% replicate chopped signal
sReplicate = repmat(s,1,5);
figure;
plot(sReplicate)

% spectrum of original signal
YS = fft(S);
yS = abs(YS/L);         % normalization
figure;
plot(fftshift(yS))

% spectrum of chopped signal
Ys = fft(s);
ys = abs(Ys/size(Ys,2)); % normalization
figure;
plot(fftshift(ys))

 

                               窗函数在SINC FUNCTION反变换中的应用

现在我们回到之前的带有剧烈振荡的频域理想低通滤波器，如下图所示，还记得吗？

 

      为了避免突然截断带来的振荡，信号处理的工程师们常常会选择在进行傅里叶反变换之前对截断后的信号进行加窗处理。窗的种类有很多，大多数是在上世纪50年代为其命名的，其中有两个比较常用的，一个是汉明窗（Hamming），一个是布莱克曼窗(Blackman)。这两个窗函数的滤波器参数详细比较如下，鉴于我这次主要不是专讲DSP，这里就不详细拓展了（当然了，我自己在这方面也不是完全了解），这是给出了教科书中的一个经典截图，如下。而我们这次的实验就要使用布莱克曼窗！

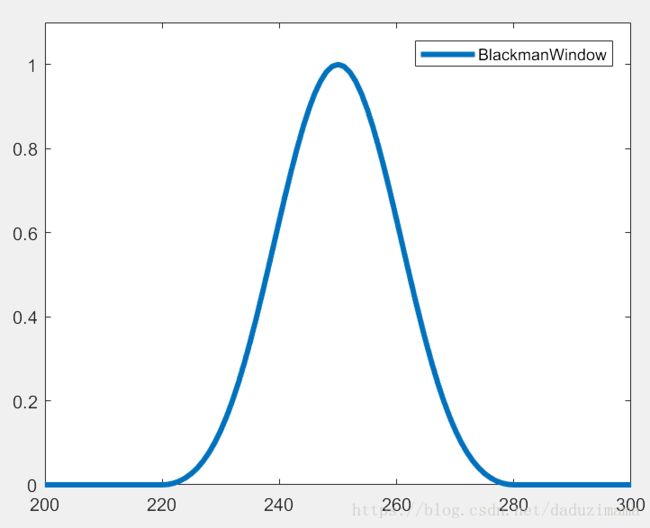
     下图为我在MATLAB中生成的Blackman窗函数。注意：窗函数的长度即SIZE一定要和原始信号的长度相同。但是为了显示和突出我想说明的重点，我在写这篇文章的时候，很多地方的长度都不是一致的，请读者注意。

 

Matlab代码：

% form window function
BlackmanWindow = zeros(1,size(CHOPOFF,2));
BlackmanWindow(DataLength/2 - CutSize : DataLength/2 + CutSize) = blackman(2*CutSize + 1)';
figure;
plot(BlackmanWindow,'linewidth',3);
legend('BlackmanWindow');
axis([200 300 0 1.1]);

 

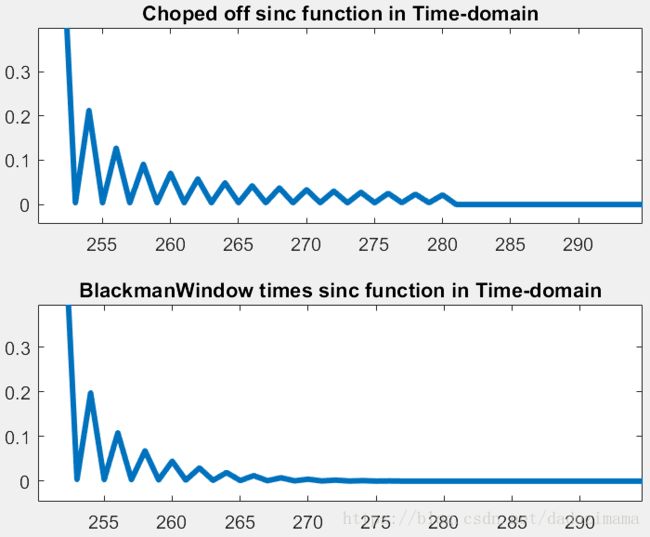
接下来用布莱克曼窗乘以被加窗的信号，效果如下图所示。

 

 

细节放大比较，注意不连续的跳变被极大的平滑掉了。

 

Matlab代码：

% windowed(magnitude only)
SincWindowed = ChopedSinc .* BlackmanWindow;
figure;
subplot(2,1,1)
plot(abs((ChopedSinc)),'linewidth',3);
title('Choped off sinc function in Time-domain');
axis([200 300 0 inf]);
subplot(2,1,2)
plot(abs((SincWindowed)),'linewidth',3);
title('BlackmanWindow times sinc function in Time-domain');
axis([200 300 0 inf]);

 

现在对加窗后的新信号进行傅里叶逆变换，看看新的频域低通滤波器会是什么样。

 

 

Matlab代码：

% Fourier tranform of windowed function 
SINCWINDOW = Chopoff .* BlackmanWindow;
SINCWINDOW = (abs(ifft((SINCWINDOW))));
figure;
subplot(1,2,1)
plot(CHOPOFF,'k','linewidth',2);
title('Choped off lowpass filter in Freq-domain');
legend('Ripple');
axis([0 505 0 1.2]);
subplot(1,2,2)
plot(SINCWINDOW,'k','linewidth',2);
title('windowed Sinc freqency response');
legend('Smooth roll-off/ Ripple eliminated');
axis([0 505 0 1.2]);

 

                                               总结 ——— 流程图

谢谢大家花时间阅读，这一部分我主要是讲的窗函数在DIP中的使用，下次我分享一下窗函数在图像中的应用实战。

（全文完）

 

鸣谢：

【1】Matlab 2017a

【2】[Steven W. Smith] The Scientist and Engineer's Guide to Digital Signal Processing (1999)

 

谢谢收看！

再见！

 

《圣经》 彼得前书5章5节  -------  神阻挡骄傲的人，赐恩给谦卑的人。

                                                                                              *配图和本文无关*