棋盘覆盖问题(分治,递归)
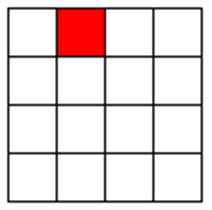
在一个2^k * 2^k个方格组成的棋盘中,恰有一个方格与其他方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。
该棋盘为特殊棋盘,红色的方格为特殊方格。
棋盘覆盖问题是指,要用图2中的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。 图二
图二
该问题就是在考察分治的思想,将大棋盘分为一个个的小棋盘,直到分为1*1的小棋盘。具体算法如下。
当k>0时,将2k×2k棋盘分割为4个2k-1×2k-1 子棋盘(a)所示。
特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,如 (b)所示,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为棋盘1×1。
#include
#include
int count=1;
void Qipanfugai(int x,int y,int a,int b,int t)
{
if(t==1)
return;
int r=t/2;
if(a,<%d,%d>,<%d,%d>\n\n",count++,x+r-1,y+r,x+r,y+r,x+r,y+r-1);
Qipanfugai(x,y,a,b,r);
Qipanfugai(x,y+r,x+r-1,y+r,r);
Qipanfugai(x+r,y,x+r,y+r-1,r);
Qipanfugai(x+r,y+r,x+r,y+r,r);
}
if(a>=x+r&&b,<%d,%d>,<%d,%d>\n\n",count++,x+r-1,y+r-1,x+r,y+r,x+r,y+r-1);
Qipanfugai(x,y,y+r-1,x+r-1,r);
Qipanfugai(x,y+r,a,b,r);
Qipanfugai(x+r,y,x+r,y+r-1,r);
Qipanfugai(x+r,y+r,x+r,y+r,r);
}
if(a=y+r)
{
printf("第%5d步 放在<%d,%d>,<%d,%d>,<%d,%d>\n\n",count++,x+r-1,y+r,x+r,y+r,x+r-1,y+r-1);
Qipanfugai(x,y,y+r-1,x+r-1,r);
Qipanfugai(x,y+r,x+r-1,y+r,r);
Qipanfugai(x+r,y,a,b,r);
Qipanfugai(x+r,y+r,x+r,y+r,r);
}
if(a>=x+r&&y>=y+r)
{
printf("第%5d步 放在<%d,%d>,<%d,%d>,<%d,%d>\n\n",count++,x+r-1,y+r,x+r,y+r-1,x+r-1,y+r-1);
Qipanfugai(x,y,y+r-1,x+r-1,r);
Qipanfugai(x,y+r,x+r-1,y+r,r);
Qipanfugai(x+r,y,x+r,y+r-1,r);
Qipanfugai(x+r,y+r,a,b,r);
}
}
int main()
{
Qipanfugai(1,1,1,1,32); //这里假设的是32*32的棋盘,且特殊方块位于(1,1)
return 0;
}