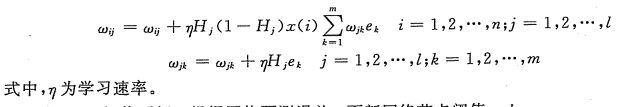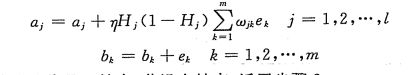BP神经网络原理

结构

单个神经元

多个神经元

Xn是输入，Ym是输出，Wij是输入层结点i到中间层结点j的权值，Wjk是中间层结点j到输出层结点K的权值。

训练算法

网络初始化

隐含层输出

输出 = 权值 X 输入— 阈值
隐含层结点j的输出 Hj = （各个输入结点 X 各权值 — 中间层阈值）的和


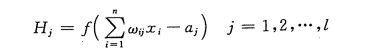
用该函数作为隐含层激励函数的原因

输出层计算

误差计算

误差 = 期望输出 — 上面的Ok

权值更新

阈值更新

最速下降法

为什么相邻两次搜索方向垂直

参数更新的依据

代码实现

# -*- coding: utf-8 -*-

import random
import numpy as np

class Network(object):

    def __init__(self, sizes):
    """参数sizes表示每一层神经元的个数，如[2,3,1],表示第一层有2个神经元，第二层有3个神经元，第三层有1个神经元."""
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(sizes[:-1], sizes[1:])]

    def feedforward(self, a):
        """前向传播"""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            test_data=None):
        """随机梯度下降"""
        if test_data: 
            n_test = len(test_data)
        n = len(training_data)
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta)
            if test_data:
                print "Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), n_test)
            else:
                print "Epoch {0} complete".format(j)

    def update_mini_batch(self, mini_batch, eta):
        """使用后向传播算法进行参数更新.mini_batch是一个元组(x, y)的列表、eta是学习速率"""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]

    def backprop(self, x, y):
        """返回一个元组(nabla_b, nabla_w)代表目标函数的梯度."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # 前向传播
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        """l = 1 表示最后一层神经元，l = 2 是倒数第二层神经元, 依此类推."""
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

    def evaluate(self, test_data):
        """返回分类正确的个数"""
        test_results = [(np.argmax(self.feedforward(x)), y) for (x, y) in test_data]
        return sum(int(x == y) for (x, y) in test_results)

    def cost_derivative(self, output_activations, y):
        return (output_activations-y)

def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    """sigmoid函数的导数"""
    return sigmoid(z)*(1-sigmoid(z))
--------------------- 
作者：雪伦_ 
来源：CSDN 
原文：https://blog.csdn.net/a819825294/article/details/53393837 
版权声明：本文为博主原创文章，转载请附上博文链接！