Opencv决策树分类器应用
机器学习在数据挖掘、计算机视觉、搜索引擎、医学诊断、证券市场分析、语言与手写识别等领域有着十分广泛的应用,特别是在数据分析挥着越来越重要的作用。在机器学习中,决策树是最基础且应用最广泛的归纳推理算法之一,基于决策树算法,衍生出很多出色的集成算法,如random forest、adaboost、gradient tree boostiong等。
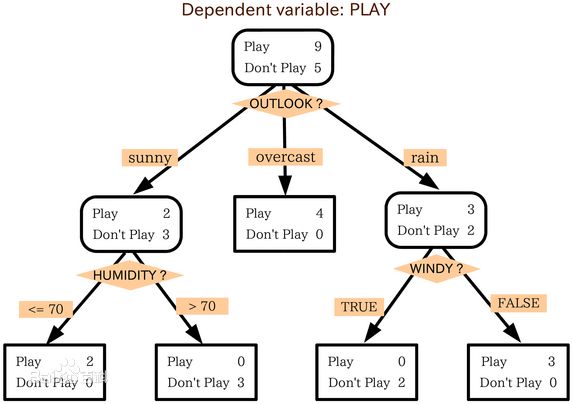
决策树构建的基本步骤如下:
1.开始,所有记录看作一个节点
2.遍历每个变量的每一种分割方式,找到最好的分割点
3.分割成两个节点N1和N2
4.对N1和N2分别继续执行2-3步,直到每个节点足够“纯”为止
决策树归纳是从有类标号的训练元中学习决策模型。常用的决策树算法有ID3,C4.5和CART。它们都是采用贪心(即非回溯的)方法,自顶向下递归的分治方法构造。这几个算法选择属性划分的方法各不相同,ID3使用的是信息增益,C4.5使用的是信息增益率,而CART使用的是Gini基尼指数。
何为信息熵?信息熵是跟所有可能性有关系的。每个可能事件的发生都有个概率。信息熵就是平均而言发生一个事件我们信息量大小。所以数学 上,信息熵其实是信息量的期望。熵越大,说明系统越混乱,携带的信息就越少。熵越小,说明系统越有序,携带的信息就越多。
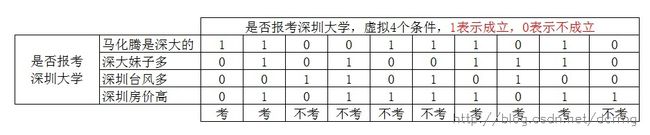
以下是根据4个条件的成立与否,来决定是否报考深圳大学,通过这10个样本生成决策树,进而对输入的4个条件来判断是否报考深大,以下是样本数据:
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/ml/ml.hpp"
#include
using namespace cv;
using namespace std;
int main( int argc, char** argv )
{
//10个训练样本
float trainingDat[10][4]={{1,0,0,0},{1,1,0,1},{0,0,1,0},
{0,1,1,1},{1,0,0,0},{1,0,1,1},{1,1,1,1},{0,1,1,0},{1,1,0,1},{0,0,0,1}};
Mat trainingDataMat(10,4,CV_32FC1,trainingDat);
//样本的分类结果,作为标签供训练决策树分类器
float responses[10]={1,1,0,0,0,0,1,1,1,0}; // 1代表考取,0代表不考
Mat responsesMat(10,1,CV_32FC1,responses);
float priors[4]={1,1,1,1}; //先验概率,这里每个特征的概率都是一样的
//定义决策树参数
CvDTreeParams params(15, //决策树的最大深度
1, //决策树叶子节点的最小样本数
0, //回归精度,本例中忽略
false, //不使用替代分叉属性
25, //最大的类数量
0, //不需要交叉验证
false, //不需要使用1SE规则
false, //不对分支进行修剪
priors //先验概率
);
//掩码
Mat varTypeMat(5,1,CV_8U,Scalar::all(1));
CvDTree tree;
tree.train(trainingDataMat, //训练样本
CV_ROW_SAMPLE, //样本矩阵的行表示样本,列表示特征
responsesMat, //样本的响应值矩阵
Mat(),
Mat(),
varTypeMat, //类形式的掩码
Mat(), //没有属性确实
params //决策树参数
);
CvMat varImportance;
varImportance=tree.getVarImportance();
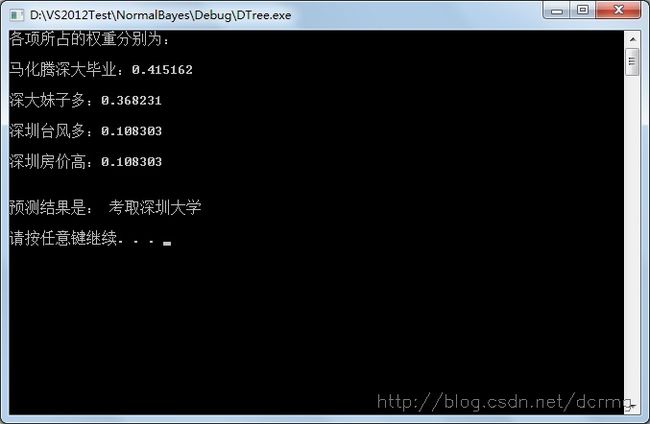
cout<<"各项所占的权重分别为:\n\n";
string item;
for(int i=0;ivalue; //获得预测结果
if(r==(double)1.0)
{
cout<