C++实现遥感图像PCA融合

前段时间由于项目需要，用C++实现了基于PCA的图像融合算法。一开始低估了这个算法在遥感图像上的实现难度，对算法的详细流程没有完全的了解清楚，因为PCA的实现是非常简单的，仅仅需要计算特征值和特征矩阵就能够实现图像的PCA变换。而实现遥感图像的PCA融合，还有一个步骤非常重要，就是遥感图像的直方图匹配问题。网上绝大多数图像直方图匹配的算法都是基于256阶灰度值的，最后计算出来的图像变换映射是整型数据，因此可以直接放在变换数组中作为下标使用，达到映射的效果（这里太细节的东西看不懂没关系，我后面会详细阐述）。而遥感图像往往并不是8位图像，也就不是256个灰度级，其中还有很大一部分图像是浮点型的数据，因此并不能完全依照网上的很多方法实现。需要一些变换处理，而这也是当时困扰我的一个因素。还好后来简单变换一下实现了，虽然变换比较简单，但是我也分享出来，希望能够对读者有所帮助。

PS:我永远都调不好CSDN博客文章的排版。。。怎么这么难用的排版工具。

为了连贯起见，下面我将会把整个算法的流程都详细阐述一遍，并附上我的相应代码。对算法流程已经比较了解的读者，可以直接往下看完整的代码。需要说明的是：代码只用到GDAL库，因此不用担心别的依赖库的问题。

PCA(Principal Component Analysis,主成分分析)，简单点说就是利用计算出来的较少的主成分变量，来代替原始数据所有维度，以达到数据降维的目的。关于PCA的文章和原理的介绍网上非常多，这里我就不做详细的描述了，推荐一个李民录博客里的PCA吧：http://blog.csdn.net/liminlu0314/article/details/8957009

图像融合，就是将低空间分辨率的影像和高空间分辨率的单波段全色影像进行融合，以充分利用不同数据的信息。经过融合后的影像，既具有了高空间分辨率，又较好的保留了原始的多个波段的信息。PCA融合只是众多融合算法当中的一种，可能也是原理最直观、简单的一种。理解了PCA，对于理解PCA融合就非常容易了。将原始遥感影像进行PCA变换后，得到的第一主成分，是包含信息量最大的主成分，图像呈现灰度全色图像样子。于是产生了PCA融合的直观想法：如果利用灰度值信息更丰富，空间分辨率更高的遥感全色影像来替换原始影像经PCA变换后得到的第一主成分，再进行PCA反变换，是不是就能够丰富原始遥感影像的空间分辨率信息呢？事实上，基于PCA的图像融合技术，正是这么一个直观的思路。所以算法的流程非常简单：

原始图像--->重采样到全色图像大小---> PCA变换得到主成分图像------>用全色图像“替换”第一主成分----->PCA反变换

这里的“替换”被打上双引号并加粗是有意而为的，因为这里的替换并不是简单的将图像波段换一下就能行的（事实上我一开始在没有完全了解算法流程的时候就只是简单换掉第一主成分，后来得到的结果总是不对）。一幅图像要能够替代另外一幅图像，它们之间包含的信息应该尽可能的相似，而体现图像信息的正是图像的灰度值分布，也就是图像的直方图，若两幅图像的直方图大致一样，则这两幅图像中灰度值分布也就大致一样，才能够进行“替换”。了解到这里，就能知道PCA融合的关键除了PCA算法，还有就是图像的直方图匹配。（如果有不了解直方图以及直方图匹配原理的同学，在网上搜一下，有很多。）

下面我们开始进入算法的流程，我会边将原理，边附上我的代码帮助大家理解。

1、首先，是GDAL读取遥感影像并判断数据类型，以及代融合的两幅影像是否大小相等，我想这个我就不再啰嗦了吧，直接给大家附上代码吧。（说明：由于是特殊要求，需要4个波段的影像，我才把波段数也作为判断的一个条件，而读者使用时下面的波段数完全可以更改）

 

    GDALAllRegister();
    CPLSetConfigOption( "GDAL_FILENAME_IS_UTF8", "NO" );
    
    // 打开多波段图像
    multiDataset = ( GDALDataset* )GDALOpen( multiFilename.c_str(), GA_ReadOnly );
    if( multiDataset == NULL )
    {
        cout << "打开多波段图像失败！" << endl;
        throw multiFilename + "file not valid";
        return;
    }
    int multiWidth = multiDataset->GetRasterXSize();
    int multiHeight = multiDataset->GetRasterYSize();
    int multiBandCount = multiDataset->GetRasterCount();
    
    
    // 验证是否为4波段数据
    if ( multiBandCount != 4 )
    {
        cout << "图像波段数有误，目前只能处理4波段图像！" << endl;
        throw multiFilename + "file not valid";
        return;
    }
    
    // 打开高分辨率图像
    highResDataset = ( GDALDataset* )GDALOpen( highRSFilename.c_str(), GA_ReadOnly );
    if( highResDataset == NULL )
    {
        cout << "打开高分辨率图像失败！" << endl;
        throw highRSFilename + "file not valid";
        return;
    }
    int highResWidth = highResDataset->GetRasterXSize();
    int highResHeight = highResDataset->GetRasterYSize();
    
    // 判断两幅图像是否等大小
    if ( highResHeight != multiHeight || highResWidth != multiWidth )
    {
        cout << "图像大小不一致" << endl;
        throw multiFilename + "and" + highRSFilename + "don't match...";
        return;
    }

 

 

2、PCA变换

a.计算原始影像的协方差矩阵

 

    double* bandMean = calMean( multiDataset );// 计算波段均值
    double* covMatrix = calCovMatrix( multiDataset, bandMean );// 计算协方差矩阵

/// 

/// 计算图像波段均值.
/// 
/// 图像数据集.
/// double * 图像均值向量.
double* PcaFusion::calMean( GDALDataset * dataset )
{
    double* bandMean = new double [this->bandCount];
    for ( int i = 0; i < this->bandCount; i++ )
    {
        double dMaxValue, dMinValue;
        multiDataset->GetRasterBand( i + 1 )->ComputeStatistics( FALSE, &dMinValue, &dMaxValue, bandMean + i, 0, NULL, NULL );
    }
    if ( bandMean == NULL )
    {
        cout << "统计波段均值失败！" << endl;
        return NULL;
    }
    return bandMean;
}

/// 

/// 计算协方差矩阵.
/// 
/// 图像数据集.
/// 图像波段均值向量.
/// double * 图像协方差矩阵.
double* PcaFusion::calCovMatrix( GDALDataset * dataset, double * bandMean )
{
    double *dCovariance = new double[this->bandCount * this->bandCount];
    int index = 0;
    for ( int i = 0; i < this->bandCount; i++ )
    {
        float* poData1 = new float[ this->height * this->width];
        int bandList = {i + 1};
        multiDataset->RasterIO( GF_Read, 0, 0, this->width, this->height, poData1, this->width, this->height, GDT_Float32, 1, &bandList, 0, 0, 0 );
        
        for ( int j = 0; j < this->bandCount; j++ )
        {
            float* poData2 = new float[ this->height * this->width];
            int bandList = {j + 1};
            multiDataset->RasterIO( GF_Read, 0, 0, this->width, this->height, poData2, this->width, this->height, GDT_Float32,  1, &bandList, 0, 0, 0  );
            double sum = 0;
            
            for ( int pix = 0; pix < this->height * this->width; pix++ )
            {
                sum += ( poData1[pix] - bandMean[i] ) * ( poData2[pix] - bandMean[j] );
            }
            dCovariance[index++] = sum * 1.0 / (  this->height * this->width - 1 );
        }
    }
    return dCovariance;
}

 

b.计算协方差矩阵的特征值、特征向量。这里采用雅格比(Jacobi)方法求实对称矩阵的全部特征值及特征向量。（计算函数为李民录提供）

 

// 计算协方差所形成的矩阵的特征值与特征向量
    double eps = 0.0001;   //控制精度要求
    double *eigenVector = new double[this->bandCount * this->bandCount];
    eejcb( covMatrix, this->bandCount, eigenVector, eps, 100000 );

 

/// 

/// 利用雅格比(Jacobi)方法求实对称矩阵的全部特征值及特征向量.
/// 
/// 长度为n*n的数组，存放实对称矩阵，返回时对角线存放n个特征值.
/// 矩阵的阶数.
/// 长度为n*n的数组，返回特征向量(按列存储).
/// 控制精度要求.
/// 整型变量，控制最大迭代次数.
/// 返回false表示超过迭代jt次仍未达到精度要求，返回true表示正常返回.
bool PcaFusion::eejcb( double a[], int n, double v[], double eps, int jt )
{
    int i, j, p, q, u, w, t, s, l;
    double fm, cn, sn, omega, x, y, d;
    
    l = 1;
    //初始化特征向量矩阵使其全为0
    for( i = 0; i <= n - 1; i++ )
    {
        v[i * n + i] = 1.0;
        for( j = 0; j <= n - 1; j++ )
        {
            if( i != j )
                v[i * n + j] = 0.0;
        }
    }
    
    while( true ) //循环
    {
        fm = 0.0;
        for( i = 0; i <= n - 1; i++ )   // 出, 矩阵a( 特征值 ), 中除对角线外其他元素的最大绝对值
        {
            //这个最大值是位于a[p][q] ,等于fm
            for( j = 0; j <= n - 1; j++ )
            {
                d = fabs( a[i * n + j] );
                
                if( ( i != j ) && ( d > fm ) )
                {
                    fm = d;
                    p = i;
                    q = j;
                }
            }
        }
        
        if( fm < eps )   //精度复合要求
            return true; //正常返回
            
        if( l > jt )     //迭代次数太多
            return false;//失败返回
            
        l ++;       //   迭代计数器
        u = p * n + q;
        w = p * n + p;
        t = q * n + p;
        s = q * n + q;
        x = -a[u];
        y = ( a[s] - a[w] ) / 2.0;		//x y的求法不同
        omega = x / sqrt( x * x + y * y );	//sin2θ
        
        //tan2θ=x/y = -2.0*a[u]/(a[s]-a[w])
        if( y < 0.0 )
            omega = -omega;
            
        sn = 1.0 + sqrt( 1.0 - omega * omega );
        sn = omega / sqrt( 2.0 * sn );		//sinθ
        cn = sqrt( 1.0 - sn * sn );			//cosθ
        
        fm = a[w];   //   变换前的a[w]   a[p][p]
        a[w] = fm * cn * cn + a[s] * sn * sn + a[u] * omega;
        a[s] = fm * sn * sn + a[s] * cn * cn - a[u] * omega;
        a[u] = 0.0;
        a[t] = 0.0;
        
        //   以下是旋转矩阵,旋转了了p行,q行,p列,q列
        //   但是四个特殊点没有旋转(这四个点在上述语句中发生了变化)
        //   其他不在这些行和列的点也没变
        //   旋转矩阵,旋转p行和q行
        for( j = 0; j <= n - 1; j++ )
        {
            if( ( j != p ) && ( j != q ) )
            {
                u = p * n + j;
                w = q * n + j;
                fm = a[u];
                a[u] = a[w] * sn + fm * cn;
                a[w] = a[w] * cn - fm * sn;
            }
        }
        
        //旋转矩阵,旋转p列和q列
        for( i = 0; i <= n - 1; i++ )
        {
            if( ( i != p ) && ( i != q ) )
            {
                u = i * n + p;
                w = i * n + q;
                fm = a[u];
                a[u] = a[w] * sn + fm * cn;
                a[w] = a[w] * cn - fm * sn;
            }
        }
        
        //记录旋转矩阵特征向量
        for( i = 0; i <= n - 1; i++ )
        {
            u = i * n + p;
            w = i * n + q;
            fm = v[u];
            v[u] = v[w] * sn + fm * cn;
            v[w] = v[w] * cn - fm * sn;
        }
    }
    
    return true;
}

 

 

c.将特征值特征向量进行排序

 

/// 

/// 按特征值大小排列特征向量.
/// 
/// 特征向量.
/// 经过Jacobi方法返回的原协方差矩阵，对角线为特征值.
void PcaFusion::sortEigenVector( double * eigenVector, double * covAfterEejcb )
{
    for( int i = 0; i < this->bandCount - 1; i++ )
    {
        for( int j = i + 1; j < this->bandCount; j++ )
        {
            if( covAfterEejcb[j * this->bandCount + j] > covAfterEejcb[i * this->bandCount + i] )
            {
                double temp = 0;
                temp = covAfterEejcb[j * this->bandCount + j];
                covAfterEejcb[j * this->bandCount + j] = covAfterEejcb[i * this->bandCount + i];
                covAfterEejcb[i * this->bandCount + i] = temp;
                for( int k = 0; k < this->bandCount; k++ )
                {
                    temp = 0;
                    temp = eigenVector[k * this->bandCount + j];
                    eigenVector[k * this->bandCount + j] = eigenVector[k * this->bandCount + i];
                    eigenVector[k * this->bandCount + i] = temp;
                }
            }
        }
    }
}

 

 

d.原始影像矩阵与特征向量矩阵相乘，得到变换后的主成分

 

/// 

/// PCA变换.
/// 
/// 图像矩阵.
float** PcaFusion::PCATransform( float **imgMatrix, double * eigenVector )
{
    double **vec = new double*[this->bandCount];
    for ( int i = 0; i < this->bandCount; i++ )
    {
        vec[i] = new double[this->bandCount];
        for ( int j = 0; j < this->bandCount; j++ )
        {
            vec[i][j] = eigenVector[i + j * this->bandCount];
        }
    }
    
    // 构造结果矩阵
    float** result = new float*[this->bandCount];
    for ( int i = 0; i < this->bandCount; i++ )
    {
        result[i] = new float[this->width * this->height];
        for ( int j = 0; j < this->width * this->height ; j++ )
        {
            result[i][j] = 0;
        }
    }
    
    // 矩阵相乘
    for ( int i = 0; i < this->bandCount; i++ )
    {
        for ( int j = 0; j < this->height * this->width; j++ )
        {
            for ( int k = 0; k < this->bandCount; k++ )
            {
                result[i][j] += vec[i][k] * imgMatrix[k][j];
            }
        }
    }
    return result;
}

 

 

3、得到全色遥感影像向量，并与PCA变换得到的第一主成分进行直方图匹配。

 

 

这里需要先统计两幅影像的直方图，再将直方图进行匹配。网上很多代码和原理都是基于256个灰度阶数来计算的，其实直方图并非都是256个级别，因此将直方图范围扩大一点就行了。不明白原理的同学一定要去学习一下背后的数据原理，不然很难理解我下面的代码。

   

// 统计img最值
    double imgMax = -100000, imgMin = 100000;
    for ( int index = 0; index < width * height; index++ )
    {
        if ( imgMax < img[index] )
        {
            imgMax = img[index];
        }
        if ( imgMin > img[index] )
        {
            imgMin = img[index];
        }
    }
    
    // 统计ref最值
    double refMax = -100000, refMin = 100000;
    for ( int index = 0; index < width * height; index++ )
    {
        if ( refMax < ref[index] )
        {
            refMax = ref[index];
        }
        if ( refMin > ref[index] )
        {
            refMin = ref[index];
        }
    }
    
    // 变换img元素值到ref元素值范围
    for ( int i = 0; i < width * height; i++ )
    {
        img[i] = ( img[i] - imgMin ) / ( imgMax - imgMin );
        img[i] = img[i] * ( refMax - refMin ) + refMin;
    }
    
    // 再次统计img最值
    imgMax = -100000, imgMin = 100000;
    for ( int index = 0; index < width * height; index++ )
    {
        if ( imgMax < img[index] )
        {
            imgMax = img[index];
        }
        if ( imgMin > img[index] )
        {
            imgMin = img[index];
        }
    }
    
    // 将img和ref复制一份，分别把复制的数组乘以factor，变成整型
    int* imgCopy = new int[width * height];
    int* refCopy = new int[width * height];
    for ( int i = 0; i < width * height; i++ )
    {
        imgCopy[i] = ( int )( img[i] * factor );
        refCopy[i] = ( int )( ref[i] * factor );
    }
    delete ref;
    
    int imgCopyMax = imgMax * factor;
    int imgCopyMin = imgMin * factor;
    int refCopyMax = refMax * factor;
    int refCopyMin = refMin * factor;
    
    // 分别统计两幅影像的直方图
    int length = imgCopyMax - imgCopyMin + 1;
    int* imgHist = new int[length];
    int* refHist = new int[length];
    // 清零
    for( int i = 0; i < length; i++ )
    {
        imgHist[i] = 0;
        refHist[i] = 0;
    }
    
    for ( int i = 0; i < width * height; i++ )
    {
        int val = imgCopy[i] - imgCopyMin;
        imgHist[val] += 1;
        
        int val2 = refCopy[i] - imgCopyMin;
        refHist[val2] += 1;
    }
    

 
  
 

注意以上代码中，我将原始浮点型的数据乘上了一个 factor ，变成了整型，这个很关键。这个 factor 的默认值我设置的 100 。

 

 

下面我们再来具体说matchHistogram()函数，要匹配直方图，需要先利用直方图得到累积分布函数(cumulative distribution function)，其实也就是统计每个直方图中值的概率分布，得到一个概率分布函数。

 

// returns the cumulative distribution function for histogram h
double* PcaFusion::cdf( int* h, int length )
{
    int n = 0;
    for( int i = 0; i < length - 1; i++ )
    {
        n += h[i];
    }
    double* p = new double[length];
    int c = h[0];
    p[0] = ( double )c / n;
    for( int i = 1; i < length - 1; i++ )
    {
        c += h[i];
        p[i] = ( double )c / n;
    }
    return p;
}

 

 

然后是利用累积分布函数计算变换映射函数。

 

// returns the mapping function to be applied to image
int* PcaFusion::matchHistogram( int* hA, int* hR, int length )
{
    double* pA = cdf( hA, length );
    double* pR = cdf( hR, length );
    int* fun = new int[length];
    
    for( int a = 0; a < length; a++ )
    {
        int j = length - 1;
        do
        {
            fun[a] = j;
            j--;
        }
        while ( j >= 0 && pA[a] <= pR[j] );
    }
    return fun;
}

 

有了映射函数，那直接将原始数据进行相应的映射就行了，记住要除以之前的那个factor，将数据变回浮点型。

 

    for ( int i = 0; i < width * height; i++ )
    {
        imgCopy[i] = fun[imgCopy[i] - imgCopyMin] + imgCopyMin;
        img[i] = imgCopy[i] / factor;
    }
  
 
 

到了这里就明白为什么要变成整型数据了，因为这里得到的映射函数，是将原始图像的值作为输入的，而在这里是下标，所以必须是整型才行。

4、用匹配后的全色影像替换第一主成分

 

// 用高分辨率图像替换第一主分量
    int bandList = {1};
    float *highData = new float[this->width * this->height];
    highResDataset->RasterIO( GF_Read, 0, 0, this->width, this->height, highData, this->width, this->height, GDT_Float32, 1, &bandList, 0, 0, 0 );
    
    projToRange( highData, resAfterPCA[0] );// 这里调用的是统计直方图，并进行直方图匹配那部分的内容
    
    resAfterPCA[0] = highData;

 

5、PCA反变换

 

/// 

/// PCA逆变换.
/// 
/// 图像矩阵.
float** PcaFusion::inversePCA( float **imgMatrix, double * eigenVector )
{
    // 求特征向量矩阵的逆矩阵
    inverseMatrix( eigenVector, this->bandCount );
    float** resAfterInversPCA = PCATransform( imgMatrix, eigenVector );
    return resAfterInversPCA;
}

 

6、输出结果

 

/// 

/// 保存图像到文件.
/// 
/// 图像格式字符串.
void PcaFusion::saveFile( float** pResult, const char* format )
{
    // 创建结果存储图像
    if ( format == "" )
    {
        cout << "没有指定存储图像的格式，默认为GTiff" << endl;
    }
    GDALDriver *poDriver = GetGDALDriverManager()->GetDriverByName( format );
    GDALDataset* reslutDataset = poDriver->Create( this->saveName.c_str(), this->width, this->height, this->bandCount, GDT_Float32, NULL );
    for ( int i = 0; i < this->bandCount; i++ )
    {
        GDALRasterBand* pand = reslutDataset->GetRasterBand( i + 1 );
        pand->RasterIO( GF_Write, 0, 0, this->width, this->height, pResult[i], this->width, this->height, GDT_Float32, 0, 0 );
    }
    GDALClose( reslutDataset );
}

附上处理结果：

 

原始影像

高分辨率全色影像

 

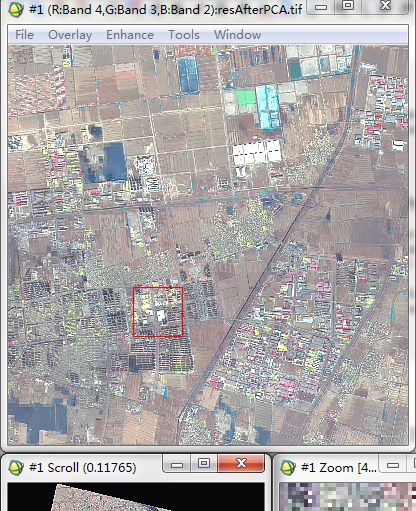
融合结果影像（当然，显示颜色略微与原图有点差异，不过是显示拉伸的问题）

好了，流程就介绍完了，可能代码有点零散，不过大家可能都发现了我这个是写在了一个类里面的，下面我贴出UML的类图，以及这个类的所有代码，供大家使用。

下面是实现代码：

 

// ***********************************************************************
// Author           : Jacory
// Created          : 11-14-2014
//
// Last Modified By : Jacory
// Last Modified On : 11-22-2014
// ***********************************************************************
// 
//     Copyright (c) . All rights reserved.
// 
// 
PCA融合类，实现将多波段遥感图像与全色波段图像进行融合
// 可处理浮点型图像数据
// ***********************************************************************
#pragma once

#include 


class GDALDataset;
class GDALRasterBand;

using namespace std;

class PcaFusion
{
public:
    PcaFusion( string multiFilename, string highRSFilename, string saveName = "" );
    ~PcaFusion( void );
    
    // getter
    string getMultiName() {return multiFilename;};
    string getHighRSName() {return highRSFilename;};
    string getSaveName() {return saveName;};
    const char* getSaveFormat() const { return saveFormat; }
    int getFactor() {return factor;};
    
    // setter
    void setMultiName( string multi );
    void setHighRSName( string highRS );
    void setSaveName( string sName );
    void setSaveFormat( const char* val ) { saveFormat = val; }
    void setFactor( int val );
    
    // 统计波段均值
    double* calMean( GDALDataset* dataset );
    // 求图像矩阵协方差
    double* calCovMatrix( GDALDataset* dataset, double* bandMean );
    // 求实对称矩阵的特征值及特征向量的雅格比法
    bool eejcb( double a[], int n, double v[], double eps, int jt );
    // 矩阵转置
    void transMatrix( double *matrix, int m, int n );
    // 矩阵求逆
    void inverseMatrix( double *matrix, int n );
    // 线性拉伸
    void linearStretch( float** pResult, int width, int height, int bandCount );
    // PCA融合
    bool principalFusion();
    
    void projToRange( float* img, float* ref );
private:
    // PCA变换
    float** PCATransform( float **imgMatrix, double* eigenVector );
    // PCA逆变换
    float** inversePCA( float **imgMatrix, double* eigenVector );
    // 按特征值大小排序特征向量
    void sortEigenVector( double* eigenVector, double* covAfterEejcb );
    // 保存图像
    void saveFile( float** pResult, const char* format = "GTiff" );
    // 得到累积分布函数
    double* cdf( int* h, int length );
    // 直方图匹配
    int* matchHistogram( int* hA, int* hR, int length );
private:
    /// 

    /// 多波段图像路径
    /// 
    string multiFilename;
    /// 

    /// 高分辨率图像路径
    /// 
    string highRSFilename;
    /// 

    /// 保存结果文件路径
    /// 
    string saveName;
    
    /// 

    /// 图像高度
    /// 
    int height;
    /// 

    /// 图像宽度
    /// 
    int width;
    /// 

    /// 图像波段数
    /// 
    int bandCount;
    
    /// 

    /// 保存图像的格式
    /// 
    const char* saveFormat;
    /// 

    /// 多波段图像数据集
    /// 
    GDALDataset* multiDataset;
    /// 

    /// 高分辨率图像数据集
    /// 
    GDALDataset* highResDataset;
    
    /// 

    /// 用于控制直方图匹配精度的系数，从100到10000，值越大，执行速度越慢，默认为100
    /// 
    int factor;
};

 

#include "PcaFusion.h"
#include 
#include "gdal_priv.h"
#include