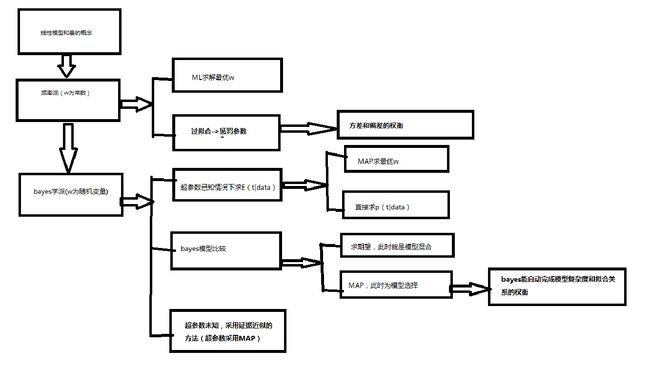
第三章 回归线性模型
Linear models for regression
概念
regression: predict continuous t/t given {x i ,t i ,x new }
linear: linear functions of adjustable parameters
(1)linear funcs of input
(2)fixed non-linear funcs of input->basis funcs
1、linear basis function models
y=wTϕ(x),ϕi(x)=xi,x=(xi)n
以下的应用都可以推广到多项式基、高斯基、sigmoidal基、fourier基等等。
NOTE:多项式基全局性理解->polynomial vs spline
1.1 ML=LS
概率建模: {x}N -> {t}N 的不确定性建模为p(t|x,参数模型)
t=y(x,w)+ ϵ , ϵ∼N(0,β−1) ,需要求解w
那么t~ N(t∣y(x,w),β−1)
P(t1:n)=∏Nn=1N(tn∣y(x,w),β−1)
N(tn∣y(x,w),β−1)=constant×exp(−β×(tn−wTϕ(xn))22)
lnP(t1:n)=−β2×∑Nn=1(tn−wTϕ(xn))2
对w求导:
▽lnP(t1:n)=β2×∑Nn=1(tn−wTϕ(xn))×ϕ(xn)T
令导数=0:
wml=(ϕTϕ)−1ϕTt
NOTE:对行向量求导->对每项求导,组成行向量。
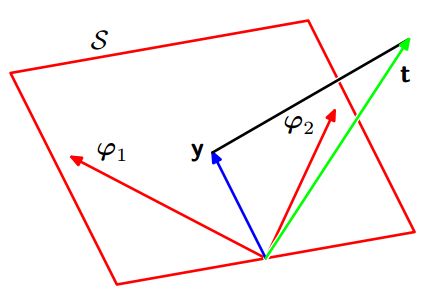
1.2 几何解释
数据N个,基的维度 M<N ,y=(y1…yn).T,t=(t1,…tn).T
而 y=wTϕ(x) ,所以y在 ϕ 所张成的空间里,均方误差最小实质上是t与y的距离最小,也就是当且仅当t垂直于 ϕ 所张成的平面的时候。也就是说y就是t在 ϕ 空间中的正交投影。
如果M>N时候,很可能导致矩阵 ϕTϕ 是奇异的(我猜的,待考虑),这时候 ϕTϕ 中元素值都很大,导致 wML 也很大,称之为degeneracies(退化)。
1.3序列学习 or 在线学习
前面直接求梯度在数据量大的时候不太合适,这里采用随机梯度下降的方法。
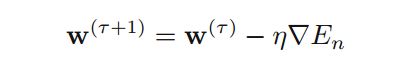
En 表示第n个数据估计值和实际值的均方误差值。就是说每次带入一个点进行迭代,朝着总误差值减小的方向进行,每N次迭代后看w是否不再变化,若否则如此循环迭代。
(推荐:practical optimization,陆吾生)
1.4正则化
NOTE:过拟合->函数过于拟合数据导致扩展性变差。函数过拟合-需要更多的特征-需要更多的非0参数。
因此为了鼓励使用尽可能少的特征(即是更多的参数为0)来描述模型,引入 wTw 作为惩罚项, \lamda 作为惩罚权重。这样就有了下式:
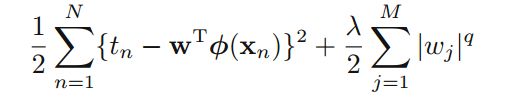
(q=2)
其实只要是为了限制参数,q为多少都可以接受。
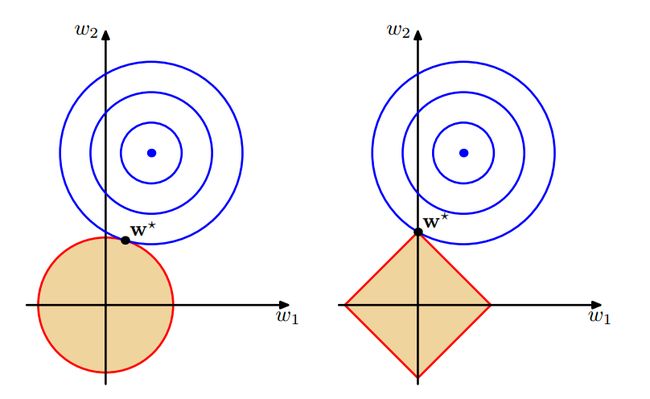
1.5 多输出->decoupling into k independent regression problems
两种方案:
(1)输出视作互相独立的,那么对于每一个输出都有一套基
(2)所有的输出都使用相同的基,只是使用不同的w来计算。
考虑第二种情况:
W的每一列为原来的 w ,对应于t的一个分量

解出来的结果是:
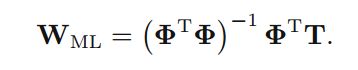
这样得到了与原来相同的结果。w的每一列都有T的对应列决定。
2 bias vs variance
complex models+limited data->overfit(PRML第一章1.1节有实例)
simple models->underfit
正则化->需合适的 λ
本章从两个角度解释这个问题,一个是频率派的角度,一个是贝叶斯派的角度。
NOTE:两个学派的区别在于是否视概率参数是随机变量。
频率学派:bias-variance trade-off
squared loss function:
optimal prediction: 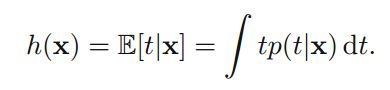
NOTE:区分这里的squared loss function和前面的sum-of-squares error function->这里是由决策理论(第一章)导出,即先定义随机变量损失函数 (y(x,w)−t)2 ,然后对他求期望;而后者是由最大似然估计导出。
L(t−y(x))=(t−y(x))2=(t−h(x)+h(x)−y(x))2
x,t->数据的随机变量
y(x)->未知可能的模型
h(x)->最优模型(E(t|x))
然后带入到SLF里面去,得到
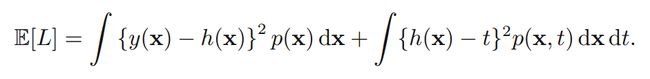
第二项与y(x)无关,即与w无关,仅仅与数据本身有关,因此不考虑;第一项为了使之最小,当然要使y(x)=h(x),然而问题是数据量是有限的,必然导致y(x)无法完整的描述数据,因此会存在一定的差。
所以现在就是要找到这个‘差’的来由,然后去描述它。
贝叶斯观点认为,y(x)之所以无法精确的逼近h(x)是由于w是随机量而不是固定值,也就是说w本身就是不确定的。
而频率派是这样描述的,首先有一个无限大的数据集,我们每次只能选择其中一个样本来处理,因此一个样本导致一个w(对该数据集而言w本身是未知的常量),这才是y(x)无法等于h(x)的原因。
为了描述这种现象,使E(L)的第一项对所有的数据集积分,同时令
(y(x;D)−h(x))2=(y(x;D)−ED[y(x;D)]+ED[y(x;D)]−h(x))2
则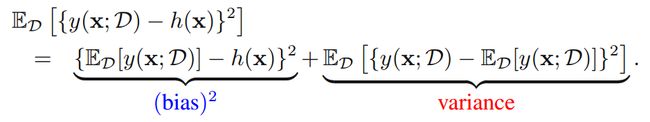
bias表示某个点x在所有数据集上的模型值的平均值与最优值之差;variance表示点x的模型值在所有数据集上的方差。
以上就是频率学派的观点。其最大的局限性在于数据集一般就一个(NOTE:可能有人会说将数据切分成多份,这其实是将相互之间有依赖的数据强行分开,极有可能导致每个数据集对模型的估计更加不精确);其次,在决定惩罚参数 λ ,往往需要进行类似10-fold交叉验证的方式来决定,计算量很大。因此,这就需要寻求新的方法更好解决上述问题。
3 贝叶斯线性模型
前面的ML所应用的模型属于频率学派,这里引入贝叶斯观点,即认为w是随机变量,先验分布是高斯分布。
(NOTE:之所以是高斯,目的是为了使后验概率p(w|t)与先验p(w)形式一致,这称之为共轭性,在prml第二章有论述,其实就是为了计算简便)
(NOTE:mode of guass ->The mode is the value that appears most often in a set of data)
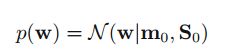

推导过程详见prml 公式(2.116),简单说下,就是 p(w∣t)∝p(t∣w)∗p(w) ,然后按照高斯分布的概率形式归一化前面的系数就可以了。
这里提几点:
(1)与前面ML的联系:首先应用MAP,那么 wmap=mN ;如果p(w)接近均匀分布,即高斯分布的方差无限大,那么 S−10 ->0,此时 mN=wml .
(2)N=0,p(w|t)=p(w)
(3)online : 每来一个data,p(w|t)都可以视作先验带入计算。
(4)下面考察贝叶斯如何控制模型复杂度:
考虑一个简单的高斯先验——0均值各向同性的高斯分布。![]()
(NOTE:一般高斯、对角高斯、各向同性高斯)

此时发现这个式子其实和正则化式子一致。
从(1)和(4)可以看出,只要我们选择合适先验高斯模型,那么最优化这个模型(比如采用map或者ml)时,就能够自动规避过拟合。
(5)下面以一个简单的例子来讨论贝叶斯模型序列化以及模型工作的实质
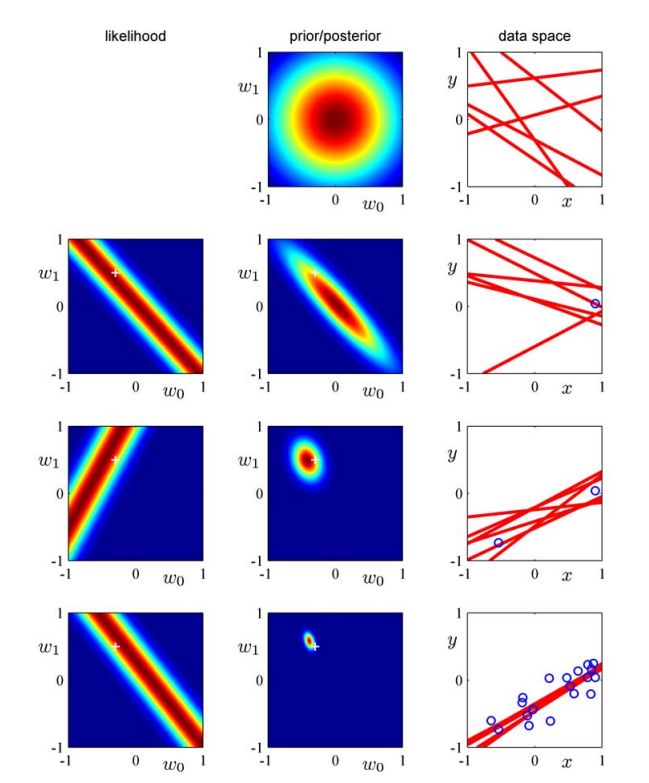
数据产生:f=-0.3+0.5x,x在[-1,1]间均匀采样,然后叠加一个N(0,0.2)噪声。
模型:先验![]() α=2
α=2
序列化过程:第一个数据t1, p(w∣t1)∝p(t1∣w)p(w)
来第二个数据,若整体考虑:
p(w∣t1,t2)∝p(t1,t2∣w)p(w)∝p(t2∣w)p(t1∣w)p(w)∝p(t2∣w)p(w∣t1)
可见如果我们把第一个数据后的后验概率视作为先验,那么新的后验概率就正比于“新的先验”和“新的似然概率”之积。
如图:(r=1, c=2)表示没有数据时先验概率的图;(1,3)表示数据空间中的六个线性模型,该模型参数w取样于(1,2);(2,1)中‘+’表示真实的w值,考虑lnp(t|w)=A-B (t1−w0−w1x1)2 这其实是这个公式的图,当 (t1=w0+w1x1) 显然就是最中间的那条直线;(2,2)中就是(1,2)*(2,1)的结果;(2,3)‘。’表示所观察的数据,可以看到新采样到的w保证了直线都在该数据周围。以下类推,当可观测数据越来越多的时候,模型就越来越精确。
3.2 predictive distribution
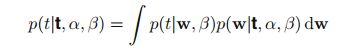
这里观察数据x永远作为条件,因此被忽略。注意到积分中的两个式子都是高斯,根据PRML式子(2.115)结果有:
![]()
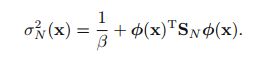
所以从本质上讲,贝叶斯不需要做优化而直接求概率以及期望。
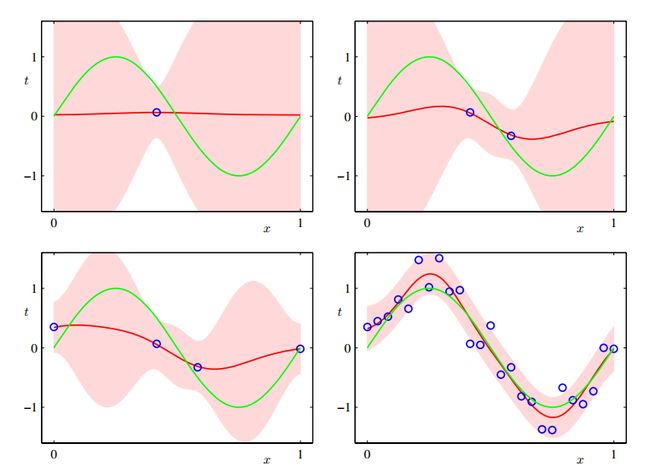
(1,1)图中点作为数据计算w的后验概率得 mN,SN ,绿色直线代表原始sin曲线,红色区域间距代表预测值的方差,红色直线代表预测值的均值。
3.3 equivalent kernel
这一章作为第六章的铺垫,于本章相对独立。
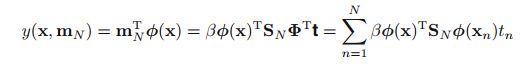
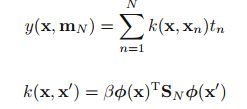
这玩意称之为smoother matrix or equivalent kernel,y(x,m)称之为linear smoothers

解释:局部化
横轴为已知值数据轴 x′ ,纵轴为预测值数据 x 值,z轴为k(x,x’),其中 ϕ 为高斯基。在每一行中,’高斯’中心点总是在x’=x处,反映在右图就是一条45度线。这里称之为localized around x。而这种性质扩展到了非局部的多项式基和sigmoidal基中,如下图。
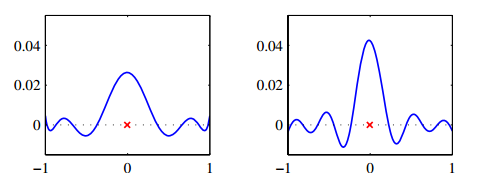
接下来考察预测值y(x)与y(x’)之间的相关性:

这里协方差针对p(w|t),将 ϕ 左右提出,其实就是要求w的方差即 SN 。
可见,如果x与x’越接近,cov就越大,也就说邻近点间的预测是高度相关的。
由此可以想到,是否可以直接定义K而不是 ϕ ,这就是第六章讨论的内容。
此外,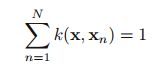 。
。
(NOTE:一个例子,假设所有的 tn=1 ,显然预测y(x)=1,so…)
1.4 贝叶斯模型比较
M:概率分布,由w决定
w:决定M的参数
(NOTE:w决定M,但p(w)!=p(M))
D:观察到的数据,由于x不考虑其概率,可以认为就是指y
model evidence: p(D∣Mi) ,表示不同模型下数据产生的概率
贝叶斯的“不同模型”来源于P( Mi ),简单起见可以假设所有的模型具有相同的先验概率。
首先求出 p(Mi∣D)∝p(Mi)p(D∣Mi)
然后
这里最关键的就是确定 p(D∣Mi) 。这里面没有优化过程,称之为模型平均(也就说对所有的模型加权求平均)。
一种近似的方式是选择一个最好的模型单独预测,这就叫模型选择,那么该选择何种模型呢?在这里可以简化为选择有多少参数的模型呢?或者说模型复杂度是多少?
为了便于分析 p(D∣Mi) ,这里假设M是由一个参数w决定的,那么有:

忽略掉 Mi ,并假设p(w)和p(w|D)如下图:

那么有:
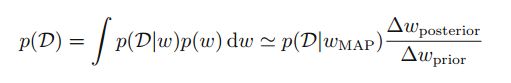
取log后:
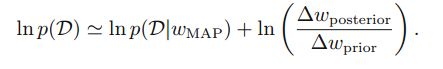
右式第一项表示给定最佳参数 wwap 的log likelihood,在wap情况下其值较大,第二项表示最佳参数下的惩罚度,其值比较小,当然还取决于先验概率。
如果假设模型参数都是条件独立的,那么有下式:

我们选择的模型当然要使证据p(D|M)越大越好,如果M比较大,第一项必然变大(模型拟合的更好),而第二项会变的很小,这就是一个trade-off。
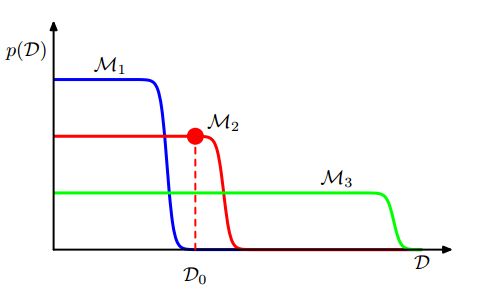
理解这张图:模型越简单,其可以描述的数据集样本就越少,比如y=x,他的数据集样本只能是(1,1…)
等等这种形式,再加上一点噪声;而越复杂的模型其描述的数据集越多,对应的其概率越低。所以 M1 最简单。如果我们有一个数据集 D0 ,从单数据集上讲,我们最佳模型的选择应该是M2。
还有一点,在数据受限的情况下,真实的模型可能比不上错误的模型,比如上述D0数据集,因为考虑到bayes factor ln p(D∣M3)p(D∣M2)<0 ,我们当然选择M2,而实际上由于是很多数据没有给出导致选择错误。
这个时候如果对bayes factor求期望,那么其结果仍然是偏向正确的模型。
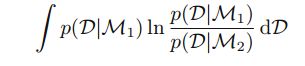
(NOTE1: KL>=0)
(NOTE2:这其实是为了保证bayes理论的正确性,实际上没啥用,因为我事先肯定不知道那个模型是正确的,因此求平均的时候根本不知道对哪个概率求。)
NOTE:贝叶斯局限性:
1、积分难求,对于线性模型或许简单一些,一般情况下预测结果的概率求不出来,这种情况下会使用采样或者近似估计。
2、先验概率选取没有合理的解释
1.5 evidence approximation
(note:empirical Bayes;type2 maximumm likelihood)
在线性模型中,前面还有两个参数 α,β (噪声方差参数和w的先验方差参数),在全bayes观点看来,其实应该视为随机变量,然后求预测值时应该对他们积分,但是这种方式是不可解析的。因此有一种近似的方法,就是通过最大化marginal likelihood function(对w积分去掉w)方法来求 α,β 的点估计。
全贝叶斯预测公式:
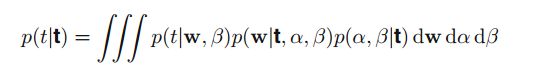
假设 p(α,β∣t) 仅在 α^,β^ 处非常尖锐,那么上式可以简化为:
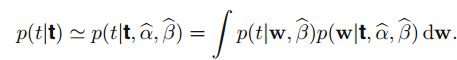
那么现在的问题是如何求 α^,β^
![]()
如果假设 p(α,β) 分布是平坦的,那么最大化后验概率就是最大化似然函数。这样参数的就能直接由训练数据给出。
(NOTE:PRML page166 简介中第二段涉及到Laplace近似,为第四章内容,以后来看)
解决上述方案一个直接的方法是求梯度(1.5.2);然而如果梯度不是闭合的,这时需用到EM算法(PRML第九章)。
1.5.1 评估证据函数(似然函数)
p(t∣α,β)
t:已知的数据x对应的值
α :参数w对应的先验方差参数(当时是简化为 N(0,α−1I) )
β :误差对应分布的精度(方差的倒数)
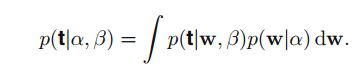
(NOTE: PRML中书里提到一种方法是用高斯线性模型结果2.115来解决这个问题)
这里描述另一种方法,首先给出积分里面的表达式:

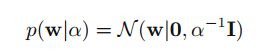
这里假设参数维度是M,条件独立。将与w无关的项提出就有了下式:

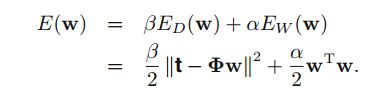
我们看到这个式子是一个二次式,符合高斯指数的特征,所以我要想办法把他化成w的平方形式。
(NOTE: ∫e(x−u)22dx=2π−−√ )
也就是化成
E(w)=β2(tTt−2tTϕw+wTϕTϕw)+α2wTw
对比二次项: βϕTϕ+αI =A
对比一次项: βtTϕw=β2wTϕTt+β2tTϕw=12wTAmN+12mTNAw 所以 mN=βA−1ϕTt
(NOTE: 这里A是一个对称矩阵)
对比常数项: β2t2=E(mN)+12mTNAmN 所以 E(mN)=β2t2−α2mTNmN−β2mTNϕTϕmN
这个和书上P185不一样,why???

(NOTE:后面发现将PRML中3.84带入到3.82,上面这个式子和书上是相等的)
对照多维高斯的定义形式,可以求出积分式:

这样就得到了:
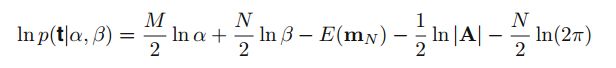
1.5.2 maximizing the evidence function
首先考虑 α ,对上述likelihood求导出现以下几个问题:
(1)|A|怎么求
(2) mN 依赖于alpha,是不是还要对它求导呢
第一个问题:
令![]()
那么A的特征值就是 λi+α ,A的行列式等于其特征值的乘积。故而
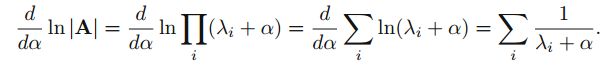
上述求导的结果是:
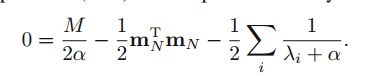
这里并没有对 mN 求导,作者的意图是先将 mN 视作一个单独的参数,求出 α 后带入求 mN ,然后反过来再求 α ,如此反复迭代。(不知道这样做的原理)

这样 α 就求出来了,然而无论是分子还是分母都是依赖于 α ,作者意指固定点迭代。
然后求 β ,

1.5.3 参数的有效个数
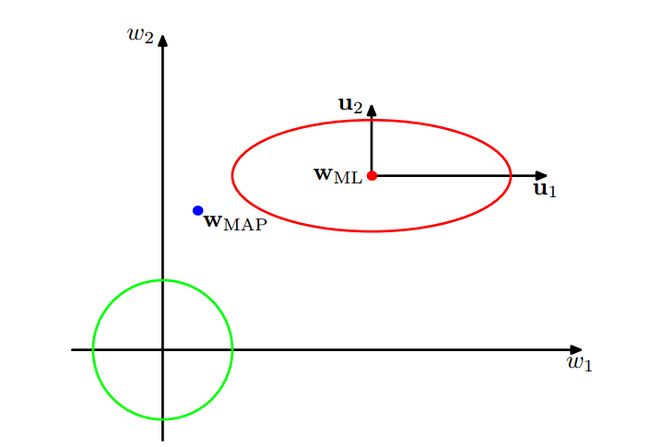
这里考察 γ 这个量的意义。上图其实描述的是 p(w),p(t∣w) 这两个式子的图(NOTE:书里现在讲的evidence是指 p(t∣w) )。这里假设 p(t∣w) 仅有两个参数,假设 λ1,2 .
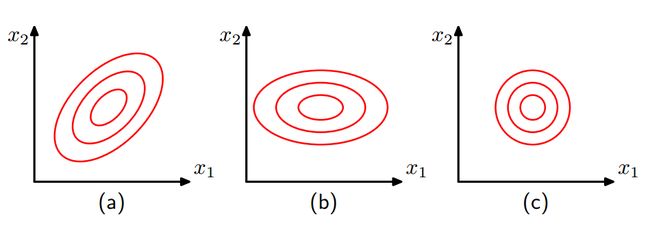
我们知道 p(t∣w) 是高斯形式,其协方差矩阵就是A,因此 λi 是对应的特征值。假设 λi 对应 wi (这里已经将参数空间旋转使之与特征向量平行,所以这里的w可能和前面的w不太一样,但是个数是不变的)。如果 λi>>α ,那么 λλ+α=1 代表的意义是证据函数在 wi 这个方向变化变化较大,称之为well determined参数;反之 λλ+α=0 ,意指证据函数在这个方向上变化较小,不需要这个特征,如图在u1方向上变化就较大而在u2上较小。再考察 γ 的表达式,其实就是统计well determined参数的个数,这就是 γ 的意义。
(NOTE:这个图感觉和书上实际举例有一点冲突,感觉应该将椭圆旋旋或者wap点在右下比较合理)
(NOTE:高斯协方差矩阵的特征向量正交?)
对参数beta的理解:
对比下面两个式子:
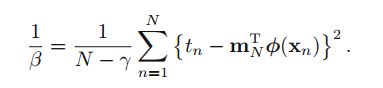

第一个式子是上节推导的结果的方差,第二个式子是最开始用ML直接推导的结果的方差。
两个相差一个 γ 。
首先解释一下自由度:是指当以样本的统计量来估计总体的参数时,样本中独立或能自由变化的数据的个数称为该统计量的自由度。
先看下面两个式子:

上面式子是方差有偏估计,下面是无偏的。注意到其实是因为样本均值的存在减少了1个自由数据的自由度导致的。(NOTE:书上说是因为拟合噪声导致的,不太好理解)
同理,由于在bayes估计中,发现有 γ 个有效参数,必然导致在估计方差时要降低 γ 个自由度。
(NOTE:假想数据t,x与w构成了N个方程,由于有效个数为 γ ,因此实际能用上的数据为 γ 个,所以自由变化的就是N- γ 了)
现在仍然举第一章1.1节的例子,采用sin数据,M=10,假定 β 已经是优化值了
(NOTE:这里有两张图还要研究)
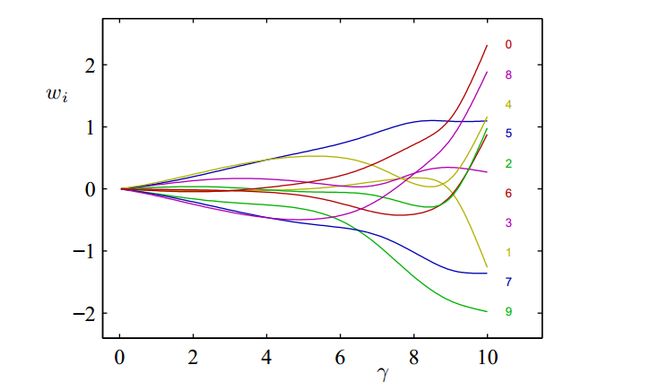
1.6 固定基函数的局限
前面的线性模型有很多优点,参数线性使得该模型有闭式解,而且bayes模型也是可解析的;能够通过基的选择解决大量非线性问题。但是存在以下两个缺点:
(1)基是固定的,而且在建模之前要选择好:比如多项式基选择很可能导致结果拟合的不好
(2)维数灾难:指随着数据维度升高,建模复杂度以指数形式增长。
比如:多项式基,数据维度为M时,若以3次建模,则需要O( M3 ),这里当然不是指数增长,但是仍然增长非常快,以至计算困难。
解决方案:降维
(1)数据x本身是高度相关的
(2)预测值y仅仅依赖于部分x