条件异方差模型
方差齐性变换为异方差序列的精确拟合提供了一种很好的解决方法。但是这种方法只适用部分异方差波动序列。因为要使用方差齐性变换必须事先知道异方差函数的形式,而这不是对所有的序列都可以做到的。实践中,我们只能根据残差图及残差平方图所显示出来的特点,使用一些常用的函数形式估计异方差函数。
在进行金融时间序列分析时,由于金融序列的标准差与水平之间通常具有某种正相关关系,这导致对数变化在金融时间序列中普遍采用。
但大量的实践证明这种假设太单一化了,对数变化通常只适用于方差随均值的变化而变化的部分序列。异方差的特征有很多,我们不能通过对数变换将所有的异方差序列转化成方差齐性序列。
这里介绍一种在金融领域广泛采用的异方差处理方法:条件异方差模型。
ARCH模型
一、集群效应
在宏观经济领域和金融领域,经常可以看到具有如下特征的时间序列:它们在消除确定性非平稳因素的影响之后,残差序列的波动在大部分时段是平衡的,但是会在某些时段波动持续偏大,在某些时段波动持续偏小,呈现出集群效应(volatility cluster).
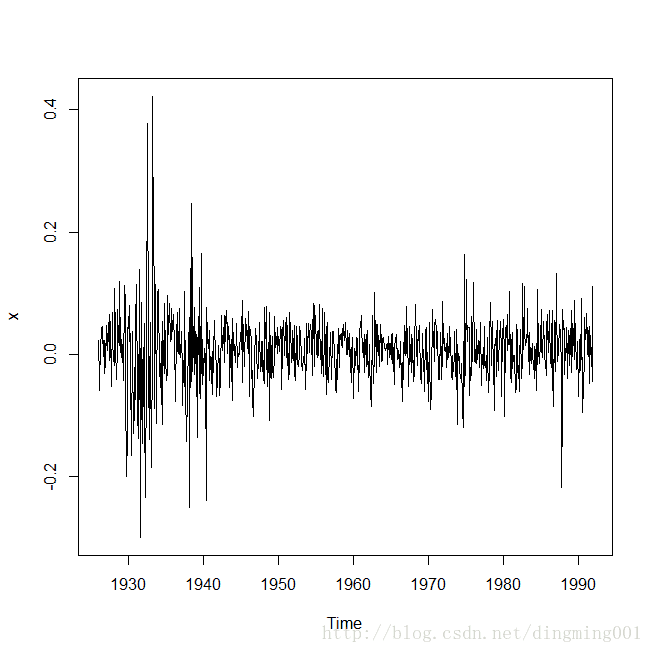
考察1926年到1991年标准普尔500股票价值加权月度收益率序列的集群效应特征。
k<-read.table("D:/R-TT/book4/4R/data/file22.csv",sep=",",header = T)
x<-ts(k$returns,start = c(1926,1),frequency = 12)
plot(x)#绘制序列平方图
plot(x^2)
标准普尔500股票价值加权月度收益率序列平方图
考察该序列时序图,时序图显示该序列没有显著的非平稳特征,序列在0仠附近波动,大部分时期波动范围在-0.1到+0.1之间,但是在一些特殊时段,序列的波动很大,这就是集群效应特征。
集群效应意味着在整个序列观察期,序列的方差基本是齐性的,但是是某一段或者某几段时期方差却显著异于期望方差。这时需要引入条件异方差模型。
ARCH模型的结构
ARCH模型的全称是自回归条件异方差模型,有时简称为条件异方差模型。
考察异方差函数的自相关性:
(1)自相关系数恒为零
(2)存在某个自相关系数不为零,构造q阶自回归条件异方差模型,ARCH(q)
ARCH模型的作用
ARCH模型的实质是将历史波动条件信息作为条件,并采用某种自回归形式来刻画波动的变化,对于一个时间序列而言,在不同的时刻包含的历史信息不同,因而相应的条件方差也不同。利用ARCH模型可以刻画出随时间变化而变化的条件方差,它比无条件方差更及时的反映了序列即期波动的特征, 这就是ARCH模型的作用。
它和前面介绍的ARIMA模型、残差自回归模型、确定性因素分析分解模型是两种性质的模型,它关注的是序列的波动性拟合。
拿到一个观察值序列后,完整的分析应该关注水平和波动两个方面,我们通常会首先提取序列的水平相关信息,然后分析残差中蕴涵的波动相关信息。将这两方面的信息综合起来才是比较完整和精确分析结果。
####ARCH检验
要拟合ARCH模型,首先需要进行ARCH检验。ARCH检验是一种特殊的异方差检验,它不仅要求序列具有异方差性,而且要求这种异方差性是由某种自相关关系造成,这种自相关关系可以用残差的自回归模型进行拟合。
常用的方法是Portmanteau Q 检验和 LM检验
1.Portmanteau Q 检验
该方法的构造思想是:如果残差序列方差非齐,且具有集群效应,那么残差平方序列通常具有自相关性,所以方差非齐性检验可以转化成残差平方序列的自相关性检验。
H0:残差平方序列纯随机
H1:残差平方序列自相关
当Q(q)检验统计量的p值小于显著水平a时,拒绝原假设,认为该序列方差非齐性具有自相关性。
2. LM检验
拉格朗日乘子检验。构造思想:如果残差序列方差非齐,具有集群效应,那么残差平方序列且有自相关性。那么我们尝试使用自回归模型(ARCH(q)模型)拟合残差平方序列。于是方差齐性检验就可以转化成是否具有显著性成立的检验。
H0:残差平方序列纯随机
H1:残差平方序列具有自相关性
当LM(q)检验统计量的p值小于显著性水平a时,拒绝原假设,认为该序列方差非齐,并且可以用q阶自回归模型拟合残差平方序列中自相关关系。
在R语言中做拉格朗日乘子检验之前,需要先下载FTS程序包,并用library函数调用该包。 在这个包里有一个ArchTest函数做LM检验。而Portmanteau Q检验其实就是对残差平方序列进行纯属随机性检验。所以对残差平方序列进行纯随机性检验。所以对残差序列进行平方运算之后,只要调用Box.test函数就可以完成Portmanteau Q检验。
拟合ARCH模型可以调用tseries包中的garch函数,garch函数的命令格式为:
garch(x,order=)
-x:序列名
-order:拟合模型阶数
(1)拟合ARCH(q)模型为 order = c(0,q)
(2)拟合GARCH(p,q)模型为 order = c(p,q)
对1926-1991年标准普尔500股票价值加权月度收益率序列进行ARCH检验,并拟合该序列的特征波动。
> library(zoo)
> library(FinTS)
> for(i in 1:5) print(ArchTest(x,lag=i))
ARCH LM-test; Null hypothesis: no ARCH effects
data: x
Chi-squared = 55.521, df = 1, p-value = 9.248e-14
ARCH LM-test; Null hypothesis: no ARCH effects
data: x
Chi-squared = 68.292, df = 2, p-value = 1.443e-15
ARCH LM-test; Null hypothesis: no ARCH effects
data: x
Chi-squared = 87.129, df = 3, p-value < 2.2e-16
ARCH LM-test; Null hypothesis: no ARCH effects
data: x
Chi-squared = 87.282, df = 4, p-value < 2.2e-16
ARCH LM-test; Null hypothesis: no ARCH effects
data: x
Chi-squared = 87.492, df = 5, p-value < 2.2e-16> #Portmanteau Q检验
> for(i in 1:5) print(Box.test(x^2,lag=i))
Box-Pierce test
data: x^2
X-squared = 55.545, df = 1, p-value = 9.137e-14
Box-Pierce test
data: x^2
X-squared = 85.09, df = 2, p-value < 2.2e-16
Box-Pierce test
data: x^2
X-squared = 126.06, df = 3, p-value < 2.2e-16
Box-Pierce test
data: x^2
X-squared = 138.74, df = 4, p-value < 2.2e-16
Box-Pierce test
data: x^2
X-squared = 141.9, df = 5, p-value < 2.2e-16LM检验和Q检验都显示该序列显著方差非齐,且残差平方序列具有显著自相关,可以用ARCH模型提取残差平方序列中蕴涵的相关关系。而LM检验和Q检验都显示1阶至5阶ARCH模型均显著成立,这说明残差平方序列具有长期相关,ARCH(q)模型的阶数q将会比较大。本例尝试拟合ARCH(5)和ARCH(4).
> library(tseries)
> x.fit<-garch(x,order=c(0,5))
summary(x.fit)
Call:
garch(x = x, order = c(0, 5))
Model:
GARCH(0,5)
Residuals:
Min 1Q Median 3Q Max
-6.3060 -0.4211 0.1695 0.7381 4.5386
Coefficient(s):
Estimate Std. Error t value Pr(>|t|)
a0 1.156e-03 8.348e-05 13.853 < 2e-16 ***
a1 4.750e-02 3.147e-02 1.509 0.131
a2 2.014e-01 2.417e-02 8.333 < 2e-16 ***
a3 2.203e-01 4.793e-02 4.596 4.30e-06 ***
a4 2.006e-01 4.360e-02 4.600 4.23e-06 ***
a5 1.243e-02 3.388e-02 0.367 0.714
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Diagnostic Tests:
Jarque Bera Test
data: Residuals
X-squared = 404.86, df = 2, p-value < 2.2e-16
Box-Ljung test
data: Squared.Residuals
X-squared = 0.0306, df = 1, p-value = 0.8611
有参数不显著,降阶处理
library(tseries)
x.fit<-garch(x,order=c(0,4))
summary(x.fit)
Call:
garch(x = x, order = c(0, 4))
Model:
GARCH(0,4)
Residuals:
Min 1Q Median 3Q Max
-6.2693 -0.4193 0.1683 0.7407 4.5441
Coefficient(s):
Estimate Std. Error t value Pr(>|t|)
a0 1.175e-03 8.276e-05 14.193 < 2e-16 ***
a1 4.955e-02 2.936e-02 1.688 0.0914 .
a2 2.011e-01 2.393e-02 8.402 < 2e-16 ***
a3 2.175e-01 4.715e-02 4.612 3.98e-06 ***
a4 2.054e-01 4.195e-02 4.897 9.74e-07 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Diagnostic Tests:
Jarque Bera Test
data: Residuals
X-squared = 395.67, df = 2, p-value < 2.2e-16
Box-Ljung test
data: Squared.Residuals
X-squared = 0.020552, df = 1, p-value = 0.886还是有参数不显著,接着降阶。
library(tseries)
x.fit<-garch(x,order=c(0,3))
summary(x.fit)
Call:
garch(x = x, order = c(0, 3))
Model:
GARCH(0,3)
Residuals:
Min 1Q Median 3Q Max
-6.2420 -0.3985 0.1671 0.7501 4.4193
Coefficient(s):
Estimate Std. Error t value Pr(>|t|)
a0 1.437e-03 6.903e-05 20.809 < 2e-16 ***
a1 7.954e-02 2.821e-02 2.820 0.0048 **
a2 2.231e-01 2.587e-02 8.624 < 2e-16 ***
a3 2.732e-01 4.384e-02 6.232 4.61e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Diagnostic Tests:
Jarque Bera Test
data: Residuals
X-squared = 585.27, df = 2, p-value < 2.2e-16
Box-Ljung test
data: Squared.Residuals
X-squared = 8.8831e-06, df = 1, p-value = 0.9976
参数显著并通过检验。
#绘制条件异方差模型拟合的95%置信区间
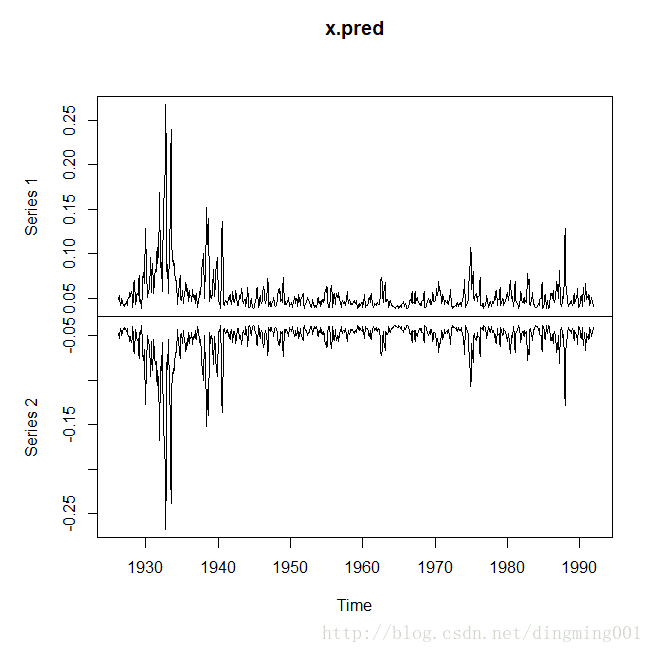
x.pred<-predict(x.fit)
plot(x.pred)#条件异方差置信区间和方差齐性置信区间比较图示
plot(x)
lines(x.pred[,1],col=2)
lines(x.pred[,2],col=2)
abline(h=1.96*sd(x),col=4,lty=2)
abline(h=-1.96*sd(x),col=4,lty=2)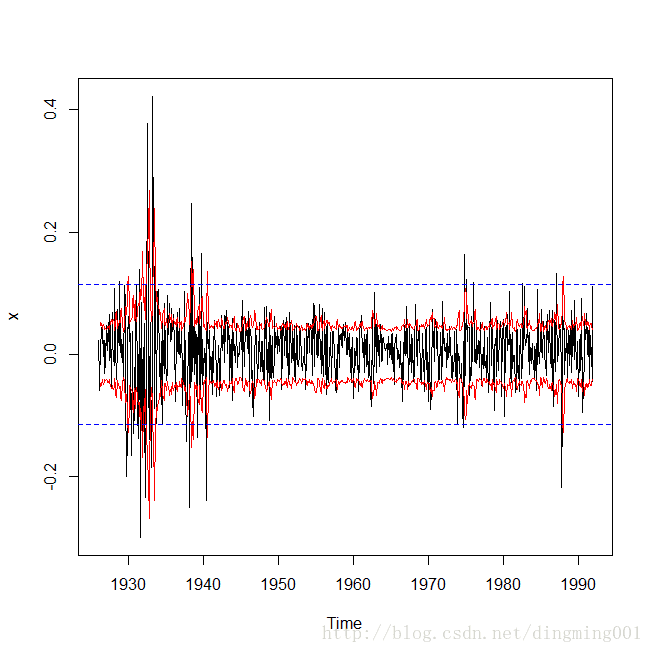
条件异方差置信区间和方差齐性置信区间比较图示
上图给出了条件异方差模型拟合的95%置信区间的范围,考虑到原序列的波动特征,显然条件异方差模型更好的拟合了原序列的集群效应波动特征,显示条件异方差模型拟合的置信区间比无条件方差两条平行线给出95%置信区间更加符合原序列的真实波动情况,这说明条件异方差模型对序列波动的预测将会更加准确。