深度强化学习研究笔记(2)——Q-learning(Q-learning问题描述,Q-table方法,一个Python小例子)
文章目录
- 1. Q-learning问题描述
- 2. Q-learning的一种典型实现方法及示例(Q-table查表法)
- 3. 利用Q-learning得到的Q-table进行验证(让agent独立行走)
- 4. 代码实现(Python 2和Python 3均支持)
- 5. 小结
1. Q-learning问题描述
Q-learning是一种典型的基于价值(Value)函数的强化学习方法,其中的Q是一个数值(可以理解为价值value),通常在初始化时有可能被赋予一个任意数值(因问题场景而异),在迭代时刻 t t t,我们有状态 s t s_t st,此时代理做出动作 a t a_t at,然后得到奖励 r t r_t rt,从而进入到一个更新的状态 s t + 1 s_{t+1} st+1,从而Q值得到更新,其更新公式为:
(1) Q ( s t , a t ) ← ( 1 − α ) ⋅ Q ( s t , a t ) ⎵ old value + α ⎵ learnig rate ⋅ ( r t ⎵ reward + γ ⎵ discount factor ⋅ max a Q ( s t + 1 , a ) ⎵ estimate of optimal future value ) ⏞ learned value Q\left( {{s_t},{a_t}} \right) \leftarrow \left( {1 - \alpha } \right) \cdot \underbrace {Q\left( {{s_t},{a_t}} \right)}_{{\text{old}}\;{\text{value}}} + \underbrace \alpha _{{\text{learnig}}\;{\text{rate}}} \cdot \overbrace {\left( {\underbrace {{r_t}}_{{\text{reward}}} + \underbrace \gamma _{{\text{discount}}\;{\text{factor}}} \cdot \underbrace {\mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right)}_{{\text{estimate}}\;{\text{of}}\;{\text{optimal}}\;{\text{future}}\;{\text{value}}}} \right)}^{{\text{learned}}\;{\text{value}}} \tag {1} Q(st,at)←(1−α)⋅oldvalue Q(st,at)+learnigrate α⋅⎝⎜⎜⎛reward rt+discountfactor γ⋅estimateofoptimalfuturevalue amaxQ(st+1,a)⎠⎟⎟⎞ learnedvalue(1)
从上述公式可以看出,Q值的更新相当于利用学习率对过去的Q值和当前的Q值进行加权求和。
(注: 关于学习率设定,有的资料会考虑历史学习的结果,即学习率小于1;也有的资料并未考虑历史学习的结果,相当于学习率设置为1)
注: 上式中,可能有同学会对右边括号中的 r t r_t rt写法有困惑(有的资料里面用 r t r_t rt表示,有的资料里面用 r t + 1 r_{t+1} rt+1表示,其实它们的含义是一样的,都可以。如果是 r t r_t rt,这里的奖励指的是在状态 s t s_t st已发生的条件下采取动作之后得到的奖励;如果是 r t + 1 r_{t+1} rt+1,则表示在采取动作到达状态 s t + 1 s_{t+1} st+1得到的奖励。两者含义一样,只是约定的规则不同而已。)
令 λ = γ / α \lambda=\gamma / \alpha λ=γ/α,将上述公式(1)的右边进行同类项合并,可得:
(2) Q ( s t , a t ) ← ( 1 − α ) ⋅ Q ( s t , a t ) + α ⋅ r t + γ ⋅ max a Q ( s t + 1 , a ) ← Q ( s t , a t ) + α ⋅ r t + γ ⋅ max a Q ( s t + 1 , a ) − α ⋅ Q ( s t , a t ) ← Q ( s t , a t ) + α ⋅ ( r t + γ α ⋅ max a Q ( s t + 1 , a ) − Q ( s t , a t ) ) ← Q ( s t , a t ) + α ⋅ ( r t + λ ⋅ max a Q ( s t + 1 , a ) − Q ( s t , a t ) ) \begin{aligned} Q\left( {{s_t},{a_t}} \right) &\leftarrow \left( {1 - \alpha } \right) \cdot Q\left( {{s_t},{a_t}} \right) + \alpha \cdot {r_t} + \gamma \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) \\ &\leftarrow Q\left( {{s_t},{a_t}} \right) + \alpha \cdot {r_t} + \gamma \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) - \alpha \cdot Q\left( {{s_t},{a_t}} \right) \\ &\leftarrow Q\left( {{s_t},{a_t}} \right) + \alpha \cdot \left( {{r_t} + \frac{\gamma }{\alpha } \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) - Q\left( {{s_t},{a_t}} \right)} \right) \\ &\leftarrow Q\left( {{s_t},{a_t}} \right) + \alpha \cdot \left( {{r_t} + \lambda \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) - Q\left( {{s_t},{a_t}} \right)} \right) \\ \end{aligned} \tag {2} Q(st,at)←(1−α)⋅Q(st,at)+α⋅rt+γ⋅amaxQ(st+1,a)←Q(st,at)+α⋅rt+γ⋅amaxQ(st+1,a)−α⋅Q(st,at)←Q(st,at)+α⋅(rt+αγ⋅amaxQ(st+1,a)−Q(st,at))←Q(st,at)+α⋅(rt+λ⋅amaxQ(st+1,a)−Q(st,at))(2)
根据强化学习中贝尔曼(Bellman)方程的定义,我们有:
(3) r t + λ ⋅ max a Q ( s t + 1 , a ) = Q ( s t + 1 , a t ) {r_t} + \lambda \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) = Q\left( {{s_{t + 1}},a_{t}} \right) \tag {3} rt+λ⋅amaxQ(st+1,a)=Q(st+1,at)(3)
将上述公式(3)代入公式(2),可得:
(4) Q ( s t , a t ) ← Q ( s t , a t ) + α ⋅ ( Q ( s t + 1 , a t ) − Q ( s t , a t ) ) Q\left( {{s_t},{a_t}} \right) \leftarrow Q\left( {{s_t},{a_t}} \right) + \alpha \cdot \left( {Q\left( {{s_{t + 1}},a_{t}} \right) - Q\left( {{s_t},{a_t}} \right)} \right) \tag {4} Q(st,at)←Q(st,at)+α⋅(Q(st+1,at)−Q(st,at))(4)
若进一步简化,将学习率 α \alpha α设置为1(即不考虑过去求解的价值),且又因为 λ = γ / α = γ / 1 = γ \lambda=\gamma / \alpha=\gamma / 1=\gamma λ=γ/α=γ/1=γ,所以上式可以写成:
(5) Q ( s t , a t ) ← Q ( s t + 1 , a t ) ← r t + λ ⋅ max a Q ( s t + 1 , a ) ← r t + γ ⋅ max a Q ( s t + 1 , a ) \begin{aligned} Q\left( {{s_t},{a_t}} \right) &\leftarrow Q\left( {{s_{t + 1}},{a_t}} \right) \\ &\leftarrow {r_t} + \lambda \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) \\ & \leftarrow {r_t} + \gamma \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) \end{aligned} \tag {5} Q(st,at)←Q(st+1,at)←rt+λ⋅amaxQ(st+1,a)←rt+γ⋅amaxQ(st+1,a)(5)
可以看出,在这种简化的场景下,变量 γ \gamma γ与变量 λ \lambda λ是等效的,这也是为什么有的资料在算法描述中会用 γ \gamma γ来表示学习率,有的资料用 λ \lambda λ来表示学习率的原因。基于上述公式(5),Q-learning的training算法描述如下所示:
Set the γ \gamma γ parameter, and environment rewards in matrix R R R
Initialize matrix Q Q Q to zeros
for each episode
Select a random initial state s s s
while the goal state hasn’t been reached do
Select one action a a a among all possible actions for the current state
Using this possible action a a a, consider going to the next state s t + 1 s_{t+1} st+1
Get maximum Q Q Q value for this next state s t + 1 s_{t+1} st+1 based on all possible actions
Compute: Q ( s t , a t ) ← Q ( s t + 1 , a t ) Q\left( {{s_t},{a_t}} \right) \leftarrow Q\left( {{s_{t + 1}},{a_t}} \right) Q(st,at)←Q(st+1,at)
Update state: s t ← s t + 1 s_{t} \leftarrow s_{t+1} st←st+1
end while
end for
从上述算法可以看出,在迭代过程中,奖励矩阵 R R R是设置为不变的。
2. Q-learning的一种典型实现方法及示例(Q-table查表法)
这里我们用一个经典示例Path-finding来说明Q-learning算法。如下图所示,有一个一组房间,每隔房间的编号为0~4,其中有的房间之间能够互通,有的不能互通,5号区域为室外。如下图所示:
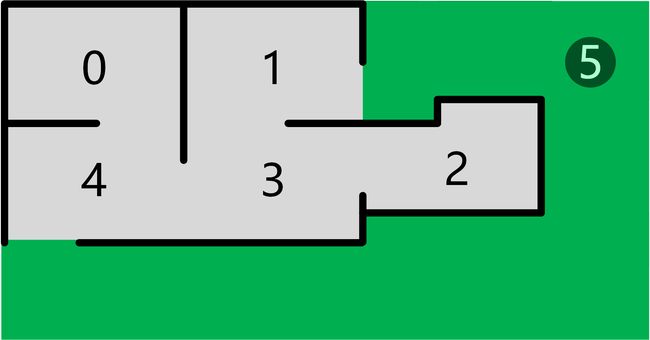
我们期望把Agent放在任何房间,然后它自己能够从那个房间走出大楼(换句话说,目标房间是5号)。
现在,我们构造一个连通图,并约定:能够直接到达5号区域的边,其奖励值为100(包括5号自己到达5号);房间之间彼此连通的边,其奖励值为0;房间之间彼此阻隔的边,其奖励值为-1;房间自己到达自己的边,其奖励值为-1。根据这样的规则,我们可以构造如下连通图(对于互相阻隔的房间,它们之间的边被省略了):
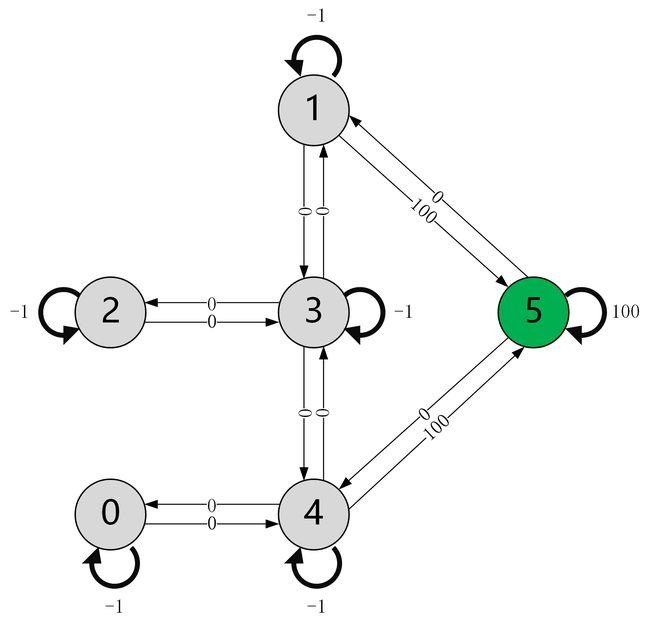
定义state和action。我们约定将代理当前所在的区域编号作为state,将代理前往哪一个区域的编号作为action。根据上述连通图中的奖励值,我们可以根据上述连通图构造奖励矩阵 R R R,如下图所示:
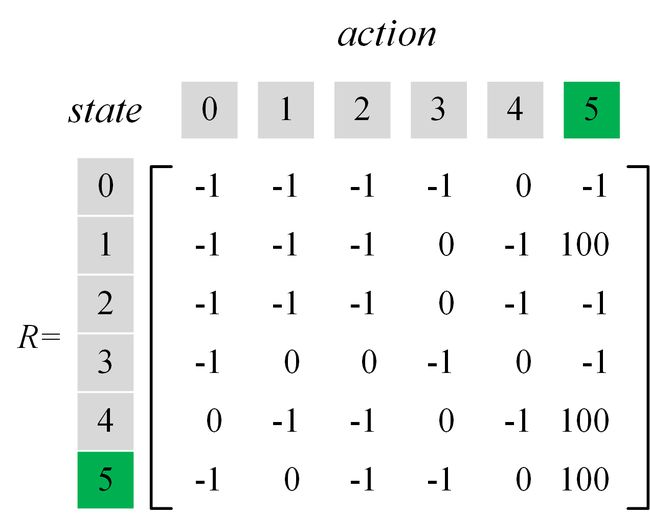
此时我们再创建一张Q-table,对其进行初始化,将内部所有元素置为0,如下图所示:
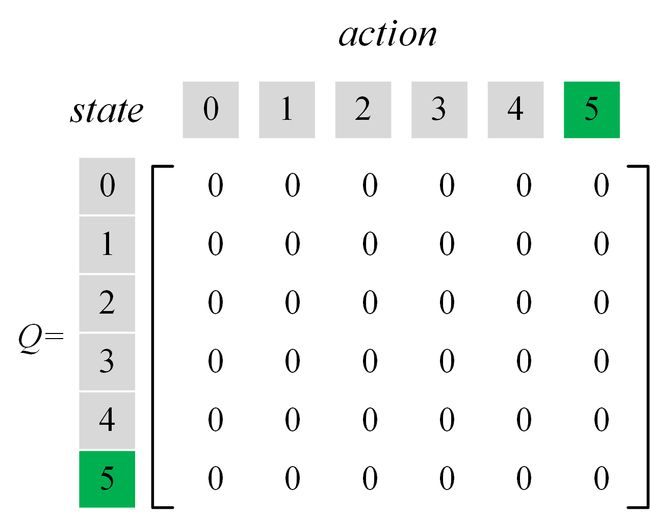
回顾公式(5),后续将利用该公式对 Q Q Q值进行更新(设定 γ \gamma γ的值为 0.8 0.8 0.8):
(5) Q ( s t , a t ) ← r t + γ ⋅ max a Q ( s t + 1 , a ) Q\left( {{s_t},{a_t}} \right) \leftarrow {r_t} + \gamma \cdot \mathop {\max }\limits_a Q\left( {{s_{t + 1}},a} \right) \tag {5} Q(st,at)←rt+γ⋅amaxQ(st+1,a)(5)
假定代理当前位于1号房间,查询奖励矩阵 R R R,代理可以到达区域3和区域5,现在随机选择一个动作“前往区域3”,我们通过查询Q-table来更新 Q Q Q值(具体地,是更新元素 Q ( 1 , 3 ) Q(1,3) Q(1,3)),此时,需要查表获得两类数据:
- 奖励(Reward)。这里特指“从房间1(当前state)前往房间3(采取的action)所获得的即时奖励”,因此需要查询的数据为 R ( 1 , 3 ) R(1,3) R(1,3)。
- 未来的价值(Value)。这里特指“进入房间3后(next state)所能获得的最大即时奖励”,因此需要查询的数据为: Q ( 3 , 1 ) Q(3,1) Q(3,1)、 Q ( 3 , 2 ) Q(3,2) Q(3,2)和 Q ( 3 , 4 ) Q(3,4) Q(3,4)。
进一步,根据公式(5)可知当前 Q Q Q值的更新算式如下:
(6) Q ( 1 , 3 ) ← R ( 1 , 3 ) + 0.8 ⋅ max ( Q ( 3 , 1 ) , Q ( 3 , 2 ) , Q ( 3 , 4 ) ) ← 0 + 0.8 ⋅ max ( 0 , 0 , 0 ) ← 0 \begin{aligned} Q\left( {1,3} \right) &\leftarrow R\left( {1,3} \right) + 0.8 \cdot \max \left(Q\left( {3,1} \right), Q\left( {3,2} \right), Q\left(3,4 \right) \right) \\ & \leftarrow 0 + 0.8 \cdot \max \left( 0, 0, 0 \right) \\ & \leftarrow 0 \end{aligned} \tag {6} Q(1,3)←R(1,3)+0.8⋅max(Q(3,1),Q(3,2),Q(3,4))←0+0.8⋅max(0,0,0)←0(6)
查表过程如下图所示:
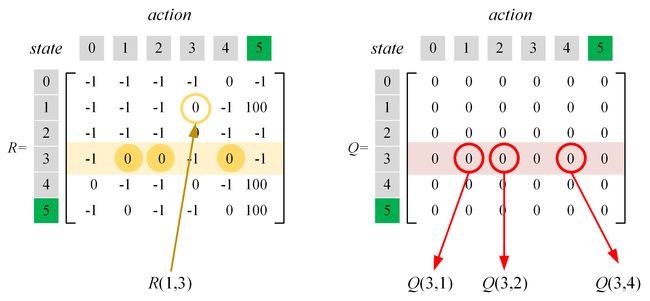
至此,Q-table完成一次更新。更新后,state为区域3,它对应前面算法描述中的一次while内部循环。更新后的数据如下图所示(数据暂时没有变化):

现在,我们进行算法while内部的第二次循环,在第一次循环时随机采用的action是“前往区域3”,现在还可以选择action“前往区域5”,根据公式(5),可知当前 Q Q Q值的更新算式如下:
(7) Q ( 1 , 5 ) ← R ( 1 , 5 ) + 0.8 ⋅ max ( Q ( 5 , 1 ) , Q ( 5 , 4 ) , Q ( 5 , 5 ) ) ← 100 + 0.8 ⋅ max ( 0 , 0 , 0 ) ← 100 \begin{aligned} Q\left( {1,5} \right) &\leftarrow R\left( {1,5} \right) + 0.8 \cdot \max \left(Q\left( {5,1} \right),Q\left( {5,4} \right), Q\left( {5,5} \right) \right) \\ & \leftarrow 100 + 0.8 \cdot \max \left( 0, 0, 0 \right) \\ & \leftarrow 100 \end{aligned} \tag {7} Q(1,5)←R(1,5)+0.8⋅max(Q(5,1),Q(5,4),Q(5,5))←100+0.8⋅max(0,0,0)←100(7)
查表过程不再赘述。至此,Q-table完成又一次更新,更新后的state是区域5,它对应前面算法描述中的一次while内部循环。更新后的数据如下图所示(此时发生了变化):
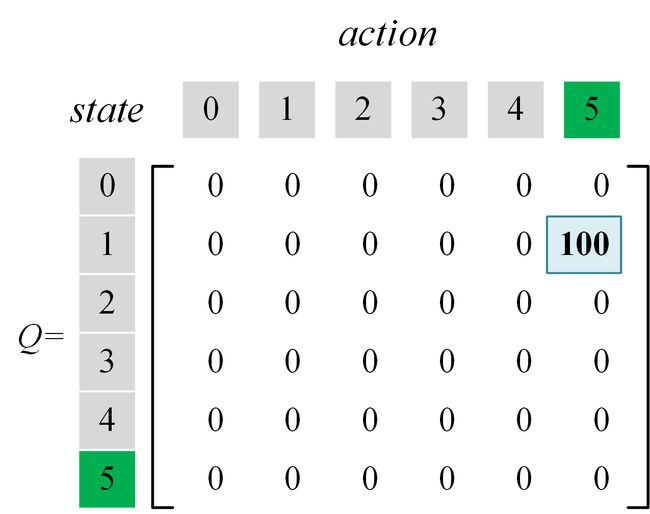
由于当前的state是区域5,已经到达了目标,于是可以退出while循环,进行下一次episode。
注: 在迭代的过程中,由于while循环中的动作选择是随机的,因此在迭代过程中的Q-table可能会有所不同(本笔记特意选择了不一样的动作,方便与其他资料进行对照比较,e.g, https://zhuanlan.zhihu.com/p/29213893 ),但最终得到的Q-table是相同的。
接下来按照上述思路不断进行迭代,最终得到的Q-table如下所示:
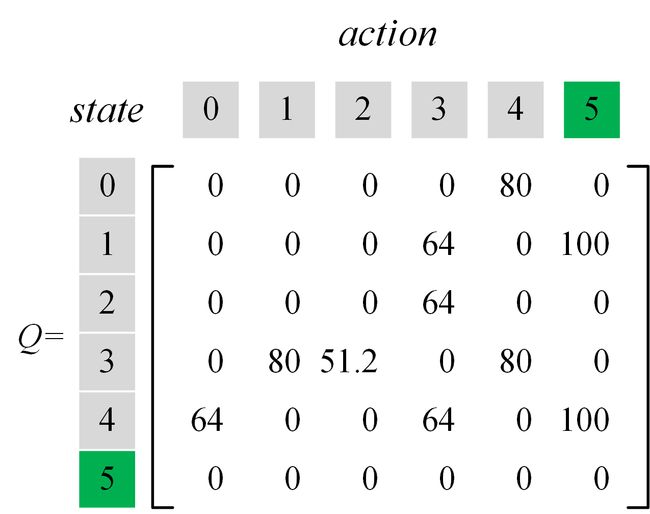
3. 利用Q-learning得到的Q-table进行验证(让agent独立行走)
在得到了Q-table后,我们就可以根据该矩阵让代理独自行走寻找路径了。主要思想是查找当前位置具有最大 Q Q Q值的action,然后执行,如此反复,直到到达目的地为止。具体算法如下:
Initialize state s s s
while the goal state hasn’t been reached do
Choose an action a a a which has the max Q Q Q value in Q-table corresponding to current s s s
Update state s s s by execution the choosed action a a a
end while
4. 代码实现(Python 2和Python 3均支持)
基于Python的完整单文件代码如下所示(代码出处:https://zhuanlan.zhihu.com/p/29213893):
import numpy as np
import random
# Build Q-table
q = np.zeros((6, 6))
q = np.matrix(q)
# Build R-table
r = np.array([[-1, -1, -1, -1, 0, -1], [-1, -1, -1, 0, -1, 100], [-1, -1, -1, 0, -1, -1], [-1, 0, 0, -1, 0, -1],
[0, -1, -1, 0, -1, 100], [-1, 0, -1, -1, 0, 100]])
r = np.matrix(r)
# Discount factor
gamma = 0.8
# Training
for i in range(1000):
# For each training episode, randomly select a state
state = random.randint(0, 5)
while state != 5:
# Select the action of a non-negative value in the R-table
r_pos_action = []
for action in range(6):
if r[state, action] >= 0:
r_pos_action.append(action)
next_state = r_pos_action[random.randint(0, len(r_pos_action) - 1)]
q[state, next_state] = r[state, next_state] + gamma * q[next_state].max()
state = next_state
print('Finally, the content of Q-table is:\n')
print(q)
# verification
for i in range(10):
print("\n{}-th verification:".format(i + 1))
state = random.randint(0, 5)
print('The robot is at {}'.format(state))
count = 0
while state != 5:
if count > 20:
print('fail')
break
# Choose the largest q_max
q_max = q[state].max()
q_max_action = []
for action in range(6):
if q[state, action] == q_max:
q_max_action.append(action)
next_state = q_max_action[random.randint(0, len(q_max_action) - 1)]
print("the robot goes to " + str(next_state) + '.')
state = next_state
count += 1
运行过程中,会输出最终Q-table中的数据,如下图所示:

接来下是部分验证阶段的输出,对照房间平面图可以发现,代理成功地通过了测试,如下图所示:
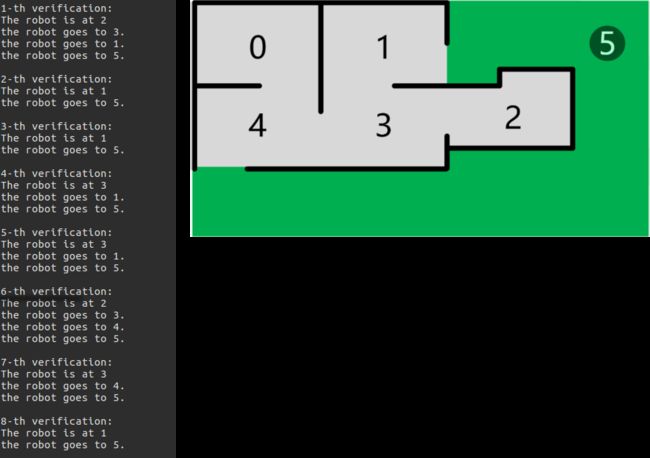
5. 小结
本笔记简要说明了如何进行Q-learning训练,并结合一个房间路径寻找的例子进行了完整分析。从算法描述可以看出,Q-learning方法没有利用model-based方法所依赖的状态转移概率矩阵 P P P,因此它是一种model-free的强化学习方法,其用到的查表思想简洁易懂,是初学者容易掌握的强化学习方法。
参考资料:
- DQN 从入门到放弃3 价值函数与Bellman方程
- Q-learning - Wikipedia
- 强化学习笔记(2)-从 Q-Learning 到 DQN
- 极简Qlearning教程(附Python源码)
- 理解Q-learning,一篇文章就够了
- A Painless Q-Learning Tutorial