哈夫曼树与编码(最优二叉树)
二叉树中有一种特别的树——哈夫曼树(最优二叉树),其通过某种规则(权值)来构造出——哈夫曼二叉树,在这个二叉树中,只有叶子节点才是有效的数据节点,其他的非叶子节点是为了构造出哈夫曼而引入的!
哈夫曼编码是一个通过哈夫曼树进行的一种编码,一般情况下,以字符:‘0’与‘1’表示。编码的实现过程很简单,只要实现哈夫曼树,通过遍历哈夫曼树,规定向左子树遍历一个节点编码为“0”,向右遍历一个节点编码为“1”,结束条件就是遍历到叶子节点!因为上面说过:哈夫曼树叶子节点才是有效数据节点!
下面就来一步一步实现这个过程:
前面已经说关键是构造一棵哈夫曼树,只要构造出了这棵哈夫曼树,编码就很简单,既然是二叉树那么我们首先就定义一个二叉树结构:
Class HFMT
{
public:
char date;//数据
int weight;//权值
int lchild ,rchild,parent=0;//左右孩子和双亲
char code[N]; // 字符的编码
};其中权值是我们最需要关心的,因为我们就是要通过权值来构造,但权值是怎么规定的呢?当然是根据实际情况来!
说到这里,我们为什么要引入哈夫曼树呢?
在哈夫曼问题中有一个参数是我们很关注的,那就是WPL(带权路径长度)也就是各叶节点的权值乘以他们的路径长度之和。正因为我们需要找到最短的WPL。
现在我们要考虑,我们要用怎样的存储结构来储存哈夫曼树呢?
我们可以设置一个HTnode类型的数组来保存哈夫曼树中的各个节点的信息,在通过每个节点中的lchild ,rchild,parent 信息来构造出树状结构。我们可以举一个简单的例子:
HFMT ht[9]={
{‘a’,0 ,5},
{‘b’,0,2},
{‘c’,0,9},
{‘d’,0,3},
{‘e’,0,6}
};
其中数组中每一个参数分别代表字符,是否有双亲和他们的权值,而且数组中每个元素都是一个哈夫曼树,我们现在的任务就是将这些元素“整合”起来,使它们联系起来构成一个哈夫曼树。初始时,数组每个元素都是没有联系的,我们的任务就是把它们通过lchild ,rchild,parent连接起来,形象上就是构成一棵二叉树。
我们先通过语言叙述的方法来构造一棵哈夫曼二叉树:
a 权值5
b权值2
c权值9
d权值3
e权值6
首先,取出权值最小的两个节点“整合”出一个新的节点,该节点的权值为最小两个节点权值之和。如下图:
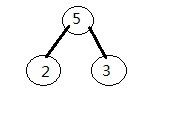
然后,将这个新的节点与剩下元素进行权值比较,依旧取最小的两个权值节点构造 新的节点,反复这个过程,直到取完所有元素,本例的哈夫曼树。如下图:
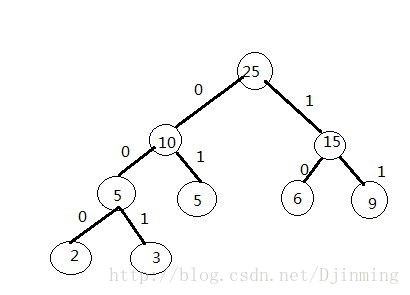
其中叶子节点(也就是2,3,5,6,9)是有效的数据节点!构造时节点的左右顺序并不影响哈曼树的构造,但会导致出现不同的编码,当然编码只要不出现前缀码就是正确的编码。
实现算法:
实现算法有很多种,关键是要理解它构造的原理。节点数组:HFMT ht[9]={{‘a’,0,5},{‘b’,0,2},{‘c’,0,9},{‘d’,0,3},{‘e’,0,6}};正如上文所说,首先,我们需要遍历这个数组,找到包含最小和次小的权值且无双亲的两个元素。然后,将权值求和充当新的节点的权值,该元素节点为ht[5],新的节点rchild lchild分别为权值最小的两个节点的序号1,3,让权值最小的两个节点的parent为新节点的序号5。最后,开始重新遍历。重复上述过程,直到数组填满,填满后的最后一个元素就是最终的哈夫曼树。并且通过上面的例子,我们知道构造一个哈夫曼树,如果有n个有效节点(叶节点),那么这个哈夫曼树共有2n-1个结点,如上面例子,有效数据个数有5个,但最终构造出的哈夫曼树有2*5-1=9个节点。
首先我们先定义一个HFMT的节点类:
#define N 10 // 带编码字符的个数,即树中叶结点的最大个数
#define M (2*N-1) // 树中总的结点数目
class HFMT
{
public:
int lchild, rchild, parent=0;
char data; // 待编码的字符
int weight; // 字符的权值
char code[N]; // 字符的编码
};然后通过一个初始化函数输入每一个节点的数据:
void init(HFMT ht[], int & n)//n是有效元素个数(叶子元素的个数)
{
cout << "input n =" << endl;
cin >> n;
cout << "input" << n << "character:" << endl;
for (int i = 1; i <= n; ++i) {
cin >> ht[i].data;//键入每个元素的字符
}
cout << "input" << n << "weight" << endl;
for (int i = 1; i <= n; ++i) {
cin >> ht[i].weight;//键入每个元素的权值
}
}下面我们可以实现算法来构造哈夫曼树,在此时我们最好先构造一个选择函数去挑选每轮权值最小和次小且无双亲的元素,来避免函数过于臃肿,选择函数如下代码避免了常见的BUG难免有些复杂:
void select(HFMT ht[], int k, int & s1, int & s2)//s1,s2用来保存挑选出来的元素的序号;k代表元素个数
{
int min1 = ht[k].weight;//min1,min2代表具有最小和次小的权值的元素
int min2 = ht[k].weight;
for (int i = 1; i <= k; i++)
{
if (ht[i].parent == 0)//找出具有最小权值的元素序号
{
if (ht[i].weight <= min1)
{
s1 = i;
min1 = ht[i].weight;
}
}
}
if (s1 == k)//如果序号为K的元素的权值最小,那么则找另一个序号最为次小权值的初始序号
{
for (int i = 1; i < k; i++)
{
if (i != s1&&ht[i].parent == 0)
{
min2 = ht[i].weight;
break;
}
}
}
for (int i = 1; i <= k; i++)//找出次小权值的元素序号
{
if (i != s1&&ht[i].parent == 0)
{
if (ht[i].weight <= min2)
{
s2 = i;
min2 = ht[i].weight;
}
}
}
}然后我们就可以调用函数来形成哈夫曼树,函数代码如下:
void huffmantree(HFMT ht[], int n)//n代表有效元素的序号,也就是叶子元素的序号
{
int m = 2 * n - 1;//m代表树中所有节点的个数
int s1, s2;
for (int i = n + 1; i <= m; ++i)
{
select(ht, i - 1, s1, s2);//选择,找出次小和最小
ht[s1].parent = i;
ht[s2].parent = i;//赋给双亲序号于孩子
ht[i].lchild = s1;
ht[i].rchild = s2;//赋给左右孩子于双亲
ht[i].weight = ht[s1].weight + ht[s2].weight;//赋权值于双亲
}
}我们成功的构造了一颗哈夫曼树,但是这还远远没有达到我们的预期,接下来就是遍历哈夫曼树求每一个字符的编码,代码如下:
void huffmancoding(HFMT ht[], int n)//n代表有效元素的个数
{
char *cd;
int f, start;
cd = new char [n];//创建字符数组空间储存编码
cd[n - 1] = '\0';//输入结束字符
for (int i = 1; i <= n; i++)//反序求字符的编码
{
start = n - 1;
int c = i;//保存i的值
for (i = c , f = ht[i].parent; f != 0; i = f, f = ht[f].parent)
//从下到上遍历找双亲
{
if (ht[f].lchild == i)
cd[--start] = '0';
else
cd[--start] = '1';
}
i = c;//将i恢复原来的值
strcpy(ht[i].code, &cd[start]);//将start以后的字段复制给strcpy
}
}