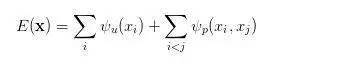FCN

 

大多数人接触"语义"都是在和文字相关的领域，或语音识别，期望机器能够识别你发出去的消息或简短的语音，然后给予你适当的反馈和回复。嗯，看到这里你应该已经猜到了，图像领域也是存在"语义"的。

今天是AI大热年，很多人都关注与机器人的语音交互，可是有没有想过，将来的机器人如果不能通过图像来识别主人，家里的物品、宠物，那该多没意思。说近一些，假如扫地机器人能够机智地绕开你丢在地上的臭袜子而扫走旁边的纸屑，一定能为你的生活解决不少麻烦。

没错，图像语义分割是AI领域中一个重要的分支，是机器视觉技术中关于图像理解的重要一环，是不是听上去即重要又牛X闪闪的。

近年的自动驾驶技术中，也需要用到这种技术。车载摄像头探查到图像，后台计算机可以自动将图像分割归类，以避让行人和车辆等障碍。

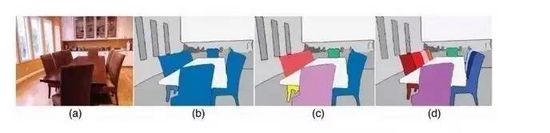
图像语义分割的意思就是机器自动分割并识别出图像中的内容，比如给出一个人骑摩托车的照片，机器判断后应当能够生成右侧图，红色标注为人，绿色是车（黑色表示back ground）。

所以图像分割对图像理解的意义，就好比读古书首先要断句一样。

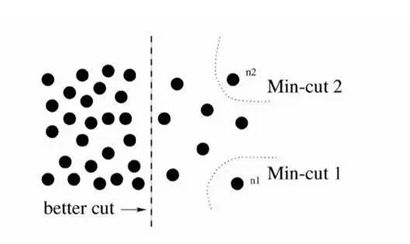
在Deeplearning技术快速发展之前，就已经有了很多做图像分割的技术，其中比较著名的是一种叫做"Normalized cut"的图划分方法，简称" N-cut "。

N-cut的计算有一些连接权重的公式，这里就不提了，它的思想主要是 通过像素和像素之间的关系权重来综合考虑 ，根据给出的阈值，将图像一分为二。

下图是将像素间的关系信息简单描述成为距离，根据距离差距来划分图像的示例：

在实际运用中，每运行一次N-cut，只能切割一次图片，为了分割出图像上的多个物体，需要多次运行，下图示例了对原图a进行7次N-cut后，每次分割出的结果。

但是可以很明显的看到这种简单粗暴的分割方式并不准确，趴在地上的运动员肢体在b图中分割出来，而他的手臂则在h图中被分割，显然是错误的。

N-cut技术的缺陷很明显，于是有了一种更新的优化方式，这种优化方式为了避免机器不能很好的分割类似上面例子中"衣服和肢体颜色反查太大导致分割错误"的情况，增加了人机交互，在分割过程中，需要人工干预参与完成。

这种需要人机交互的技术叫 Grab Cut 。

[敲黑板]~~ 注意，PS里就使用了这种技术。

这种技术其实是这样的，给定一张图片，然后人工在想要抠图（也就是我们说的分割）的区域画一个红框，然后机器会对略小于这个框的内容进行"主体计算"，嗯，这个"主体计算"是我起的名字，为了你们更好的理解背后复杂的设计和公式，因为机器会默认红框中部是用户期望得到的结果，所以将中部作为主体参考，然后剔除和主体差异较大的部分，留下结果。

此技术中，抠出来的部分叫"前景"，剔除的部分叫"背景"。

有时候还挺好用的，但是稍微复杂一点的时候问题就来了：比如要抠下面这个戴头盔的大兵，头盔颜色和背后岩石颜色很相近，结果机器就会把头盔部分剔除，同样脖子附近的山岩也被当做了前景而保留了进来。

此时又需要进行人工干预了，需要手动在图像上进行标注，画白色线表示是希望保留的前景，红色表示背景，指导辅助机器进行判断，再次运算后，得到了较好的期望结果。

虽然看上去Grab Cut给出的结果还不错，但缺点也很明显，首先，它同N-cut一样也只能做 二类语义分割 ，说人话就是一次只能分割一类，非黑即白，多个目标图像就要多次运算。其次，它需要人工干预，这个弱点在将来批量化处理和智能时代简直就是 死穴 。

OK，人类的智慧是无止境的， DeepLearning （深度学习）终于开始大行其道了。

深度学习是机器学习的一个分支，主要指 深度神经网络算法 ，深度神经网络比普通神经网络层次更多，能够更好地捕捉数据中的深层次关系，得到的模型较为准确，主要用来进行特征学习。

先别急着晕，我们先来看看神经网络是怎么工作的。

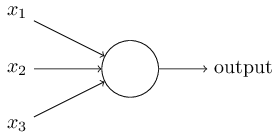
神经网络是模仿人的神经元而建立的人工神经元系统，多输入单输出，同时输出又作为下一个神经元的输入……（请自行脑补那张牙舞爪妖孽的神经元细胞~什么？没见过？文科生，拖出去~~）

下图表示的是一个单个神经元：

把这些单个神经元组织在一起，便形成了神经网络。下图便是一个三层神经网络结构：

上图中最左边的原始输入信息称之为 输入层 ，最右边的神经元称之为 输出层 （上图中输出层只有一个神经元），中间的叫 隐藏层 。

深度神经网络系统中的层数比较多，达到8-10层（普通神经网络的层数通常3-4层）。

在此前使用的图像识别算法中，主流的技术是 卷积神经网络算法 （Convolutional Neural Networks），简称 CNN 。 卷积神经网络就是一种深度神经网络 。

但是在2015年的CVPR上发表了一篇很牛X的论文（路人甲：请问CVPR是神马？答：CVPR可以简单理解为这个领域的最重量级的会议：国际计算机视觉与模式识别会议），提出了FCN即 全卷积神经网络 （Fully Convolutional Networks）。

为什么说这个FCN论文很牛叉呢？看起来只是多了一个字而已呀，有什么不得了的呢？

嗯，不得不说，真是" 差之毫厘，谬以千里 "啊。

我还是先来帮大家复习一下卷积。

我查了很多书，卷积有各种各样的公式，还有各种各样的推导算法，但是为了降低本文的难读指数，所以我直接跳到卷积的物理意义，不要太care那些公式，其实卷积的物理意义，就是" 加权叠加 "。

在对图像处理进行卷积时，根据卷积核的大小，输入和输出之间也会有规模上的差异。

来看一张动图（仅做示例）

上图左边5*5的方块视为图像输入，黄色移动的3*3以及里面的数字（*1/*0）是卷积核，该卷积核按照步长为1的顺序依次从原始输入的左上角一直移动计算叠加到右下角，卷积核一共移动9次。

九次的位置对应到右侧的3*3的相应格内，格中的数字便是卷积值，（此处是卷积核所覆盖的面积内元素相乘再累加的结果）。

9次移动计算完毕后，右侧3*3的新矩阵为此次卷积层的计算结果。

如果这么说还是不太好理解，没关系，我有更直观的办法^_^。

在实际计算过程中，输入是一张原始图片和滤波器filter（一组固定的权重，也就是上面我们说的 卷积核对应的实际意义 ）做内积后得到新的二维数据。

不同的滤波器filter会得到不同的输出数据，比如轮廓、颜色深浅，如果想提取图像的不同特征，需要用不同的滤波器filter提取想要的关于图像的特定信息。

上图为一个卷积层中的卷积处理过程，注意上下两次卷积核内容是不同的，所以得到两种处理结果。

等号右边的新的二维信息在CNN网络中，会作为下一个卷积层的输入，即在下一个卷积层计算时，右边的图像会作为输入的原始图像。

在CNN网络中，一共会进行5次卷积层计算。

路人甲：那最后会得到一个什么鬼？

沈MM：咳咳，在连续的5个卷积层计算后，紧跟这的是3个全连接层。

路人甲：什么是全连接层？

沈MM：全连接层，并不是一个二维图像，而是—— 一个 一维向量 。

路人甲已哭晕在厕所。

这三个一维向量的前两个向量长度是4096，最后一个向量长度是1000.

为什么是1000？

因为在CNN网络中，有1000个分类，最后的这个向量中的1000个元素表达的信息是：这张原始输入图片中的东西可能是这1000个分类中的物体的概率。

是的，一张图，算了半天，最后给出的是，这张图是个什么玩意的答案。

右侧绿色箭头指向的表示最后一个全连接层的向量中，表示各种物体的概率，上图被识别为一辆车。

好了，上面说的是卷积神经网络CNN的处理过程（相信我我已经很简化了）。

那么 全卷积 神经网络呢？

大家应该注意到，CNN的输入是图像，输出是一个结果，或者说是一个值，一个概率值。

FCN提出所追求的是，输入是一张图片是，输出也是一张图片， 学习像素到像素的映射 。

上图上半部分是CNN网络，下半部分是CN网络

那么" 全卷积 "又体现在哪里呢？

CNN网络中的后三层，都是一维的向量，计算方式不再采用卷积，所以丢失了二维信息，而FCN网络中，将这三层全部 转化为1*1的卷积核所对应等同向量长度的多通道卷积层 ，使后三层也全部采用卷积计算，整个模型中，全部都是卷积层，没有向量，所以称为"全卷积"。

FCN将第6层和7层分别从4096长度的向量转化为4096通道的卷积层，第8层则是21通道的卷积层。之所以第8层从1000缩减到21，是因为FCN使用的识别库是PASCAL VOC，在PASCAL VOC中有20种物体分类，另外一个background分类。（关于PASCAL VOC参见附录）

再多说一句，以下（甚至全文）所用到的分割图片中不同的颜色就表示不同的物体类别，一共有21种颜色：

CNN的识别是图像级的识别，也就是从图像到结果，而 FCN的识别是像素级的识别 ，对输入图像的每一个像素在输出上都有对应的判断标注，标明这个像素最可能是属于一个什么物体/类别。

在此处特别要指出的是，在实际的图像语义分割测试时，输入是一个H*W*3的三通道彩色图像，而输出是一个H*W的矩阵。

这就可以简单看做每一个像素所携带的信息是多维的，比如颜色，就分为3层，分别对应R、G、B三个值。（不知道什么是RGB的，鉴定为文科生，请迅速撤离，谢谢）

所以在进行卷积的时候，每一个通道都是要独立计算的，计算完之后再叠加，得到最终卷积层结果。

如果卷积核移动的步长为1，那么卷积是按照像素排列去挨个计算的，计算量可想而知会有多么庞大。但是在实际中，相邻的像素往往都是一类，按照像素依次计算就显得冗余，所以在卷积之后会对输出进行一次 池化（pooling）处理 。

那么什么又是 池化 呢？

来，我们再来看一张动图：

池化简单来说就是将输入图像切块，大部分时候我们选择不重叠的区域，假如池化的分割块大小为 h*h，分割的步长为 j，那么一般 h=j，就像上图，如果需要重叠，只需要 h>j 即可。

对完整图像切分，再取切分区域中所有值的 均值或最大值 作为代表该区域的新值，放入池化后的二维信息图中。得到的新图就是池化结果。

在CNN和FCN的网络模型中，每一个卷积层，都包含了[ 卷积 池化] 处理，这就是传说中的" 下采样 "，但这样处理之后的结果是：图像的像素信息变小了，每一层的像素信息都是前一层的1/2大小，到第五层的时候，图像大小为原始图像的 1/32 。

在CNN算法里，这并没有什么要紧的，因为CNN最终只输出一个结果："这个图上是个啥"，但是FCN不同，FCN是像素级别的识别，也就是输入有多少像素，输出就要多少像素，像素之间完全映射，并且在输出图像上有信息标注，指明每一个像素可能是什么物体/类别。

所以就必须对这1/32的图像进行 还原 。

这里用到个纯数学技术，叫" 反卷积 "，对第5层进行反卷积，可以将图像扩充至原来的大小（严格说是近似原始大小，一般会大一点，但是会裁剪掉，为什么会大的原理略复杂，这里先不提，以后写进阶版再放进来）。

——这个"反卷积"称为" 上采样 "。（和下采样对应）

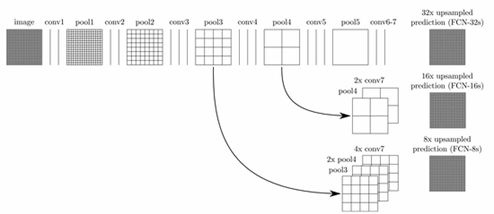
在技术上，我们可以对任一层卷积层做反卷积处理，得到最后的图像，比如用第三层(8s-8倍放大)，第四层(16s-16倍放大)，第五层(32s-32倍放大)得到的分割结果。

来看一张各层还原后的对比图，分别是：

通过对比可以很明显看到：在16倍还原和8倍还原时，能够看到更好的细节，32倍还原出来的图，在边缘分割和识别上，虽然大致的意思都出来了，但细节部分（边缘）真的很粗糙，甚至无法看出物体形状。

为什么会这样呢？

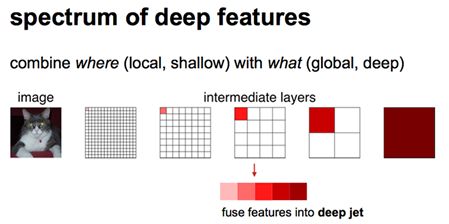
这里就涉及到一个 感受域 （receptive field）的概念。较浅的卷积层（靠前的）的感受域比较小，学习感知细节部分的能力强，较深的隐藏层(靠后的)，感受域相对较大，适合学习较为整体的、相对更宏观一些的特征。

所以在较深的卷积层上进行反卷积还原，自然会丢失很多细节特征。

于是我们会在反卷积步骤时，考虑采用一部分较浅层的反卷积信息辅助叠加，更好的优化分割结果的精度：

尽管FCN的提出是一条很牛叉的路，但还是无法避免有很多问题，比如，精度问题，对细节不敏感，以及像素与像素之间的关系，忽略空间的一致性等问题。

于是更牛的大牛就出现了。

有牛人提出一种新的卷积计算方式，开始称为"带hole"的卷积，也就是使用一种" 疏松的卷积核"来计算，以此来取代池化的处理。

上面已经讲过，池化操作能够减少计算量，同时也能防止计算结果过拟合，那么单纯取消池化操作又会使单层网络的感受域缩小，但如果使用"疏松的卷积核"来处理卷积，可以达到在不增加计算量的情况下增加感受域，弥补不进行池化处理后的精度问题。

括弧：这种带洞的卷积方式后来起了一个高雅的名字叫做："Dilated Convolutions"。

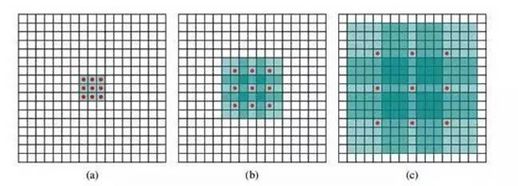
这种方式人为加大了卷积核内部元素之间的距离，可参考下图：

红点表示卷积核的元素，绿色表示感受域，黑线框表示输入图像。

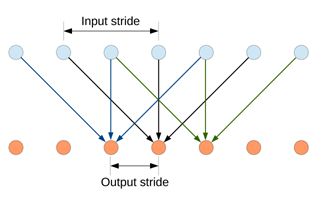
a为原始卷积核计算时覆盖的感受域，b为当卷积核覆盖的元素间距离增大的情况，不再在连续的空间内去做卷积，跳着做，当这个距离增加的越大时，单次计算覆盖的感受域面积越大。

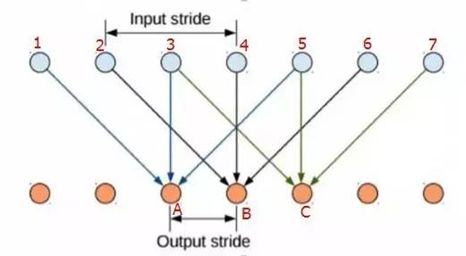
上图不太好理解的话再来看一张图：（个人觉得下面这个图非常好理解）

上层绿色点表示输入层像素点，下层黄色是输出层（单次计算时的层级关系），当卷积核元素间距为0时（相邻），123对应输出A，234对应输出B，345对应输出C，那么输出ABC三个元素结果的感受域只覆盖了12345这几个原始像素点。

如果采用稀疏的卷积核，假设间距为1（相当于卷积计算时跳一个像素再取值计算），如图示，那么结果A对应的输入是135，结果B对应的输入是246，结果C对应的输入是357，同样输出ABC三个结果，在原始图像上取的像素点的长度就多了。

这是水平X轴方向上的扩展，在Y轴上也会有同样的扩展，感受域在没有增加计算（相对于池化操作后）的情况下增大了，并且保留了足够多的细节信息，对图像还原后的精度有明显的提升。

看一下对比图：

第一列是原始图像，最后一列是手工标注的训练输入图像，第二列为FCN在1/8倍数下的还原，第三列则是采用了新的卷积算法的还原图像，可以很明显看到，第三列对细节的分割明显优于第二列FCN 8倍的图像。

刚才还提到了第二个问题，即像素与像素之间的逻辑关系的问题，毕竟前面再牛叉的算法也只是单纯的计算没有根据物理意义进行判断在输出的标注里这些结果是否合法（符合现实逻辑）。

很多以深度学习为框架的图像语义分割系统都使用了一种叫做" 条件随机场 "（ Conditional Random Field，简称 CRF ）的技术作为输出结果的优化后处理手段。其实类似技术种类较多，比如还有马尔科夫随机场(MRF)和高斯条件随机场(G-CRF)用的也比较多，但原理都较为类似。

简单来介绍一下"条件随机场"的概念。

FCN是像素到像素的影射，所以最终输出的图片上每一个像素都是标注了分类的，将这些分类简单地看成是不同的变量，每个像素都和其他像素之间建立一种连接，连接就是相互间的关系。

于是就会得到一个"完全图"：

上图是以4*6大小的图像像素阵列表示的简易版。

那么在全链接的 CRF 模型中，有一个对应的能量函数：

嗯，不要问我这个公式里各种符号是啥，我看不懂。但是我知道这个公式是干嘛滴：

其中等号右边第一个一元项，表示像素对应的语义类别，其类别可以由FCN或者其他语义分割模型的预测结果得到；而第二项为二元项，二元项可将像素之间的语义联系/关系考虑进去。

这么说太抽象，举个简单的例子，"天空"和"鸟"这样的像素在物理空间是相邻的概率，应该要比"天空"和"鱼"这样像素相邻的概率大，那么天空的边缘就更应该判断为鸟而不是鱼（从概率的角度）。

通过对这个能量函数优化求解，把明显不符合事实识别判断剔除，替换成合理的解释，得到对FCN的图像语义预测结果的优化，生成最终的语义分割结果。

优化后的对比图：

上图第二列是FCN网络8倍还原分割结果，第三列是将CRF植入FCN处理后的结果。

可以很明显的看到，第三列的物体识别无论是轮廓细节分割还是物体识别，都优于第二列，特别是第二行的沙发中有奇怪的红色东西的识别，在进行CRF优化之后，还原成了绿色的沙发。

OK，说了这么多，终于快要讲完了（好累）。

以上就是目前较为前沿的图像语义分割技术。

目前的这种机器学习方式还属于 监督性学习 ，牛叉闪闪的科学家们还是希望将来可以实现 半监督 或 弱监督式 学习，这样更类似人类的学习认知方式。

在这条道路上，还有很多有趣的东西，比如 示例级别（instance level）的图像语义分割 问题也同样热门。

该类问题不仅需要对不同语义物体进行图像分割，同时还要求对同一语义的不同个体进行分割（例如需要对图中出现的九把椅子的像素用不同颜色分别标示出来）。

另外，在目前的计算技术水平下（硬件软件），使用FCN训练建模的时间大约需要三周，这也说明在这个领域里还有很多值得探索和需要解决的问题。

对此有兴趣的同学们自己去继续研究吧，哈哈。

曾有一个业界大牛说过这样一段话，送给大家：

"华人在计算机视觉领域的研究水平越来越高，这是非常振奋人心的事。我们中国错过了工业革命，错过了电气革命，信息革命也只是跟随状态。但人工智能的革命，我们跟世界上的领先国家是并肩往前跑的。能身处这个时代浪潮之中，做一番伟大的事业，经常激动的夜不能寐。"

AI的浪潮即将席卷而来，你，准备好了么？

 

 

 

-----------------------------------分割线--------------------------------------------

 

 

 

 

背景

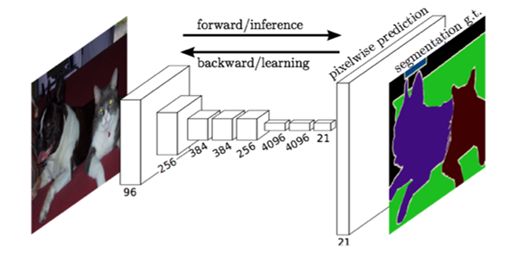
CNN能够对图片进行分类，可是怎么样才能识别图片中特定部分的物体，在2015年之前还是一个世界难题。神经网络大神Jonathan Long发表了《Fully Convolutional Networks for Semantic Segmentation》在图像语义分割挖了一个坑，于是无穷无尽的人往坑里面跳。

全卷积网络 Fully Convolutional Networks

CNN 与 FCN

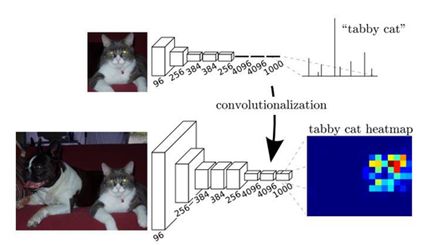
通常CNN网络在卷积层之后会接上若干个全连接层, 将卷积层产生的特征图(feature map)映射成一个固定长度的特征向量。以AlexNet为代表的经典CNN结构适合于图像级的分类和回归任务，因为它们最后都期望得到整个输入图像的一个数值描述（概率），比如AlexNet的ImageNet模型输出一个1000维的向量表示输入图像属于每一类的概率(softmax归一化)。

栗子：下图中的猫, 输入AlexNet, 得到一个长为1000的输出向量, 表示输入图像属于每一类的概率, 其中在"tabby cat"这一类统计概率最高。

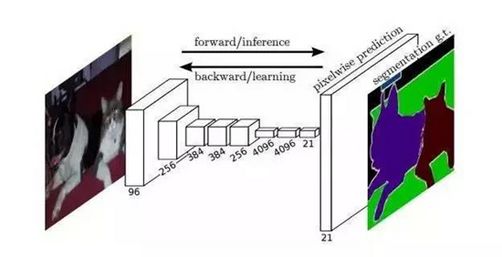
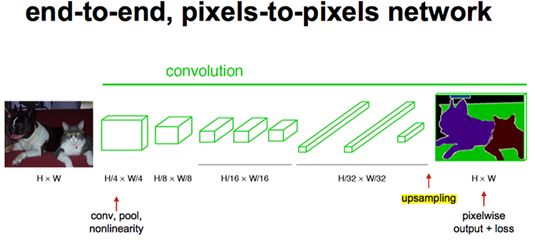
FCN对图像进行像素级的分类，从而解决了语义级别的图像分割（semantic segmentation）问题。与经典的CNN在卷积层之后使用全连接层得到固定长度的特征向量进行分类（全联接层＋softmax输出）不同，FCN可以接受任意尺寸的输入图像，采用反卷积层对最后一个卷积层的feature map进行上采样, 使它恢复到输入图像相同的尺寸，从而可以对每个像素都产生了一个预测, 同时保留了原始输入图像中的空间信息, 最后在上采样的特征图上进行逐像素分类。

最后逐个像素计算softmax分类的损失, 相当于每一个像素对应一个训练样本。下图是Longjon用于语义分割所采用的全卷积网络(FCN)的结构示意图：

简单的来说，FCN与CNN的区域在把于CNN最后的全连接层换成卷积层，输出的是一张已经Label好的图片。

其实，CNN的强大之处在于它的多层结构能自动学习特征，并且可以学习到多个层次的特征：较浅的卷积层感知域较小，学习到一些局部区域的特征；较深的卷积层具有较大的感知域，能够学习到更加抽象一些的特征。这些抽象特征对物体的大小、位置和方向等敏感性更低，从而有助于识别性能的提高。下图CNN分类网络的示意图：

这些抽象的特征对分类很有帮助，可以很好地判断出一幅图像中包含什么类别的物体，但是因为丢失了一些物体的细节，不能很好地给出物体的具体轮廓、指出每个像素具体属于哪个物体，因此做到精确的分割就很有难度。

传统的基于CNN的分割方法：为了对一个像素分类，使用该像素周围的一个图像块作为CNN的输入用于训练和预测。这种方法有几个缺点：一是存储开销很大。例如对每个像素使用的图像块的大小为15x15，然后不断滑动窗口，每次滑动的窗口给CNN进行判别分类，因此则所需的存储空间根据滑动窗口的次数和大小急剧上升。二是计算效率低下。相邻的像素块基本上是重复的，针对每个像素块逐个计算卷积，这种计算也有很大程度上的重复。三是像素块大小的限制了感知区域的大小。通常像素块的大小比整幅图像的大小小很多，只能提取一些局部的特征，从而导致分类的性能受到限制。

而全卷积网络(FCN)则是从抽象的特征中恢复出每个像素所属的类别。即从图像级别的分类进一步延伸到像素级别的分类。

 

全连接层 -> 卷积层

全连接层和卷积层之间唯一的不同就是卷积层中的神经元只与输入数据中的一个局部区域连接，并且在卷积列中的神经元共享参数。然而在两类层中，神经元都是计算点积，所以它们的函数形式是一样的。因此，将此两者相互转化是可能的：

• 对于任一个卷积层，都存在一个能实现和它一样的前向传播函数的全连接层。权重矩阵是一个巨大的矩阵，除了某些特定块，其余部分都是零。而在其中大部分块中，元素都是相等的。
• 相反，任何全连接层都可以被转化为卷积层。比如，一个 K=4096 的全连接层，输入数据体的尺寸是 7∗7∗512，这个全连接层可以被等效地看做一个 F=7,P=0,S=1,K=4096 的卷积层。换句话说，就是将滤波器的尺寸设置为和输入数据体的尺寸一致了。因为只有一个单独的深度列覆盖并滑过输入数据体，所以输出将变成 1∗1∗4096，这个结果就和使用初始的那个全连接层一样了。

全连接层转化为卷积层：在两种变换中，将全连接层转化为卷积层在实际运用中更加有用。假设一个卷积神经网络的输入是 224x224x3 的图像，一系列的卷积层和下采样层将图像数据变为尺寸为 7x7x512 的激活数据体。AlexNet使用了两个尺寸为4096的全连接层，最后一个有1000个神经元的全连接层用于计算分类评分。我们可以将这3个全连接层中的任意一个转化为卷积层：

• 针对第一个连接区域是[7x7x512]的全连接层，令其滤波器尺寸为F=7，这样输出数据体就为[1x1x4096]了。
• 针对第二个全连接层，令其滤波器尺寸为F=1，这样输出数据体为[1x1x4096]。
• 对最后一个全连接层也做类似的，令其F=1，最终输出为[1x1x1000]

实际操作中，每次这样的变换都需要把全连接层的权重W重塑成卷积层的滤波器。那么这样的转化有什么作用呢？它在下面的情况下可以更高效：让卷积网络在一张更大的输入图片上滑动，得到多个输出，这样的转化可以让我们在单个向前传播的过程中完成上述的操作。

举个栗子：如果我们想让224×224尺寸的浮窗，以步长为32在384×384的图片上滑动，把每个经停的位置都带入卷积网络，最后得到6×6个位置的类别得分。上述的把全连接层转换成卷积层的做法会更简便。如果224×224的输入图片经过卷积层和下采样层之后得到了[7x7x512]的数组，那么，384×384的大图片直接经过同样的卷积层和下采样层之后会得到[12x12x512]的数组。然后再经过上面由3个全连接层转化得到的3个卷积层，最终得到[6x6x1000]的输出((12 – 7)/1 + 1 = 6)。这个结果正是浮窗在原图经停的6×6个位置的得分！

面对384×384的图像，让（含全连接层）的初始卷积神经网络以32像素的步长独立对图像中的224×224块进行多次评价，其效果和使用把全连接层变换为卷积层后的卷积神经网络进行一次前向传播是一样的。

Evaluating the original ConvNet (with FC layers) independently across 224x224 crops of the 384x384 image in strides of 32 pixels gives an identical result to forwarding the converted ConvNet one time.

如下图所示，FCN将传统CNN中的全连接层转化成卷积层，对应CNN网络FCN把最后三层全连接层转换成为三层卷积层。在传统的CNN结构中，前5层是卷积层，第6层和第7层分别是一个长度为4096的一维向量，第8层是长度为1000的一维向量，分别对应1000个不同类别的概率。FCN将这3层表示为卷积层，卷积核的大小 (通道数，宽，高) 分别为 (4096,1,1)、(4096,1,1)、(1000,1,1)。看上去数字上并没有什么差别，但是卷积跟全连接是不一样的概念和计算过程，使用的是之前CNN已经训练好的权值和偏置，但是不一样的在于权值和偏置是有自己的范围，属于自己的一个卷积核。因此FCN网络中所有的层都是卷积层，故称为全卷积网络。

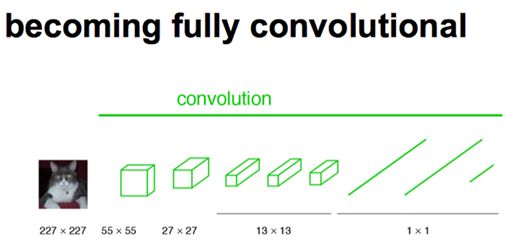
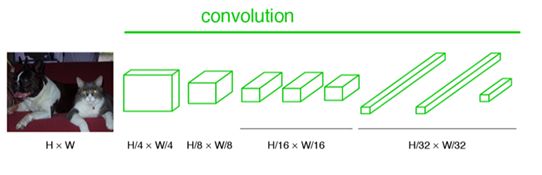
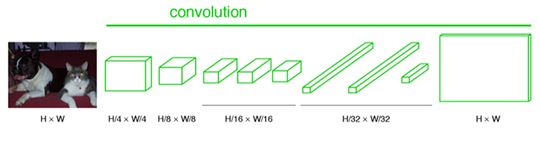
下图是一个全卷积层，与上图不一样的是图像对应的大小下标，CNN中输入的图像大小是同意固定resize成 227x227 大小的图像，第一层pooling后为55x55，第二层pooling后图像大小为27x27，第五层pooling后的图像大小为13*13。而FCN输入的图像是H*W大小，第一层pooling后变为原图大小的1/4，第二层变为原图大小的1/8，第五层变为原图大小的1/16，第八层变为原图大小的1/32（勘误：其实真正代码当中第一层是1/2，以此类推）。

经过多次卷积和pooling以后，得到的图像越来越小，分辨率越来越低。其中图像到 H/32∗W/32 的时候图片是最小的一层时，所产生图叫做heatmap热图，热图就是我们最重要的高维特征图，得到高维特征的heatmap之后就是最重要的一步也是最后的一步对原图像进行upsampling，把图像进行放大、放大、放大，到原图像的大小。

最后的输出是1000张heatmap经过upsampling变为原图大小的图片，为了对每个像素进行分类预测label成最后已经进行语义分割的图像，这里有一个小trick，就是最后通过逐个像素地求其在1000张图像该像素位置的最大数值描述（概率）作为该像素的分类。因此产生了一张已经分类好的图片，如下图右侧有狗狗和猫猫的图。

 

upsampling

相较于使用被转化前的原始卷积神经网络对所有36个位置进行迭代计算，使用转化后的卷积神经网络进行一次前向传播计算要高效得多，因为36次计算都在共享计算资源。这一技巧在实践中经常使用，一次来获得更好的结果。比如，通常将一张图像尺寸变得更大，然后使用变换后的卷积神经网络来对空间上很多不同位置进行评价得到分类评分，然后在求这些分值的平均值。

最后，如果我们想用步长小于32的浮窗怎么办？用多次的向前传播就可以解决。比如我们想用步长为16的浮窗。那么先使用原图在转化后的卷积网络执行向前传播，然后分别沿宽度，沿高度，最后同时沿宽度和高度，把原始图片分别平移16个像素，然后把这些平移之后的图分别带入卷积网络。

如下图所示，当图片在网络中经过处理后变成越小的图片，其特征也越明显，就像图像中颜色所示，当然啦，最后一层的图片不再是一个1个像素的图片，而是原图像 H/32xW/32 大小的图，这里为了简化而画成一个像素而已。

 

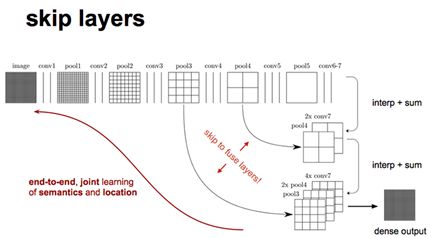
如下图所示，对原图像进行卷积conv1、pool1后原图像缩小为1/2；之后对图像进行第二次conv2、pool2后图像缩小为1/4；接着继续对图像进行第三次卷积操作conv3、pool3缩小为原图像的1/8，此时保留pool3的featureMap；接着继续对图像进行第四次卷积操作conv4、pool4，缩小为原图像的1/16，保留pool4的featureMap；最后对图像进行第五次卷积操作conv5、pool5，缩小为原图像的1/32，然后把原来CNN操作中的全连接变成卷积操作conv6、conv7，图像的featureMap数量改变但是图像大小依然为原图的1/32，此时图像不再叫featureMap而是叫heatMap。

现在我们有1/32尺寸的heatMap，1/16尺寸的featureMap和1/8尺寸的featureMap，1/32尺寸的heatMap进行upsampling操作之后，因为这样的操作还原的图片仅仅是conv5中的卷积核中的特征，限于精度问题不能够很好地还原图像当中的特征，因此在这里向前迭代。把conv4中的卷积核对上一次upsampling之后的图进行反卷积补充细节（相当于一个差值过程），最后把conv3中的卷积核对刚才upsampling之后的图像进行再次反卷积补充细节，最后就完成了整个图像的还原。

 

缺点

在这里我们要注意的是FCN的缺点：

1. 是得到的结果还是不够精细。进行8倍上采样虽然比32倍的效果好了很多，但是上采样的结果还是比较模糊和平滑，对图像中的细节不敏感。
2. 是对各个像素进行分类，没有充分考虑像素与像素之间的关系。忽略了在通常的基于像素分类的分割方法中使用的空间规整（spatial regularization）步骤，缺乏空间一致性。

    

    

    

   -----------------------------------分割线--------------------------------------------

    

    

    

    

   从图像分类到图像分割

   卷积神经网络（CNN）自2012年以来，在图像分类和图像检测等方面取得了巨大的成就和广泛的应用。

   CNN的强大之处在于它的多层结构能自动学习特征，并且可以学习到多个层次的特征：较浅的卷积层感知域较小，学习到一些局部区域的特征；较深的卷积层具有较大的感知域，能够学习到更加抽象一些的特征。这些抽象特征对物体的大小、位置和方向等敏感性更低，从而有助于识别性能的提高。

   这些抽象的特征对分类很有帮助，可以很好地判断出一幅图像中包含什么类别的物体，但是因为丢失了一些物体的细节，不能很好地给出物体的具体轮廓、指出每个像素具体属于哪个物体，因此做到精确的分割就很有难度。

   传统的基于CNN的分割方法的做法通常是：为了对一个像素分类，使用该像素周围的一个图像块作为CNN的输入用于训练和预测。这种方法有几个缺点：一是存储开销很大。例如对每个像素使用的图像块的大小为15x15，则所需的存储空间为原来图像的225倍。二是计算效率低下。相邻的像素块基本上是重复的，针对每个像素块逐个计算卷积，这种计算也有很大程度上的重复。三是像素块大小的限制了感知区域的大小。通常像素块的大小比整幅图像的大小小很多，只能提取一些局部的特征，从而导致分类的性能受到限制。

   针对这个问题, UC Berkeley的Jonathan Long等人提出了Fully Convolutional Networks (FCN)[1]用于图像的分割。该网络试图从抽象的特征中恢复出每个像素所属的类别。即从图像级别的分类进一步延伸到像素级别的分类。

    

   FCN的原理

   FCN将传统CNN中的全连接层转化成一个个的卷积层。如下图所示，在传统的CNN结构中，前5层是卷积层，第6层和第7层分别是一个长度为4096的一维向量，第8层是长度为1000的一维向量，分别对应1000个类别的概率。FCN将这3层表示为卷积层，卷积核的大小(通道数，宽，高)分别为（4096,1,1）、（4096,1,1）、（1000,1,1）。所有的层都是卷积层，故称为全卷积网络。 
   

   可以发现，经过多次卷积（还有pooling）以后，得到的图像越来越小,分辨率越来越低（粗略的图像），那么FCN是如何得到图像中每一个像素的类别的呢？为了从这个分辨率低的粗略图像恢复到原图的分辨率，FCN使用了上采样。例如经过5次卷积(和pooling)以后，图像的分辨率依次缩小了2，4，8，16，32倍。对于最后一层的输出图像，需要进行32倍的上采样，以得到原图一样的大小。

   这个上采样是通过反卷积（deconvolution）实现的。对第5层的输出（32倍放大）反卷积到原图大小，得到的结果还是不够精确，一些细节无法恢复。于是Jonathan将第4层的输出和第3层的输出也依次反卷积，分别需要16倍和8倍上采样，结果就精细一些了。下图是这个卷积和反卷积上采样的过程： 
   

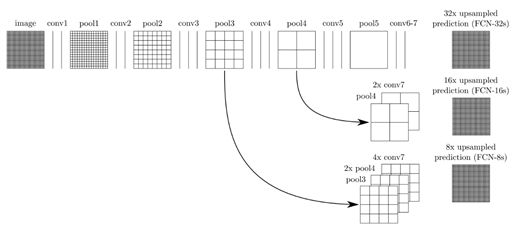
   下图是32倍，16倍和8倍上采样得到的结果的对比，可以看到它们得到的结果越来越精确： 
   

    

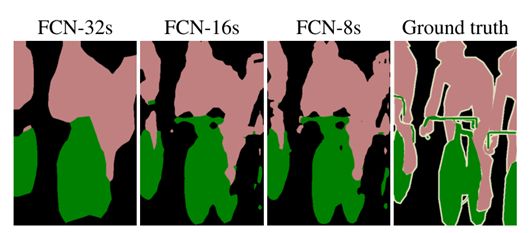
   FCN的优点和不足

   与传统用CNN进行图像分割的方法相比，FCN有两大明显的优点：一是可以接受任意大小的输入图像，而不用要求所有的训练图像和测试图像具有同样的尺寸。二是更加高效，因为避免了由于使用像素块而带来的重复存储和计算卷积的问题。

   同时FCN的缺点也比较明显：一是得到的结果还是不够精细。进行8倍上采样虽然比32倍的效果好了很多，但是上采样的结果还是比较模糊和平滑，对图像中的细节不敏感。二是对各个像素进行分类，没有充分考虑像素与像素之间的关系，忽略了在通常的基于像素分类的分割方法中使用的空间规整（spatial regularization）步骤，缺乏空间一致性。

    

   FCN的扩展

   虽然FCN不够完美，但是其全新的思路开辟了一个新的图像分割方向，对这个领域的影响是十分巨大的，从2015年3月在arxiv和6月在CVPR会议上发表到写下这篇博客的时候一年的时间，该文章已被引用高达400次。

   在FCN的基础上，UCLA DeepLab的Liang-Chieh Chen[2]等在得到像素分类结果后使用了全连接的条件随机场（fully connected conditional random fields），考虑图像中的空间信息，得到更加精细并且具有空间一致性的结果。

   Liang-Chieh的这篇文章有两大特点，一是忽略下采样过程，转而使用稀疏的卷积核以增加感知范围。如下图所示： 
   

   二是使用了Fully Connected CRF。CRF的能量函数中包括数据项和平滑项两部分，数据项与各个像素属于各类别的概率有关，平滑项控制像素与像素间类别的一致性。传统的CRF的平滑项只考虑相邻像素类别的关联性，而Fully Connected CRF将图像中任意两个像素之间的类别关联性都考虑进来。

   下图是CNN与Fully Connected CRF结合的示意图。 
   

   实际上，CRF或者Fully Connected CRF是对CNN或者FCN输出的一种后处理技术。像素分类和空间规整这两步是分别进行的。Shuai Zheng[3]等人将Fully Connected CRF表示成回流神经网络的结构(recurrent neuron network，RNN)，将CNN与这个RNN放到一个统一的框架中，可以一步到位地对两者同时进行训练。将图像分割中的三个步骤：特征提取、分类器预测和空间规整全部自动化处理，通过学习获得，得到的结果比FCN-8s和DeepLab的方法的效果好了许多。如下图结果： 
   

   CNN、FCN与Fully Connected CRF的结合及统一的自动训练具有很不错的应用价值，已有很多的研究对这几篇文章进行跟进（[2]和[3]的引用都已过百）。例如，帝国理工的Konstantinos Kamnitsas，Daniel Rueckert等人在这几篇文章的基础上，提出了三维的多尺度CNN和全连接CRF结合的方法，称为DeepMedic, 用于脑肿瘤的分割，最近（4月4号）刚发表于arXiv。

   参考文献 
   1，Long, Jonathan, Evan Shelhamer, and Trevor Darrell. "Fully convolutional networks for semantic segmentation." Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2015. 
   2，Chen, Liang-Chieh, et al. "Semantic image segmentation with deep convolutional nets and fully connected crfs." arXiv preprint arXiv:1412.7062 (2014). 
   3，Zheng, Shuai, et al. "Conditional random fields as recurrent neural networks." Proceedings of the IEEE International Conference on Computer Vision. 2015. 
   4，Kamnitsas, Konstantinos, et al. "Efficient Multi-Scale 3D CNN with Fully Connected CRF for Accurate Brain Lesion Segmentation." arXiv preprint arXiv:1603.05959 (2016).