从CPU cache一致性的角度看Linux spinlock的不可伸缩性(non-scalable)

凌晨一点半的深圳雨夜：

豪雨当夜惊起有人赏，笑叹落花无声空飘零。
喜欢这种豪雨，让人兴奋。惊起作文以呜呼之感叹！

---

引用上一篇文章：
优化多核CPU的TCP新建连接性能–重排spinlock：https://blog.csdn.net/dog250/article/details/80575731
在这篇文章中，我将一个spinlock拆解成了per cpu的，然而并没有提及spinlock本身的性能和可伸缩性(scalable)，那么本文就来说一下。

---

一点说明

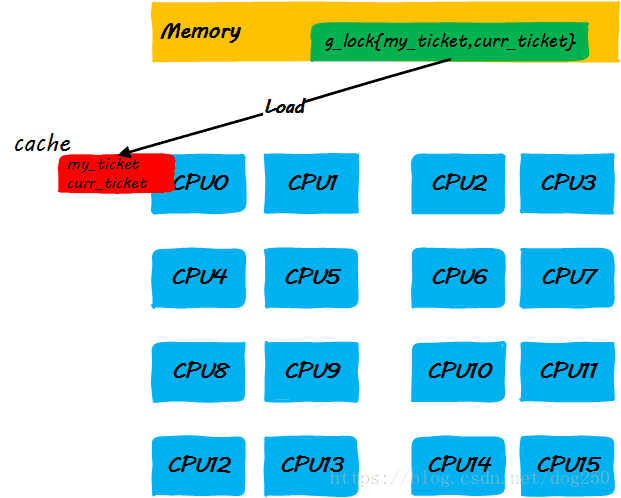
正文开始之前，先给出本文讨论的各个场景基于的CPU布局图，本文中我们将描述很多的场景实验，因为是分析原理，我将其定义为思想实验，假设我们思想实验的系统拥有16核CPU，其中每一个CPU封装有2个物理核，每一个物理核有两个有独立cache的核心，其布局如下：

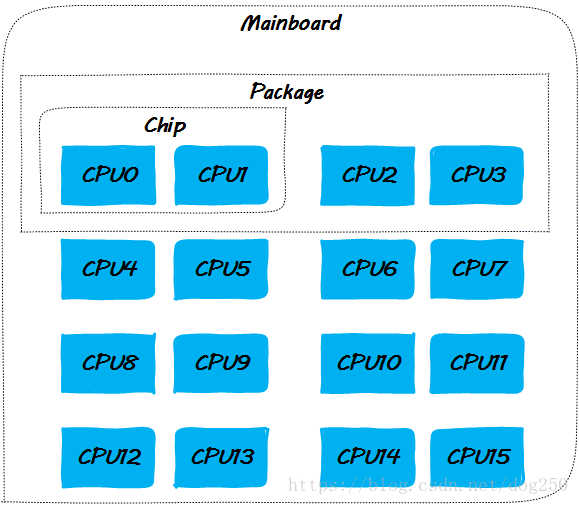
由于实现的可扩展性的原因，当前的大多数平台在实现CPU cache一致性协议时有两个选择，一个是snoopy，一个是点对点unicast。

• snoopy方式
  这意味着cache一致性消息通过总线广播，于是就要侦听总线以在某个时机获得控制权。这种方式及其不易扩展，在CPU数目达到一定量时，总线的争抢会很严重。
  参考以太网的CSMA/CD协议，会得出一样的结论，正如CSMA/CD的基于总线的以太网由于其不可扩展性进化到了交换式以太网一样，CPU间的cache一致性协议的点对点unicast实现方式最终替代了snoopy(小规模本地cache一致性依然会采用snoopy的方式)。总而言之，是总线带宽限制了snoopy想大规模SMP发展。
• 点对点unicast方式
  既然snoopy需要严格的总线仲裁，采用点对点的方式进行cache一致性的消息路由就成了一个可选的应对措施，但是对于多个目的地的消息的发送方而言，one by one的按序in turn方式发送就成了唯一的选择，正是这种处理方式成了点对点unicast方式的另一个不可扩展性根源。
  但这种不可扩展性是针对更上层而言，在cache一致性协议的实现上，它克服了总线仲裁带来的本层的不可扩展性。业界很多的场景都遵循了类似的总线–>点对点的发展轨迹，除了以太网之外，还有PCI到PCIe的进化。无论哪种实现方式，其过程都体现了采用被动的NAK仲裁向主动的消息路由方向的进化之路似乎是一条放之四海而皆准的康庄大道。

理解这些，特别是理解点对点unicast方式的one by one处理时延会随着CPU核数的增加而线性增加为后面的内容埋下了伏笔。

---

在Linux内核中，先后有过新旧两种版本的自旋锁被大规模使用，一个是willd spinlock，另一个则是当前内核默认使用的ticket spinlock，下面的章节会简而述之。

好了，正文开始！

---

wild spinlock

这种自旋锁非常简单，简而言之就是一个整数：

typedef struct {
    volatile unsigned int lock;
} spinlock_t;

然后其加锁和解锁过程为：

void spin_lock(spinlock_t *lock)
{
    while (lock->lock == 1)
        ; // 自旋等待
}
void spin_unlock(spinlock_t *lock)
{
    lock->lock = 0;
}

然而在这种简单的背后却掩盖着一个血雨腥风的战场，我们看一下why。

根据上面的CPU布局图，我们可以了解到CPU之间的亲密关系是不同的，特定CPU的cache line更新同步到不同CPU的cache line的时间也不同，这就意味着等待自旋锁的CPU中哪个CPU先感知到lock->lock的变化，哪个就能优先获得锁。

这将大大有损等锁者之间的公平性。这就好比一群人不排队上火车，体格好的总是优先登车一样。

为了解决这个公平性问题，ticket spinlock登场了。

ticket spinlock登场

ticket spinlock在设计上增加了一个等锁期间单调递增的ticket字段(当然，在实现上如何体现这个ticket就是trick了)，确保了先到者先获得锁，从而保证了公平性。

---

Linux ticket spinlock的实现和执行过程

我先给出Linux ticket spinlock的伪代码实现，为了讨论简单，以下的代码中所有的自加(i++)操作均为原子操作，避免锁中锁。

• 定义spinlock

struct spinlock_t {
    // 上锁者自己的排队号
    int my_ticket;
    // 当前叫号
    int curr_ticket;
}

非常简单，一个标准的排队装置，类似银行叫号系统，每个办理业务的取一个号，然后按照号码的大小依次串行被服务。

• spin_lock上锁

void spin_lock(spinlock_t *lock)
{
    int my_ticket;
    // 顺位拿到自己的ticket号码；
    my_ticket = lock->my_ticket++;
    while (my_ticket != lock->curr_ticket)
        ; // 自旋等待！
}

• spin_unlock解锁

void spin_unlock(spinlock_t *lock)
{
    // 呼叫下一位！
    lock->curr_ticket++;
}

以上基本就是Linux ticket spinlock实现的全部了，没什么复杂的，没什么大不了的。如果说仅仅是为了读懂代码，确实没有什么大不了的，然而深究起来却可以发现它的不妙。

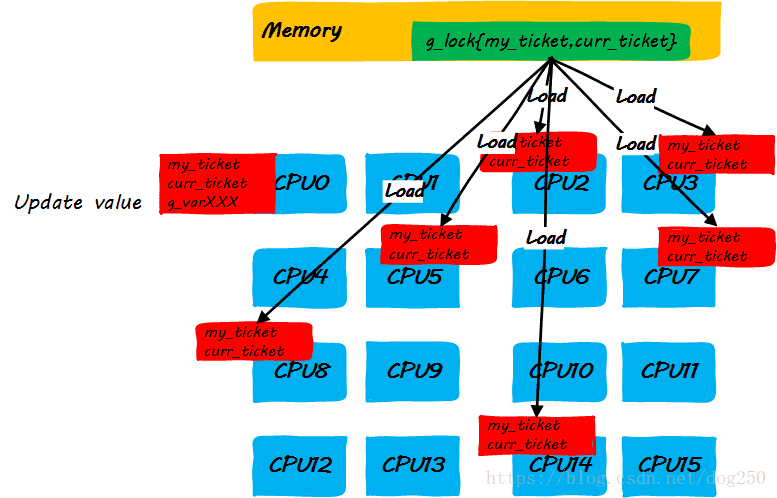
以下我就从cache的角度来分析一下这个自旋锁的执行过程，以下面的代码片段为例：

void demo()
{
    spin_lock(&g_lock);
    g_var1 ++;
    g_var2 --;
    g_var3 = g_var1 + g_var2;
    spin_unlock(&g_lock)
}

依然是按步骤来。好了，开始我们的步骤。

• step 1：CPU0申请锁，获取本地ticket到申请者的CPU cache
  
• step 2：执行锁定区域指令的同时，其它CPU企图获取锁而自旋
  
• step 3：CPU0释放锁
  

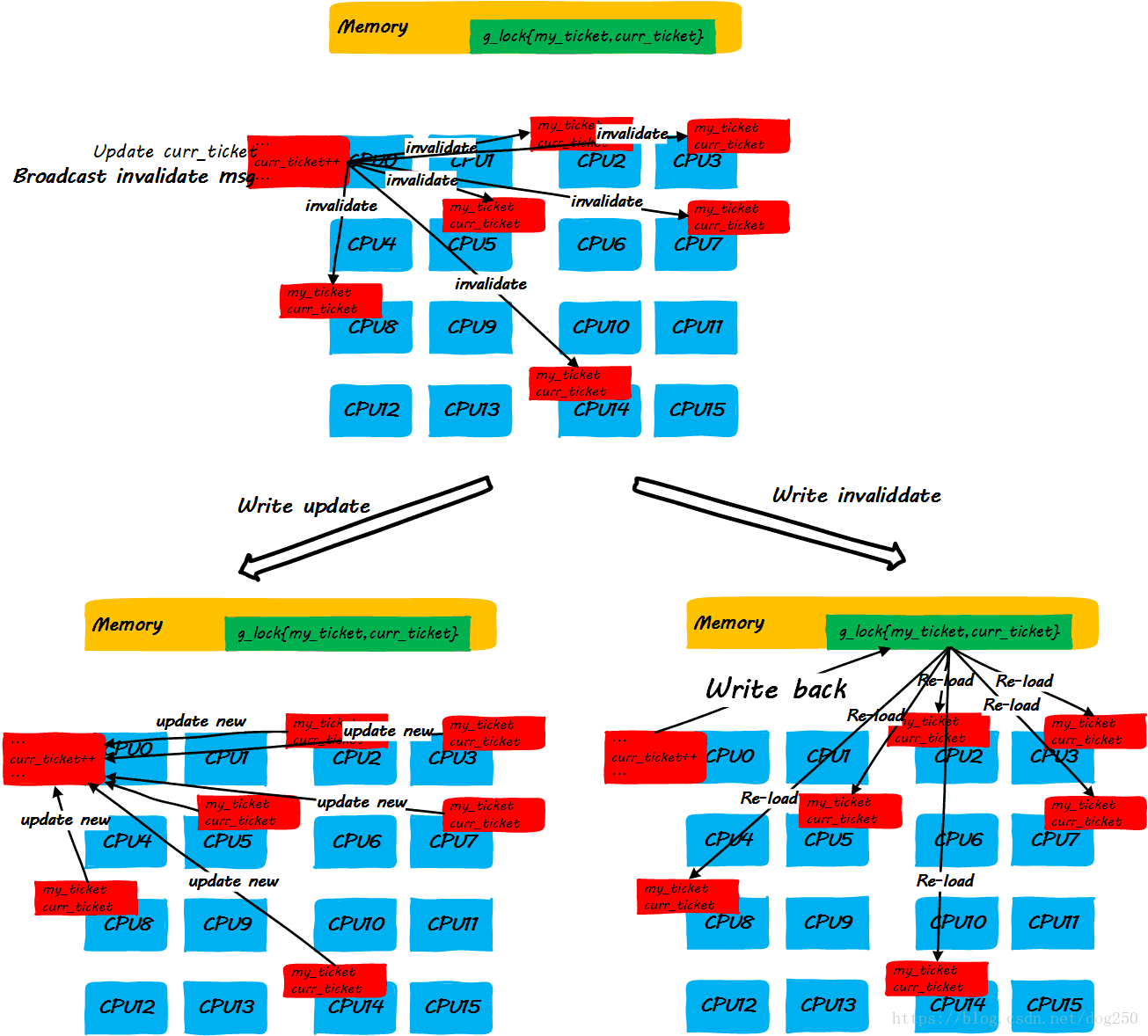
我们发现，上述的step3中的步骤有点太复杂了。当前的大多数平台倾向于用点对点unicast的方式来更新cache line(因为broadcast方式对总线带宽有要求，随着CPU核数的增加，实现复杂度会增加，这是另一种不可伸缩！)，因此step3中更新每一个CPU cache line是一个one by one的过程，如果是write invalidate方式，就更会多出超级多的访存指令，这些对于理解Linux ticket spinlock的不可伸缩性至关重要！

很显然，随着CPU核数的增加，随着spinlock申请者的增加，step3中动作的执行时间会线性增加，最终，当spinlock的申请者达到一定数量时，多核CPU非但没有提高性能，反而由于cache line更新的时间过久，反过来损害性能。

注意，wild spinlock同样存在这个问题，wild spinlock背后的cache一致性过程和ticket spinlock完全一致，只是ticket spinlock严格限定了谁将下一个获得锁而wild spinlock并不能。

---

我们已经定性地描述了Linux ticket spinlock的当前实现会有什么问题，为了定量地衡量这种实现会带来哪些具体的后果，我需要简单说一下Linux ticket spinlock(此后简称Linux spinlock)经典的Markov chain模型，请看下节。

Linux spinlock的马尔科夫链模型

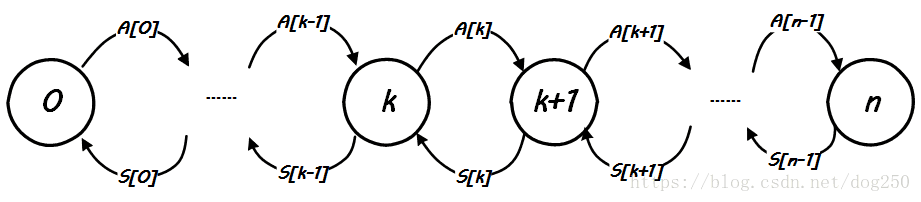
为了阐释Linux spinlock的具体性能表现和带来的结果，必然需要建立一个模型，本节我就说一下Linux spinlock的Markov chain模型，该模型结合排队论可以精确描述和预测Linux spinlock的行为。

先看一下图示：

解释一下：

这是一个Markov chain，其中一共有 0 0 , 1 1 ,… n n 一共 n+1 n + 1 个状态，每一个状态 k k ，表示系统中有 k k 个CPU正在自旋等待锁， A[k] A [ k ] 表示状态 k k 转换到状态 k+1 k + 1 的速率，也就是相当于请求锁的速率，而 S[k] S [ k ] 则表示状态 k+1 k + 1 转换到状态 k k 的速率，也就是相当于释放锁的速率。

简化起见，我们忽略掉spinlock到达的细节，即设在单一CPU核心上spinlock的请求达平均间隔为 Tarrive T a r r i v e (事实上应该是指数分布)，那么单一CPU核心的spinlock请求到达的速率就是 1Tarrive 1 T a r r i v e (事实上应该是泊松分布)，由于我们的思想实验基于多核CPU平台，因此总体上的spinlock请求到达的速率和空闲CPU个数成正比。假设当前的 n n 核CPU系统上已经有 k k 个CPU在自旋等锁了，那么 n−k n − k 个CPU上spinlock的到达速率为 n−kTarrive n − k T a r r i v e ，因此，上图中的 A[k] A [ k ] 便求了出来：

A[k]=n−kTarrive A [ k ] = n − k T a r r i v e

现在考虑释放锁的过程导致的状态转换。

先理解状态 S[k] S [ k ] 的意义， S[] S [ ] 这里是的是Service，相应的对应 A[] A [ ] 则表示Arrival，所谓的服务时间指的是从当前CPU获得spinlock到该spinlock成功转给下一个CPU之间的时间！这部分时间包括两个部分，一个部分是执行lock/unlock之间代码的时间 E E ，另一部分时间指的是unlock操作中消耗的时间，我们把这部分时间设为 R R ，现在的问题转化为根据以上的信息，求出 R R 的表达式。

我们在讨论中有个假设，即我们思想实验的平台对cache一致性中update的管理方式是点对点one by one的unicast方式，而不是broadcast的方式，设处理一个CPU的update时间为 c c ，那么在 k k 个CPU同时自旋等锁的条件下，所有的CPU的cache line全部更新的时间就是 k×c k × c ，由于ticket spinlock是严序的，而cache line update的到达先后却不可控制，因此下一个获得锁的CPU的cache line得到更新的时间平均值为 k×c2 k × c 2 ，即平均在这个时间后，下一个CPU即可以成功获取锁，从spin_lock自旋状态返回。于是，我们有：

S[k]=1E+k×c2 S [ k ] = 1 E + k × c 2

以上关于 A[k] A [ k ] 和 S[k] S [ k ] 的表达式非常好理解，我们可以看到，请求的到达速率，即spin_lock的速率是和空闲CPU数量，即不在自旋状态的CPU数量成正比的，显然地，空闲CPU越多，请求越容易到达，相反，spin_unlock的速率，即 S[k] S [ k ] ，则是和当前自旋状态的CPU数量成反比的，至少是负相关的，因为自旋状态的CPU越多，更新这么多CPU的cache line的时间开销就越大，这意味着服务速率S[k]就会越小。

有了上面基本的结论，加上下面一个稳态下Markov chain状态转换率守恒的基本原则，就可以导出模型本身了：

设，P0,P1,...Pn是系统处在这n个状态的概率，显然ΣPk=1。当系统处在稳态时，下面的式子成立： 设 ， P 0 , P 1 , . . . P n 是 系 统 处 在 这 n 个 状 态 的 概 率 ， 显 然 Σ P k = 1 。 当 系 统 处 在 稳 态 时 ， 下 面 的 式 子 成 立 ：
Pk×A[k]=Pk+1×S[k] P k × A [ k ] = P k + 1 × S [ k ]

【这里非常感谢阿里云的哥们儿帮我拉了一位数学界的大牛群聊，让我对Markov chain的状态转换率有了更深的理解！】

这是一个递推的开始，我们可以求出 Pk P k 关于 k k 的表达式，然后模型里的参数就可以去用实际值填充了。具体过程不在这里罗列，最终通过上面的三个式子推导出来的公式为：

Pk=1Tkarrive(n−k)!∏ki=0(E+ic)∑ni=01Tiarrive(n−i)!∏ij=0(E+jc) P k = 1 T a r r i v e k ( n − k ) ! ∏ i = 0 k ( E + i c ) ∑ i = 0 n 1 T a r r i v e i ( n − i ) ! ∏ j = 0 i ( E + j c )

有了这个式子，我们便可以求出任意时刻系统中处在自旋等锁状态的CPU总量：

C=∑ni=0iPi C = ∑ i = 0 n i P i

模型最终在于解释历史数据和预测未来数据，在上面的基础上，我们导出一个加速比的概念，即在 x x 个CPU的系统中争抢特定的sinlock，CPU总量 x x 中有多少CPU未处在自旋等锁的状态。显然，它的值为：

S=x−C S = x − C

如果随着 x x 的增加， S S 也增加，这意味着增加了CPU核心数量确实缓解了spinlock带来的串行化问题，但是不幸的是，情况并非如此。该模型显示出的 S/x S / x 曲线显示出当总CPU数量 x x 增加到一定程度，加速比会断崖跌落(CPU太多了，one by one的cache line操作太重太耗时了！)，这意味着在达到某种条件的情况下，增加CPU核心数量反而会损害系统性能！

不可伸缩也就罢了，cache line的操作没想到影响如此之大！

关于Markov chain spinlock模型的推论

我们再看 S[k] S [ k ] 的表达式：

S[k]=1E+k×c2 S [ k ] = 1 E + k × c 2

这个式子是spinlock不可伸缩的根源。注意这里的 E E ，它对spinlock整体不可伸缩性的程度的影响至关重要！我们进一步可以将式子抽象为：

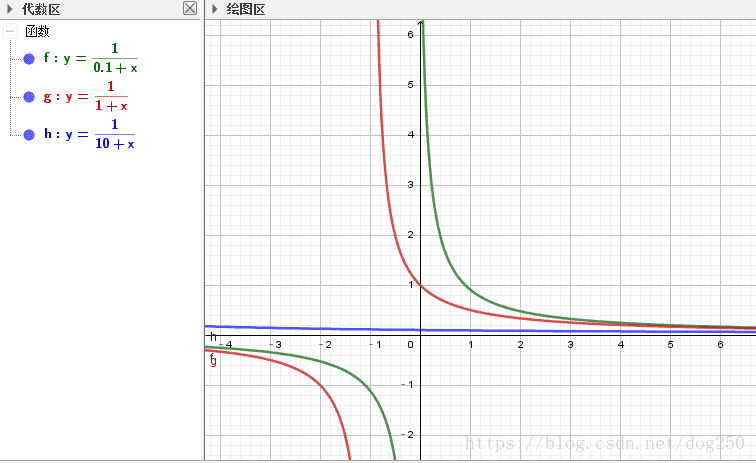
f(x)=1α+x f ( x ) = 1 α + x

然后我们来看一下 x/y x / y 曲线的走势：

回到我们的模型， E E 越大，cache一致性时间线性增长的影响就越不明显，只有在 E E 比较小的时候，我们才深受spinlock不可伸缩之害。然而spinlock的应用场合不就是critical section很小的时候吗？呜呼！

假设我们的critical section确实很小，那么 S[k] S [ k ] 和 k k 之间就近似反比关系了，这样事情就严重多了。它的根源在于cache一致性的时间是 O(n) O ( n ) 的而不是常数级 O(1) O ( 1 ) 的，因此我们也就有了解决问题的方向。下一节详述。

<参考文献：Non-scalable locks are dangerous>

MCS spinlock如何解决问题

问题已经很明确，如何破解显然已经不是重要的事了。

既然问题出在公共共享变量上自旋导致的cache一致性时间开销太大，那么改成在私有变量上自旋即可，这显然是一个 O(1) O ( 1 ) 的操作，替掉之前不可伸缩的 O(n) O ( n ) 操作即可。

为了做到这一点，需要重新设计spinlock的数据结构。本节所描述的新的spinlock正是业内有名的MCS spinlock，一些简单的介绍请参考下面的文章：
MCS locks and qspinlocks：https://lwn.net/Articles/590243/

OK，让我们从代码的角度来看一下为什么MCS spinlock可以解决cache一致性导致的non-scalable问题。

mcs spinlock在Linux的实现在kernel/locking/mcs_spinlock.h文件，不过直到4.14版本内核，Linux并没有哪个子系统采用这个新的spinlock，不管怎样，既然代码在手，我们便可以自己用。

和ticket spinlock的描述一致：

• 定义MCS spinlock

struct mcs_spinlock {
    struct mcs_spinlock *next; // 类似ticket的概念，所有争锁排队
    int locked; /* 1 if lock acquired */ // 本地的自旋变量，不再是全局
};

可见其创举在于在自旋变量纳入了排队实体本身。在mcs spinlock中，一个struct mcs_spinlock实例就是一个排队实体，它拥有自己的自旋变量locked，即它只需要不断check自己的locked变量即可。这体现了OO的思想。

• MCS spinlock上锁

// 自己的排队节点node需要自己在外部初始化，它将被排队到lock指示的等锁队列中。
void mcs_spin_lock(struct mcs_spinlock **lock, struct mcs_spinlock *node)
{
    struct mcs_spinlock *prev;

    /* Init node */
    node->locked = 0;
    node->next   = NULL;
    // 原子执行*lock = node并返回原来的*lock
    prev = xchg(lock, node);
    if (likely(prev == NULL)) {
        return;
    }
    // 原子执行 prev->next = node;
    // 这相当于一个排入队的操作。记为(*)
    WRITE_ONCE(prev->next, node);

    while (0 == &node->locked)
        ; // 在自己的locked变量上自旋等待！
}

没啥说的。

• MCS spinlock解锁

// 自己要传入一个排入到lock的队列中的自己的node对象node，解锁操作就是node出队并且主动将队列中下一个对象的locked帮忙设置成1.
void mcs_spin_unlock(struct mcs_spinlock **lock, struct mcs_spinlock *node)
{
    // 原子获取node的下一个节点。
    struct mcs_spinlock *next = READ_ONCE(node->next);

    if (likely(!next)) {
        // 二次确认真的是NULL，则返回，说明自己是最后一个，什么都不需要做。
        if (likely(cmpxchg_release(lock, node, NULL) == node))
            return;
        // 否则说明在if判断next为MULL和cmpxchg原子操作之间有node插入，随即等待它的mcs_spin_lock调用完成，即上面mcs_spin_lock中的(*)注释那句完成以后
        while (!(next = READ_ONCE(node->next)))
            cpu_relax_lowlatency();
    }
    // 原子执行next->locked = 1;
    arch_mcs_spin_unlock_contended(&next->locked);
}

你已经看到了，unlock操作仅仅操作了next的locked字段，该字段属于在某个CPU上自旋等待的mcs spinlock对象，不会触发全局的cache一致性刷新！

上述的mcs spinlock实现，之所以解决了保证cache一致性而导致的开销随着CPU核数的增加线性增加的问题，就是因为一个简单的动作，即传球代替了抢球。ticket spinlock的问题在于，既然你已经知道谁是下一个获得锁的等待者，为什么不直接将控制权交给它呢？为什么还要有一个全局盲抢的动作呢？

---

告一段落？No！

---

也许你已经看到了当前Linux的MCS spinlock的实现问题，它的API变了，这意味着你无法对内核中已经使用的ticket spinlock进行无缝替换。我们需要下面的API：

void mcs_spin_lock(struct mcs_spinlock *lock);
void mcs_spin_unlock(struct mcs_spinlock *lock);

Ahha，由于同一个CPU同时只能等待一个spinlock，这件事就很简单了。来吧，让我们实现它：

struct mcs_spinlock_node {
        struct mcs_spinlock_node *next;
        int locked; /* 1 if lock acquired */
};

struct mcs_spinlock {
        struct mcs_spinlock_node nodes[NR_CPUS];
        struct mcs_spinlock_node *tail;
};


void mcs_spin_lock(struct mcs_spinlock *lock)
{
        struct mcs_spinlock_node *local;
        struct mcs_spinlock_node *prev;
        int cpu = smp_processor_id();

        local = &(lock->nodes[cpu]);
        local->locked = 0;
        local->next = NULL;

        prev = xchg(&lock->tail, local);
        if (prev == NULL) {
                return;
        }
        WRITE_ONCE(prev->next, local);

        while (!local->locked); 
}

void mcs_spin_unlock(struct mcs_spinlock *lock)
{
        struct mcs_spinlock_node *local;
        struct mcs_spinlock_node *next;
        int cpu = smp_processor_id();

        cpu = smp_processor_id();
        local = &(lock->nodes[cpu]);
        next = READ_ONCE(local->next);

        if (likely(!next)) {
                if (cmpxchg_release(lock->tail, local, NULL) == local) {
                        return;
                }
                while (!(next = READ_ONCE(local->next)));
        }

        local->next->locked = 1;
}

Look at this.是不是好看了很多呢？

好了，关于spinlock的话题差不多该结束了。贴出几篇我之前关于自旋锁的文章以体现延续性吧：
新的排队spin_lock–有序和无序：https://blog.csdn.net/dog250/article/details/5303249?locationNum=10&fps=1
自旋锁的枝枝蔓蔓：https://blog.csdn.net/dog250/article/details/5302886
本地自旋锁与信号量/多服务台自旋队列-spin wait风格的信号量：https://blog.csdn.net/dog250/article/details/47098055
一个Linux内核的自旋锁设计-接力嵌套堆栈式自旋锁：https://blog.csdn.net/dog250/article/details/46921989

<参考文献：MCS locks and qspinlocks>

Aliworkqueue

感谢fcicq大神给介绍aliworkqueue，这是同样优化策略的另一种体现，我还没有测试，但是看其实现感觉略微重量的些。不多说，直接看patch吧：
aliworkqueue: Adaptive lock integration on multi-core platform：https://patchwork.kernel.org/patch/8844841/

Wire-latency(RC delay) dominate modern computer performance,
conventional serialized works cause cache line ping-pong seriously,
the process spend lots of time and power to complete.specially on multi-core platform.
However if the serialized works are sent to one core and executed
ONLY when contention happens, that can save much time and power,
because all shared data are located in private cache of one core.
We call the mechanism as Adaptive Lock Integration.
(ali workqueue)

此外，这里有一个fcicq大神的解说：
MaLing 离开某厂纪念文 & 介绍 aliworkqueue：https://www.douban.com/note/596489332/

Aliworkqueue除了考虑到了spinlock本身加锁解锁对cache一致性的影响，还考虑到了spinlock保护的critical section操作的共享数据读写对cache一致性的影响，如此一来，本文上述的Markov chain模型就要进行修订了，因为critical section的操作时间不能再被当是常量 E E 了，而它也要作为一个和CPU核数相关的量参与到模型的构建中了。

不多说。

后记

凌晨3点半。豪雨继续中…
黑云压顶白珠跳，浙江温州皮鞋湿。