python之实战----PCA、SVD、（NOnlinear PCA）KernelPCA、战iris

PCA

#-*- coding=utf-8 -*-
import numpy  as np
from sklearn import datasets,decomposition,manifold
import matplotlib.pyplot as plt 

def load_data():
    iris=datasets.load_iris()
    return iris.data,iris.target

def test_PCA(*data):
    X,y=data
    pca=decomposition.PCA(n_components=None)
    pca.fit(X)
    print('explained variance ratio : %s '%str(pca.explained_variance_ratio_))
     
if __name__=='__main__':
     X,y=load_data()
     test_PCA(X,y)

结果是四个特征值的比例4维度降到2维度：

PS E:\p> python test1.py
explained variance ratio : [ 0.92461621  0.05301557  0.01718514  0.00518309]

pca画图

#-*- coding=utf-8 -*-
import numpy  as np
from sklearn import datasets,decomposition,manifold
import matplotlib.pyplot as plt 

def load_data():
    iris=datasets.load_iris()
    return iris.data,iris.target

def test_PCA(*data):
    X,y=data
    pca=decomposition.PCA(n_components=None)
    pca.fit(X)
    print('explained variance ratio : %s '%str(pca.explained_variance_ratio_))

def plot_pca(*data):
    X,y=data  
    pca=decomposition.PCA(n_components=2)#设置降到二维X[0],X[1]
    pca.fit(X)
    X_r=pca.transform(X)#将维度降低应用于X.

    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    '''
    colors=((1,0,0),(0,1,0),(0,0,1),(0.5,0.5,0),(0,0.5,0.5),(0.5,0,0.5),
    (0.4,0.6,0),(0.6,0.4,0),(0,0.6,0.4),(0.5,0.3,0.2),)
    这里只用到前三个，因为我们知道鸢尾花数据集的特点
    '''
    colors = ['navy', 'turquoise', 'darkorange']
    for label,color in zip(np.unique(y),colors):
        #unique（）保留数组中不同的值
        position=y==label
        ax.scatter(X_r[position,0],X_r[position,1],label="target= %d"%label,color=color)

    ax.set_xlabel("X[0]")
    ax.set_ylabel("X[1]")
    ax.legend(loc="best")
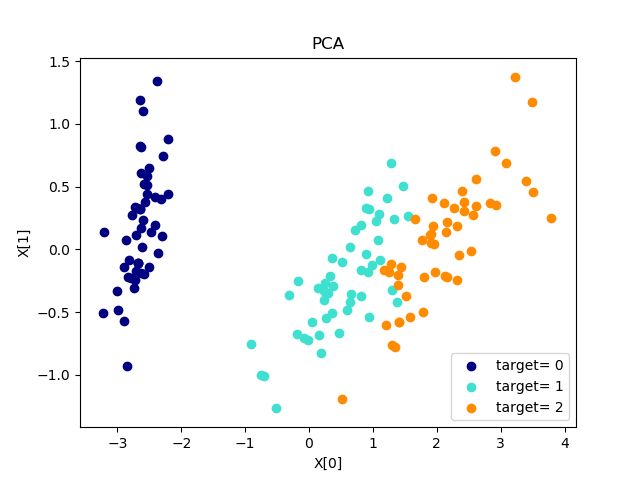
    ax.set_title("PCA")
    plt.show()
if __name__=='__main__':
    X,y=load_data()
    plot_pca(X,y) 

结果：