博客作业06--图

1.学习总结(2分)

1.1图的思维导图

图的存储结构--图的遍历---最小生成树--最短路径---拓扑排序、关键路径，这些知识点需要都梳理。

1.2 图结构学习体会

谈谈你对图结构中的几个经典算法学习体会。具体有：

• 深度遍历算法:从顶点v出发，以纵向方式一步一步向后访问其未访问邻点w，再从访问的点w进行深度遍历其余顶点，采用递归方法。
• 广度遍历算法：从顶点v出发，以横向方式一步一步向后访问未访问的邻点v1,v2,v3....再按照v1，v2，v3次序访问每个顶点的所有未访问邻点，采用队列方法。
• Prim和Kruscal算法：Prim算法是直接查找，多次寻找邻边的权重最小值，而Kruskal是需要先对权重排序后查找的。
• Dijkstra算法：使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。
• 拓扑排序算法：将无向图G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。

2.PTA实验作业（4分）

2.1 题目1：7-1 图着色问题

2.2 设计思路（伪代码或流程图）

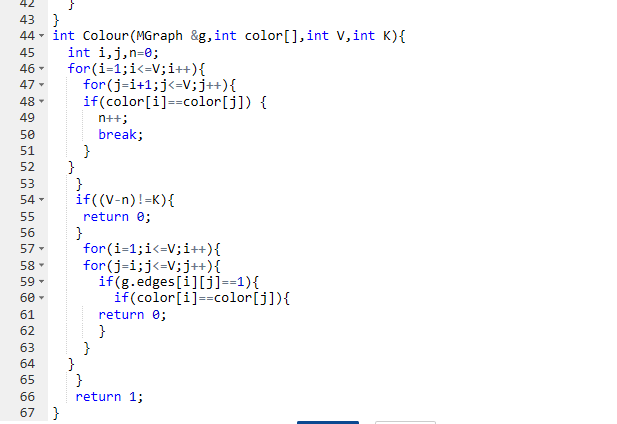
用邻接矩阵保存邻接点
定义color数组保存每个顶点的颜色
从顶点1开始依次遍历与其相邻点，并比较两者color数组的颜色是否相同
IF 相同    return 0;
ELSE IF 颜色数不一致 return 0;
return 1;

2.3 代码截图

2.4 PTA提交列表说明。

未注意到序号从1开始导致数组大小不足，将最大值改为501即可。

2.1 题目2：7-2 排座位

2.2 设计思路（伪代码或流程图）

用邻接矩阵保存两人关系初始值为0，朋友值为1，敌人为-1
把关系为朋友的所有人插入到同一头节点的链表中
对需要判断的两人
IF 邻接矩阵中两人不为敌人且处于"朋友链”中，则输出No problem
ELSE IF 邻接矩阵中两人既非朋友亦非敌人且不处于"朋友链”中，则输出 ok
ELSE IF 邻接矩阵中两人为敌人但处于"朋友链”中，则输出 ok  but
ELSE IF 邻接矩阵中两人为敌人且不处于"朋友链”中则输出no way

2.3 代码截图

2.4 PTA提交列表说明。

对于输出结果的判断条件不准确，并且输出的结果打错了。解决：重新判断输出条件并进行提交尝试

2.1 题目3：7-3 六度空间

2.2 设计思路（伪代码或流程图）

用邻接表保存邻接点
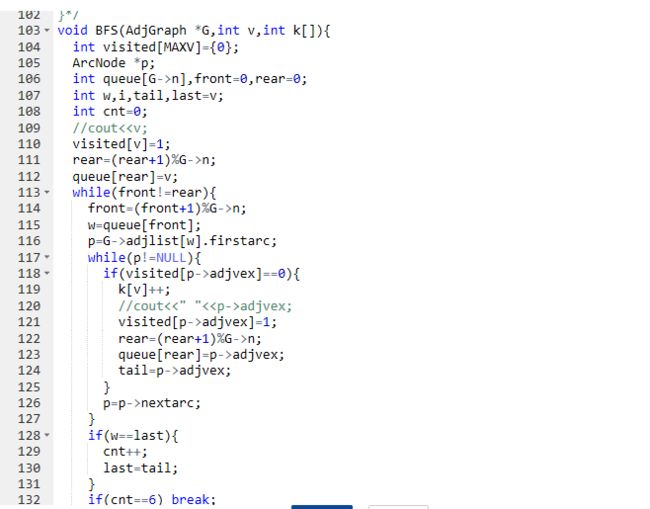
修改广度遍历函数
当队列不为空时循环
设置last变量保存遍历每层时最后一个点，变量cnt=0表示层数，设置数组k保存每个顶点满足条件的点的个数
若出队时的点是last变量保存的层最后一个点，层数cnt++
IF cnt==6 退出循环

2.3 代码截图

2.4 PTA提交列表说明。

用last变量直接保存了当前队列访问节点作为每层最后节点导致错误，解决：设置tail变量表示当前节点，并判断条件出队列的元素是否和last变量一致，若一致则赋给last表示每层最后的点

3.截图本周题目集的PTA最后排名（3分）

本次题目集总分：170分

3.1 PTA排名（截图带自己名字的排名）

3.2 我的总分：1.5分

4.阅读代码（必做，1分）

#include 
#include 
 
#include "graph.h"
 
#define TEST_SIZE (6)
 
 static void
match_sink(Graph g, int source, int sink, void *data)
{
    assert(data && sink == *((int *) data));
}
 
static int node2dot(Graph g)
{
    assert(g != NULL);
    return 0;
}
 
static void print_edge2dot(Graph g,int source, int sink, void *data)
{
    fprintf(stdout,"%d->%d;n",source,sink);
}
static int edge2dot(Graph g)
{
    assert( NULL);
    int idx = 0;
    int node_cnt = graph_vertex_count(g);
    for(idx = 0;idx

结合了邻接矩阵和邻接表，实现了动态分配数组，长度可以扩展，既不浪费空间，有不会带来性能损失。