第六章 FP-Growth算法
海量数据下,Apriori算法的时空复杂度都不容忽视。
1)空间复杂度:如果L1数量达到104的量级,那么C2中的候选项将达到107的量级。
2)时间复杂度:每计算一次Ck就需要扫描一遍数据库。
此时,人们希望设计一种方法,“挖掘全部频繁项集而无须这种代价昂贵的候选产生过程”。一种试图这样做的有趣的方法称为频繁模式增长(FP-Growth)。它采取如下分治策略:首先,将代表频繁项集的数据库压缩到一颗频繁模式树(FP树),该树仍保留项集的关联信息。然后,把这种压缩后的数据库划分成一组条件数据库,每个数据库关联一个频繁项或“模式段”,并分别挖掘每个条件数据库。
1 FP-Growth算法的基本介绍
FP-Growth算法:在不生成候选项的情况下,完成Apriori算法的功能。只需要对数据库进行两次扫描,它发现频繁项集的基本过程如下:
1)构建FP树
2)从FP树中挖掘频繁项集
FP-Growth算法的基本数据结构,包含一棵FP树和一个项头表。
2 构建FP树
2.1 项头表的构建
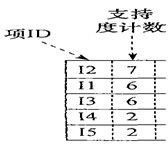
以上图这个事务数据库为例。
数据库的第一次扫描与Apriori算法相同,它导出频繁1-项集的集合,并得到它们的支持度计数(频度)。设最小支持度计数为2。频繁项的集合按支持度计数的递减序排序。结果集或表记为L。这样,有L={{I2:7},{I1:6},{I3:6},{I4:2},{I5:2}}。
2.2 FP树的构建
首先,创建树的根节点,用“NULL”标记。第二次扫描数据库D。每个事务中的项都按L中的次序处理(即按递减支持度计数排序),并对每个事务创建一个分枝。例如,第一个事务“T100:I1,I2,I5”包含三个项(按L中的次序I2、I1、I5),导致构造树的包含三个结点的第一个分枝
扫描所有的事务后得到的树显示在下图:
3 从FP树中挖掘频繁项集
3.1 抽取条件模式基
条件模式基:以所查找元素项为结尾的路径集合。简而言之,一条前缀路径就是介于所查找元素与树根结点之间的所有内容。
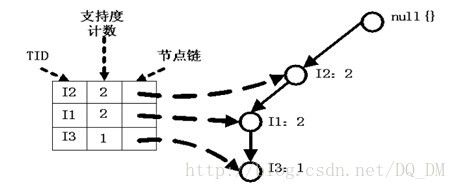
例如,I3在FP树中一共出现了3次,其祖先路径分别是{I2,I1:2},{I2:2}和{I1:2}。这3个祖先路径的集合就是频繁项I3的条件模式基。
3.2 创建条件FP树
条件树:将条件模式基按照FP树的构造原则形成一个新的FP树。比如上图中I3的条件树就是:
3.3 产生频繁项集
首先考虑I5,它是L中的最后一项,而不是第一项。从表的后端开始的原因随着解释FP树挖掘过程就会清楚。I5的条件模式基是{{I2, I1:1}, {I2 ,I1,I3:1}},I5构造得到的条件FP-树如下。
这个条件FP-树是单路径的,直接列举{I2:2,I1:2,I3:1}的所有组合,之后和模式后缀I5取并集得到支持度大于2的所有频繁模式:{I2,I5:2},{I1,I5:2},{I2,I1,I5:2}。
对于I4,方法类似。
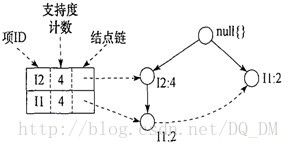
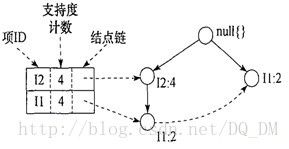
对于I3,条件模式基是{{I2,I1:2}, {I2:2}, {I1:2}}。它的条件FP树是:
FP树有两个分枝
这是一个单路径的条件FP树,在FP_Growth中把I2和模式后缀{I1,I3}取并得到模式{I2,I1,I3:2}。理论上还应该计算一下模式后缀为{I2,I3}的模式集,但是{I2,I3}的条件模式基为空,递归调用结束。最终模式后缀I3的支持度大于2的所有模式为:{I2,I3:4},{I1,I3:4},{I2,I1,I3:2}。
对于I1,方法类似。
4 FP-Growth的伪代码
5 FP-Growth的优劣势
FP-Growth方法将发现长频繁模式的问题转换成在较小的条件数据库中递归地搜索一些较短模式,然后连接后缀。它使用最不频繁的项作后缀,提供了较好的选择性。该方法显著地降低了搜索开销。
当数据库很大时,构造基于主存的FP树有时是不现实的。
对FP-Growth方法的性能研究表明,对于挖掘长的频繁模式和短的频繁模式,它都是有效的和可伸缩的,并且大约比Apriori算法快一个数量级。
了解更多请参见PPT