【QBXT】学习笔记——Day11网络流

网络流，真是一个有趣的课题呢。
经历了数学的折磨后，感觉世界真美好。珍爱生命，远离数论

====================分割线========================

Day11 1.25AM

网络流的基本操作在此也没什么好说的。
要掌握的应该也就是dinic或者SAP(ISAP)+费用流算法。
主要难点还是在建模上。接下来就是一堆题目。

POJ2391 Ombrophobic Bovines
有 F F 个地方，每个地方有一定数量的牛，能够容纳一定数量的牛，某些地方之间有边，表示走两点之间需要消耗的时间。
现在求使得所有的牛都被容纳所需要的最少的时间。
时间是不确定的，所以我们二分答案。
对一堆点，如果最短路不超过二分的答案，则在其拆出道点之间连边，容量INF。满流则可行。
不拆点会挂的，因为可能会在任意连边点中流来流去。
拆点是为了分层。

POJ1149 PIGS
有 N N 个顾客，有 M M 个猪圈，每个猪圈有一定的猪，在开始的时候猪圈都是关闭的，
顾客来买猪，顾客打开某些猪圈，并可以在其中挑选一定的猪的数量，
在这个顾客走后，可以在打开的猪圈中将某个猪圈的一些猪牵到另外一个打开的猪圈，
然后所有的猪圈会关闭，这样下一个顾客来了继续上面的工作。

发现单位流量应该是表示猪的，先考虑朴素模型。
一共 n n 轮交易，那么建 n n 排点，每排 m m 个，代表每轮交易之前段猪圈，再对n个顾客设点。
对于每个顾客向汇连边，容量为购买上限。
源向第一轮猪圈连，容量为初始数量。
对于 i i 个顾客能打开的猪圈，从第i轮的这些猪圈向该顾客连边，容量INF，
同时向第 i+1 i + 1 轮的这些猪圈连边，容量INF。
显然是爆炸的。

网络流的常用的建模考虑手段是优化增广路。

分开考虑每个猪圈，考虑对其产生影响的顾客。
只有这些顾客才能买，也只有他们才能移动猪圈的猪。
那么从元向每个猪圈的第一个顾客连边，容量为初始数量。
每个猪圈的第 i i 个顾客向第 i+1 i + 1 个顾客连边，容量INF。
模型等价，而我们的建模进一步省略了猪圈。

也可以这样想：考虑到实际上顾客对猪有调配权。
假设顾客1能买A/B/C的猪圈，顾客2能买C/D猪圈。
那么实际上顾客2能买到A/B/C/D，因为顾客1可以将剩余的猪调配到C
这就是上面建模的思想。

POJ3281 Dining
有 F F 种食物, D D 种饮料， N N 头奶牛,每头牛有自己的喜欢的和食物和饮料。
一种食物被一头牛吃了之后,其余牛就不能吃了。
如果食物就是二分图匹配。现在大概是一个三分图？
我们对牛拆点限流即可。

最小割
增广路上每一条路，代表一个破石头门的 选择。

最大流>=最小割
此时不存在增广路，因此最大流是一个割。
最小割>=最大流
任意一个割的容量>=最大流
因此最大流=最小割。
意识流证明？

Escape
有一条山谷，长度为 W W ，宽度为 L L ，有 n n 个哨兵，第 i i 个哨兵的视野为以其位置为圆心半径为 ri r i 的圆。
现在要从山谷最左走到最右而不进入任何一个哨兵视野，问最少需要提前解决多少个哨兵。

考虑到能通过，即为上下边界之间不连通，转化为最小割模型。
上边界为源，下边界为汇。
对哨兵建点，将哨兵拆成两个点，左入右出，容量为1的边。
我们考虑我们在哨兵之间怎么连边？只要两个哨兵的视野范围重合就要连。
边权为无穷大，意味着不能割这个点，分别从出点向对方的入边连边。
如果哨兵视野和上边界碰到了，就从源向入连1。
如果和下边界碰到，就从出向汇连1.

BZOJ2561 最小生成树
一张 n个点m n 个 点 m 条边的图，每条边有边权。
现在在点 u和点v u 和 点 v 之间连一条权值为L的边，
我们要使这条边既能出现在最小生成树上，又可以出现在最大生成树上。
问要满足这一条件要删去多少条边。

显然对于最小生成树和最大生成树要删掉的边，没有交集。
删掉最少的边，使点 u和点v u 和 点 v 不连通，显然是最小割。
u u 作为源， v v 作为汇，比它大的边加入图，跑最小割。
小的同理，两次结果之和即为答案。

最小权闭合子图：
通常用来描述有依赖关系的若干物品的选择与否，其本质上是最小割。
假设n个物品，每个物品有自己的收益，收益可能为负。
视从S可达到点为选择，可达T的点为不选择。
S->收益为正的物品：收益，
收益为负的物品->T：收益的绝对值。
如果a依赖于b，那么b->a:INF
答案为所有收益为正当物品的收益之和减去最小割。

考虑一条增广路来证明。

NOI2006最大获利(万恶之源)
有 n n 个中转站的选址，在第i个地址处建造中转站的代价为 pi p i 。
有 m m 个用户，第i个会在 ai a i 和 bi b i 个中转站之间通讯，用户愿意支付 ci c i
求建造方案，使获利最大。

CEOI2008 Order
有 n n 个项目和 m m 台机器，每个项目依赖于一些机器。
项目有正的收益，机器可以买也可以租，都有各自代价。借一次机器可以给一个项目用一次。
求最大收益。

CF331E Biologist
有 n n 个点，每个点可以是白色或者黑色，可以花 vi v i 的代价改变第 i i 个点的颜色。
有 m m 个条件，每个条件都是要求某一些点都是某种颜色。
如果满足第 i i 个条件可以获得 gi g i 的收益，否则付出 li l i 的代价。求最大收益。

考虑没有条件，我们用网络流表示状态。
一个点跟源相连表示黑：代价，跟汇相连表示白：代价。
如果一个点最终是黑色的，那么它和汇的权是0，和源是代价。（考虑割边即为不满足）

割点边相当于改变颜色，割条件边相当于放弃条件。
因此我们也可以对条件建点。条件->点，INF，表依赖关系。
如果条件是黑色， S S ->条件：收益+代价。条件->点：INF
如果条件是白色，条件-> T T ：收益+代价。点->条件：INF

正确性证明考虑增广路：
如果有一个点要改颜色，必然会有一条增广路是S->黑条件->点->白条件->T
那么由于条件与点之间的权是INF，因此必然会割掉其中一条边，表示放弃。
剩余的证明类似。

下面是一类经典问题

二元费用问题
有 n n 个点，选和不选各自有收益。有 m m 个条件，有三类（就是 x/y/w x / y / w 不一定相同）：
如果 x和y x 和 y 都选了，获得 w w 的收益。
如果 x和y x 和 y 都没选，获得 w w 的收益.
如果 x和y x 和 y 一个选了一个没选，付出 w w 的代价。
求最大收益。
这里没做笔记，不然跟不上，就贴图吧。

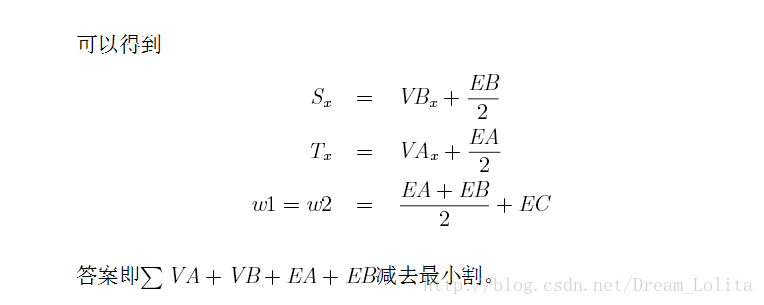
平面图对偶图
对于一个平面图，汇形成一个个小区域，再从源向汇连一条边，形成多一个域。
对于每一个域，作为一个点（包括无限域），将相邻的点连边，就形成了一个对偶图：
无限域作为T，原来的源汇边新构成的域作为S。
易得对偶图的对偶图就是原平面图。
然后我们求原图的最小割，相当于求对偶图的最短路。
就像这幅图，其中蓝色是原图，紫红色？是对偶图。

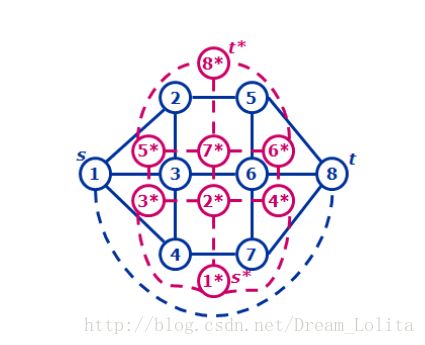
下面是一道很好的题，不过因为在切一道ltq发出来的JOI题，然后就没做，后来看看十分妙啊。

关键在于怎么转化问题，我们可以发现，最暴力的方法拆点后，我们求一个最小割，割的肯定是自己本身拆开的点。因为这条边的流量比较小。
问题就转化为了求对偶图的最短路。
至于这个对偶图怎么构，边权是什么，就要考虑八连通时最短路的东西。
在这里就不说了。

Day11 1.25PM

接下来是费用递增模型：这类模型是一类费用流模型，它代表着某个东西可以选择若干次，而次数每加1所需要的代价是递增的。一种常见情况是选择 x x 的代价为 x2 x 2 。

BZOJ1449(JSOI2009)
有 n n 支球队，有些球队之间已经打了一些比赛了，现给出每个球队的数据 win、lose、C w i n 、 l o s e 、 C 和 D D ，
分别表示已胜场数、已负场数，以及计算收益的两个系数。一支球队的收益为 Cw2+Dl2 C w 2 + D l 2 ，
其中 w w 和 l l 是最后胜负的场数。接下来还有 m m 场比赛。
给出接下来 m m 场比赛的对阵情况，求出 n n 支球队收益和的最小值。
接下来 m m 场比赛的胜负是你可以决定的。

单位的流量代表什么？可以表示胜负关系。
对于n支球队和m场比赛各建一个点，从源向每场比赛连流量1费用0的边，
从比赛向参与这场比赛的两支队伍各连一条流量1费用0的边。剩下的就是队伍收益的费用表示了.
我们球队连向汇的边要表示费用。但因为每一次的增量是不同的，所以还要多加考虑。
如果我们不看负场，只看正常带来的收益。
那么我们就看这个球队接下来会赢多少场，然后每个胜场数连边。
这样我们每次选择的一定是费用最小的，然后是次小的，这样可以保障收益代表的胜场单调。
现在再考虑负场，那么在 w++ w + + 的时候， l−− l − − ，显然前者的上升会更快，所以显然还是一个单调过程。
这样建模就没了。

BZOJ1070(SCOI2007)
有 n n 辆车和 m m 名修理工，一名修理工在一个时刻只能修一辆车，并且在修完一辆之后才能开始修下一辆。
已知每位修理工修每辆车的时间，求顾客的最小平均等待时间。顾客的等待时间为他的车被修好的时间。

首先假设方案是确定的，我们很容易可以得到解。
然后其实对于每一辆车，它的修的顺序越靠后，费用越少，但我们无法确定一共有多少车。
如果我们直接跑最短路，可能会先选到了后面的。
但是对于第 i i 辆车，花费是 k−i+1 k − i + 1 倍，而第 k−i+1 k − i + 1 辆车，花费是 i i 倍。

把每个工人拆成 N N 个点。记为 A[i,j] A [ i , j ] 表示第 i i 个工人修倒数第j辆车。
每个车跟所有 N∗M N ∗ M 个工人拆出的点连边。流量为1，费用为 time[i,j]∗k t i m e [ i , j ] ∗ k 。
源和每辆车连边， N∗M N ∗ M 个点和汇连边，流量都为1，费用同为0。
等价于每个车有一个修车名额，然后塞进师傅的时间槽里。

为什么是对的呢？
考虑第i个工人，他修第j辆车只对后面要修的车有影响，而前面修过的车已经对当前没有影响了。
而这个影响就是后面每个将要修理的车都多等待了time的时间。
其他边流量都为1是显然的，每辆车修一次，每个工人一个时段只能修理一辆车。

BZOJ2879 NOI2012美食节
上一题的加强版。解释相对上一题。
考虑优化上一题的建点，有很多点是没有用的。
那么我们每修一辆车加一个点，丢一个点，保证点数是 m+n m + n
我们动态来建这个图就行了。

BZOJ2597(WC2007)剪刀石头布
有 n n 个人，两两之间进行一次比赛。有些比赛已经进行了，有些还没有。
我们用一个竞赛图来表示输赢情况，一场比赛的有向边从输家连向赢家。
你可以决定尚未进行的比赛的输赢情况，使得下面这种三元组的数量最多：
(a,b,c) ( a , b , c ) 表示一个无序三元组（ (a,b,c) ( a , b , c ) 的任意排列都算同一种），
其中存在有向边 a−>b,b−>c,c−>a a − > b , b − > c , c − > a 。需要输出方案。 n<=100 n <= 100

如果合法，一定会有一个人赢一次，输一次，也就是要找度为2的。
方案数只和度数有关。但是直接算合法似乎不太好算，考虑算不合法的情况。
如果这个点入度为 di d i ，不合法就是 C2di C d i 2 。
这样总的答案就是 C3n−∑C2di C n 3 − ∑ C d i 2
然后把这个式子化一下。

C3n−∑C2di==C3n−12∑(di(di−1))C3n+12∑di−12∑d2i(43)(44) (43) C n 3 − ∑ C d i 2 = C n 3 − 1 2 ∑ ( d i ( d i − 1 ) ) (44) = C n 3 + 1 2 ∑ d i − 1 2 ∑ d i 2

我们发现这最后一项带个平方，用前面的方法做就行了。

BZOJ3171(TC2013 R1AL3)
一块 n×m n × m 的地图，每个格子内有一个箭头。
从某个格子出发，沿着箭头的方向走，从一侧出来边界就从另一侧进入。
如果从任意一个格子出发能回到出发点各自，那么地图合法。
给点地图，求至少要改变几个格子的箭头方向，才能使地图合法。

如何才能使这个图合法？——每个格子入度和出度都为1
那么这个箭头有四个方向可以指，连一条边到当前所指的方向费用是0
考虑改变方向，显然需要花费1的代价。
这样源向每个点的原来的方向连1容量，费用0，对其他三个方向的点连1容量，费用1。
跑一次最小费用最大流，费用即为答案。

TC12432 SRM570 D1L3 CurvyonRails
一块 n×n n × n 的地图，每个格子均为空地或者障碍。
现在要铺铁轨（直的或弯的），每块空地都要被覆盖，每条路线必须闭合，且不能相交。
有些空地上住着弯星人，在这种空地上铺一块直的铁路需要花费1的代价。
给定地图，求是否能够铺铁轨，以及最小代价。

首先还是判断一下有没有解。
显然每个点的度数还是2，这又是一个网格图。那么我们就可以常规操作：
(对偶图)黑白染色。
有解即，存在一些不相交的回路可以覆盖所有空地且不覆盖任意障碍。
也即，每个空地向相邻的空地连出恰好两条轨道。
那么构建网络流模型。
对空地黑白染色，从源向黑点、从白点向汇连容量为2的边。
从黑点向相邻的白点连容量为1的边。满流即有解。

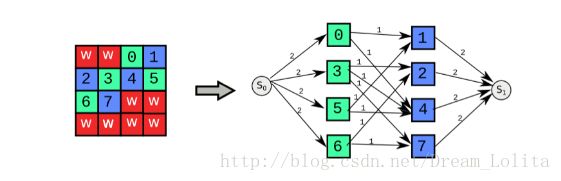
在已有的网络流模型基础上改进。
把每块空地拆成两个点，一个代表横向，一个代表纵向。
横向点向横向相邻的空地的横向点连一条容量为1的边，纵向的类似。满流即有解。

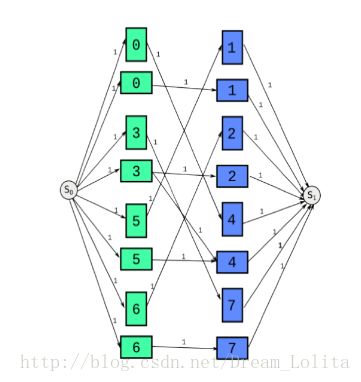
有一个很重要的性质？？
一个弯的轨道是一条横边和一条竖边，一个直到轨道是两条横的或两条竖的。

如果我们强制所有铁轨都是弯的，判断是否有解。
在已有的网络流模型基础上改进。
把每块空地拆成两个点，一个代表横向，一个代表纵向。
横向点向横向相邻的空地的横向点连一条容量为1的边，纵向的类似。满流即有解。

那么现在考虑如何将弯的铁轨变成直的。
那么我们可以把这个弯的铁轨的竖边扭成横边，这
样就在弯的铁轨拆出的横竖边之间加一条流量1费用1的边。
就没了。(码这段的时候感觉怪怪的)

听说接下来是进阶模型？？？
最小割模型。

经典题
BZOJ3144(HNOI2013)切糕
p×q p × q 的网格，每个位置都有 r r 个取值( 1 r 1   r )的选择，每个选择都有各自的代价。
要求四连通相邻的两个位置的差不超过 d d 。问最小代价和。 p,q,r<=40 p , q , r <= 40
对于每个位置的每个选择设点，形成一条链，相邻位置的边的流量为选择的代价。
由于每个位置只能选择一个取值，因此考虑最小割。
现在加入距离限制，距离可以描述为 xi>=xj−d x i >= x j − d 其中 i i 和 j j 相邻。
网络流中的限制通常用无穷大来的边来描述。
因此对于相邻的 (x,y) ( x , y ) 和(x’,y’)已经 d<=k<=r d <= k <= r ，连边 (x,y,k)−>(x′,y′,k′)：INF ( x , y , k ) − > ( x ′ , y ′ , k ′ ) ： I N F
这个图的最小割就是答案。

这题还是很巧妙的，如何表示选择及代价。
用相连两点的边权表示代价，用割边表示选择。
而无穷大的边权依旧表示依赖关系，因为它不可能被割掉。

其实还有一些内容，但是我的硬盘貌似炸掉了，怎么办woc。
赶紧想办法修复硬盘。

总结一下：
如何考虑网络流：先看最暴力的方法，然后挖掘一些性质。
网络流的优化要考虑什么：增广路优化，点数优化，边数优化。
转化问题是很玄学的，是要随缘的。