数据结构与算法题目集（中文） - 7-11 关键活动（30 分）

题目链接：点击打开链接

 

题目大意：略。

 

解题思路：

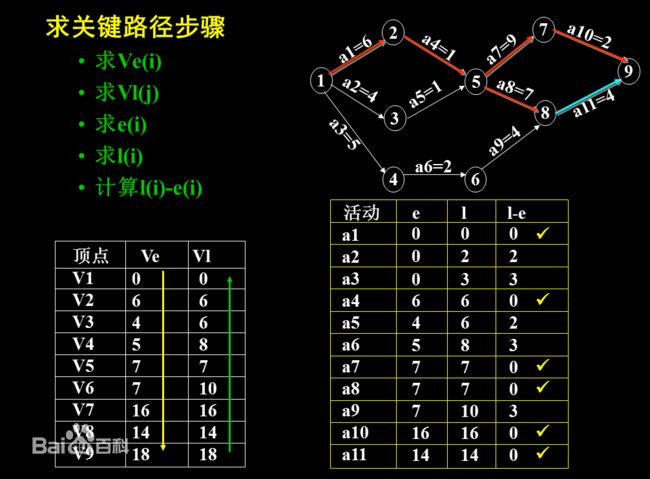
关键路径（最长路径）：AOE网中，顶点被称为事件，而边（或弧）才是活动的描述，边的权值代表活动所花费的时间，因此，事件就是一个活动结束，另一个活动开始的标志，那么要完成整项工程就需要将前面的活动全部完成，所以选最长的路径作为关键路径才能确保工程被完成。

关键路径，注意最后的输出规则。
Ps：关键路径的注意：
* 关键路径上的所有活动都是关键活动，它是决定整个工程的关键因素。
* 关键路径并不唯一。对于有几条关键路径的网，只提高一条关键路径上的关键活动并不能缩短整个工程的工期，只有加快那些包括所有关键路径上的关键活动才能达到缩短工期的目的。
（特殊情况，下面会提到）

 

AC 代码1（传统版）

#include
#include

#define mem(a,b) memset(a,b,sizeof a);
#define INF 0x3f3f3f3f

using namespace std;

typedef long long ll;

const int maxn=200;

int n,m,rs,ans;
int dfn[maxn][maxn], dis[maxn][maxn], mp[maxn][maxn]; // 这里 mp[][] 可以用 dfn[][] 替代
int vl[maxn], ve[maxn], in[maxn], out[maxn]; // ve:vearly  vl:vlate
vector ge[maxn], gl[maxn];

struct node
{
    int s,e,dfn;
}nds[maxn];

void init()
{
    rs=ans=0;
    mem(in,0); mem(out,0); mem(mp,0); mem(vl,INF); mem(ve,0);
    for(int i=0;in2.dfn;
    return n1.s q;
    for(int i=1;i<=n;i++)
        if(!in[i]) q.push(i), ans++;

    while(!q.empty())
    {
        int cur=q.front(); q.pop();
        for(int i=0;i q;
    for(int i=1;i<=n;i++)
        if(!out[i]) q.push(i), vl[i]=rs; // 确保了非最大值的关键路径的除去（技巧）

    while(!q.empty())
    {
        int cur=q.front(); q.pop();
        for(int i=0;i3并不是关键活动，所以如果去了这一条条件代码则是求关键结点；而求关键活动必须要加上这一条
                        if(dfn[i][j] && vl[j]==ve[j] && vl[j]-dis[i][j]==ve[i])
                            nds[k].s=i, nds[k].e=j, nds[k++].dfn=dfn[i][j];
                    }
                }
            }

            sort(nds,nds+k,cmp);

            for(int i=0;i%d\n",nds[i].s,nds[i].e);
        }
    }

    return 0;
}

 

AC 代码2（最短路径版） 

#include
#include

#define mem(a,b) memset(a,b,sizeof a)
#define ssclr(ss) ss.clear(), ss.str("")
#define INF 0x3f3f3f3f
#define MOD 1000000007

using namespace std;

typedef long long ll;

const int maxm=1e4+10, maxn=110;

struct node
{
    int u,v,w;
}es[maxm];

struct nd
{
    int u,v;
}nds[maxm];

int n,m,l,dismax=0;
int dis[maxn], in[maxn], out[maxn], g[maxn][maxn], vis[maxn][maxn];
vector pre[maxn], dv;

int dijkstra()
{
    int f,u,v,w;
    for(int i=1;i<=n;i++) // 最多需要(n-1)条边更新,所以i不能从2开始,要从1开始,多检测一次才知道是否有环
    {
        f=0;
        for(int j=1;j<=m;j++)
        {
            u=es[j].u, v=es[j].v, w=es[j].w;
            if(dis[u]+w>dis[v])
            {
                dis[v]=dis[u]+w;
                dismax=max(dis[v],dismax);
                pre[v].clear();
                pre[v].push_back(u);
                f=1;
            }
            else if(dis[u]+w==dis[v] && find(pre[v].begin(),pre[v].end(),u)==pre[v].end())
                pre[v].push_back(u);
        }

        if(!f) return 1;
    }

    return 0;
}

int cmp(nd n1, nd n2)
{
    if(n1.u==n2.u)
        return g[n1.u][n1.v]>g[n2.u][n2.v];
    return n1.u q;
    q.push(s);

    while(!q.empty())
    {
        s=q.front(); q.pop();
        for(int i=0;i%d\n",nds[i].u,nds[i].v);
    }
    else puts("0");

    return 0;
}