数学小知识点整理（TBC）

前言

感觉距离$scoi2019$的时间不多了博主因为太弱所以现在慌得一批，现在尝试梳理一些小知识点顺便复习。

素数与同余

线性筛部分

常识向，直接贴代码了，大佬们手动跳过吧。
最常用的是线性筛质数。
同时有两种常用的可以线性筛预处理的函数：莫比乌斯函数，欧拉函数。
线性筛代码：

typedef long long ll;
ll prime[N],pri[N],cnt=0,mu[N],phi[N];
inline void init(int len){
	mu[1]=phi[1]=1;
	for(int i=2;i<=len;++i){
		if(!pri[i])prime[++cnt]=i,mu[i]=-1,phi[i]=i-1;
		for(int j=1;i*prime[j]<=len;++j){
			pri[i*prime[j]]=1;
			if(i%prime[j]==0){
				phi[i*prime[j]]=phi[i]*prime[j];
				mu[i*prime[j]]=0;
				break;
			}
			mu[k]=-mu[i];
			phi[k]=phi[i]*(prime[j]-1);
		}
	}
}

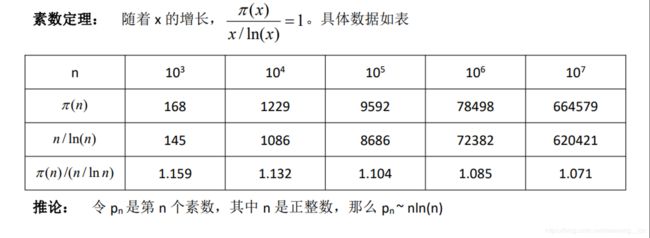
素数

线性递推逆元

指数循环节降幂

当求逆元时模数与求逆元的数有可能不互质时的处理方法

一个神奇的结论

有个结论，对于 m >= 2，与m的互质的数的和为m * phi (m) / 2

拓展欧拉定理

杂乱的一些性质/技巧

二进制枚举子集

这是一个用循环实现的快速枚举子集的方法，代码如下：

for(int i=s;i;i=s&(i-1))

异或前缀和

一个蒟蒻博主听说可以打表证明的性质：
$su{m}_i=i,i\equiv 0\mathrm{m}\mathrm{o}\mathrm{d}4$
$su{m}_i=1,i\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}4$
$su{m}_i=i+1,i\equiv 2\mathrm{m}\mathrm{o}\mathrm{d}4$
$su{m}_i=0,i\equiv 3\mathrm{m}\mathrm{o}\mathrm{d}4$
感觉挺有用的

O(n)预处理popcount

$popcount(x)$指$x$在二进制形式中二进制位为$1$的数量。
直接处理是$O(lo{g}_x)$的，但是可以$O(a_{max})$预处理。
代码：

for(int i=1;i<=lim;++i)Popcount[i]=Popcount[i>>1]+(i&1);

原理很简单（逃

多项式一类

因为太多之前特意写了一篇博客 才不是骗访问量呢

组合数学

卡特兰数通项

$Ca{t}_n=C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}$

斯特林数

两类可以用$fft$预处理做到$O(nlogn)$
但是一般都只用$O(n^2)$（雾
下面给出递推式：
第一类斯特林数递推式：

第二类斯特林数递推式：



第一类斯特林数详细小结
第二类斯特林数详细小结

错排公式

看了这道题你就懂了。
递推式：$f_i=(i-1)(f_{i-1}+f_{i-2})$

二项式反演

$f_n={\sum }_{i=0}^n\left(\genfrac{}{}{0ex}{}{n}{i}\right)g_i$
=>$g_n={\sum }_{i=0}^n((-1{)}^i\left(\genfrac{}{}{0ex}{}{n}{n-i}\right)f_i)$
可以看这道题简单体会一下。