七、改进神经网络的学习方法（3）：过拟合及改进方法（正则化、Dropout）

本博客主要内容为图书《神经网络与深度学习》和National Taiwan University (NTU)林轩田老师的《Machine Learning》的学习笔记，因此在全文中对它们多次引用。初出茅庐，学艺不精，有不足之处还望大家不吝赐教。

1. 过拟合

  费米曾经表明：有大量自由参数的模型能够描述一个足够宽泛的现象。即使这样的模型与现有的数据吻合得很好，这也不能说它是一个好的模型。这仅仅只能说明，有足够自由度的模型基本上可以描述任何给定大小的数据集，但是它并没有真正地洞察到现象背后的本质。这就会导致该模型在现有的数据上表现得很好，但是却不能普及到新的情况上，这样的现象也就是今天的主角之一——“过拟合”。因此判断一个模型真正好坏的方法，是看其对未知情况的预测能力。

1.1 过拟合带来的问题

  下面让我们举例来突出过拟合问题的严重性。假设我们使用有30个隐藏神经元网络，其中含有23860个特征。但是不用全部的50000个 MINST 图像做训练，而仅仅使用前1000个。用较小的训练集能够使突出泛化的问题。此外，我们依然用交叉熵代价函数来训练模型，学习率为 η=0.5 ，mini-batch 的大小选为10。然而，与之前不同的是，我们将要迭代400次，由于使用了较少的训练实例，所以就要较多的训练次数。

  根据结果，我们能绘制训练集上代价函数随迭代次数的变化情况如图1所示

图1. 训练集上代价函数随迭代次数的变化情况

然而测试集上分类正确率随迭代次数的变化情况如图2所示

图2. 测试集上分类正确率随迭代次数的变化情况

在前200步（未显示）准确率上升到接近百分之82，然后学习的效果就逐渐放缓。最后，在280步附近，分类准确率几乎停止改善，之后的学习仅仅在 这个准确率附近有一些小的随机波动。与上一个图表对比，我们会发现，训练数据的代价函数值是持续下降的。如果我们只关注代价函数，模型似乎一直在“改进”。但测试精度结果表明：此时的改进只是一种错觉。因此称此时的网络是过拟合（overfitting）或过训练（overtraining）的。

  或许你会觉得用训练数据的代价函数和测试数据的分类正确率相互比较不是一个直接比较，那么下面将采用测试集上代价函数随迭代次数的变化情况与训练集上的相比，如图3

图3. 测试集上代价函数随迭代次数的变化情况

从图中可以看到，测试数据的代价在15步前一直在降低，之后它开始变大，然而训练数据的代价是在持续降低的。这是另外一个能够表明我们的模型是过拟合的迹象。

  此时，我们遇到了一个难题，到底哪一个才是发生过拟合的关键点，15步还是280步？解答这个问题首先需要回顾在《四、用简单神经网络识别手写数字（内含代码详解）》中提到的，神经元的输出层是10个神经元，把输出层神经元依次标记为 0 到 9，找到拥有最高的激活值的神经元，将它的标记作为神将网络的结果进行输出。举个例子，如果输出神经元的激活值为 a=[0.1,0.4,0.02,0.04,0.09,0.2,0.05,0.8,0.03,0.009] ，则最后的分类结果为 [0,0,0,0,0,0,0,1,0,0] ；假设实际的期望输出是 [0,0,0,0,0,0,0,1,0,0] ，则代价函数的计算公式如下

C(w,b)=\frac1{2n}\sum_x||y(x)-a||^2\tag{1}\label{1}

而计算正确率是计算分类正确的百分比。所以即使测试数据代价函数增加了，但是未必会改变正确率，所以测试数据的代价只不过是分类精度的附属品。因此，在我们的神经网络中，把280步视为模型开始过拟合的转折点。

  在训练数据的分类精度中也可以看到过拟合的迹象如图4所示

图4. 训练集上代价函数随迭代次数的变化情况

测试集上准确率一直上升到100% 。也就是说，网络能正确分类所有训练图像；而与此同时，测试准确率仅为82.27% 。所以我们的网络只是在学习训练集的特性，而不能完全识别普通的数字。就好像网络仅仅是在记忆训练集，而没有真正理解了数字能够推广到测试集上。

1.2 检测过拟合的方法

  在含有大量权重和偏差参数的神经网络中，过拟合是常常会遇到的问题，因此需要一种可以检测过拟合发生的技术。在实际中常常采用验证集来检测过拟合是否发生而不是采用测试集，这样做的目的主要有以下两点

• 普遍使用
  通过validation_data来选择不同的超参数（例如训练步数、学习率、最佳网络结构等等）是一个普遍的策略。

• 防止测试数据过拟合
  如果基于test_data的评估结果设置超参数，有可能我们的网络最后是对test_data过拟合。所以使用验证集检验模型过拟合并找到优秀的参数，在通过训练集评估精度，这样的方法训练出的神经网络往往具有更好的泛化能力，称这种验证数据与测试数据完全分开，并找到优秀参数的方法为分离法（hold out method）

  在确定使用什么样的数据之后就要确定使用什么样的指标来监控模型防止过拟合，从上文中可以看出，带选择的指标有四个，训练数据代价函数、训练数据分类正确率、验证数据代价函数、验证数据分类正确率。其中验证数据代价函数通过前文的分析，其与测试集的分类精度无直接关系且无法判断从哪一点开始过拟合，因此不予采用。其次训练数据代价函数常用来判断训练的速度，收敛情况，因此采用训练数据分类正确率和验证数据分类正确率作为检验模型是否过拟合的指标。在每一 步训练之后，计算validation_data的分类精度。一旦validation_data的分类精度达到饱和，就停止训练，这种策略叫做提前终止（early stopping）。然而在实践中，我们并不能立即知道什么时候准确度已经饱和。因为神经网络在训练的过程中有时会停滞一段时间，然后才会接着改善。取而代之，我们在确信精度已经饱和之前会一直训练 。

2. 改进方法

  避免过拟合的方法主要有三种，增大训练数据数量、减小网络规模和正则化技术。

2.1 增大训练数据数量

  正如图5所示，相比使用1000张训练实例，使用50000张训练实例的情况下，测试数据和训练数据的准确率更加接近。特别地，训练数据上最高的分类精度97.86%，仅仅比测试数据的95.53%高出1.53%，而之前有17.73%的差距！

图5. 增大数据量后训练集及测试集随迭代次数的变化情况

虽然过拟合仍然存在，但已经大大降低了。我们的网络能从训练数据更好地泛化到测试数据。一般来说，增加训练数据的数量是降低过拟合的最好方法之一。即便拥有足够的训练数据，要让一个非常庞大的网络过拟合也是比较困难的。不幸的是，训练数据的获取成本太高，因此这通常不是一 个现实的选择。

  因为扩充真实的训练数据是困难的，所以可以认为的扩展训练数据（又称上采样）。如对图像进行小的角度的旋转，除此之外，论文《Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis》 (作者为Patrice Simard，Dave Steinkraus， John Platt , 2003 ）中还转换和扭曲图像来扩展训练数据，甚至提出一种为了模仿手部肌肉的随机抖动的特殊的的图像扭曲方法，这些方法都起到了较好的扩充数据的目的。

  所以一般就是通过应用反映真实世界变化的操作来扩展训练数据，这往往是一个机理模型，一个可以被很好解释的模型。例如要构建一个 神经网络来进行语音识别，甚至可以在有背景噪声的情况下识别语音，即通过增加背景噪声来扩展训练数据，同样能够对其进行加速和减速来获得相应的扩展数据。 所以这是另外的一些扩展训练数据的方法。这些技术并不总是有用~——~例如，其实与其在数据中加入噪声倒不如先对数据进行噪声的清理，这样可能更加有效。

  我们将神经网络与SVM通过实验进行对比，图6是SVM模型和神经网络的性能随着训练数据集的大小变化的情况

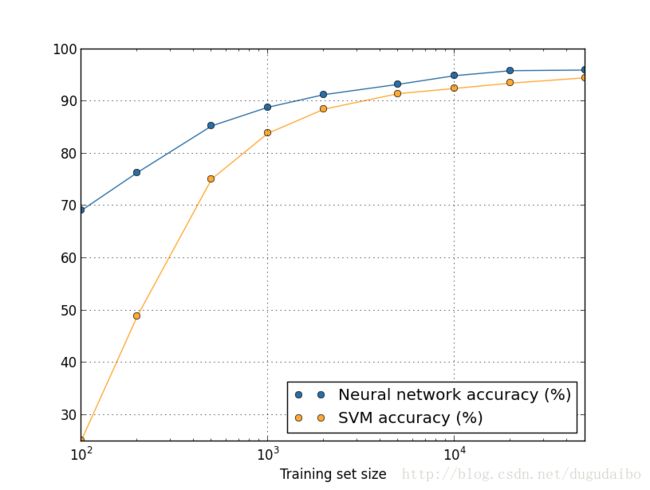
图6 . SVM模型和神经网络的性能随着训练数据集的大小变化的情况

从上面的图像可以发现两条明显的结论，首先神经网络在每个训练规模下性能都超过了SVM；其次更多的训练数据可以补偿不同的机器学习算法的差距。所以需要记住的特别是在实际应用中，我们想要的是更好的算法和更好的训练数据。寻找更好的算法很好，不过需要确保你在此过程中，没有放弃对更多更好的数据的追求。

2.2 减小网络规模

  我们并不情愿减小规模，因为大型网络比小型网络有更大的潜力。

2.3 正则化

  对于固定的网络和固定的训练数据，也有避免过拟合的方法，这就是所谓的正则化（regularization）技术。在本小节将描述4种正则化技术，其中最常见的是权重衰减（weight decay）或叫 L2 正则化（L2 regularization），除此之外还有 L1 正则化、弃权(Dropout)。

2.3.1 L2 正则化

• L2 正则化的定义

  把增加了 L2 正则化项的代价函数写成如等式 (2) 的形式

C=C0+λ2n∑ww2(2)

其中的 C0 是原本的、没有正则化的代价函数，根据之前介绍的这里的代价函数可以是均方误差函数也可以是交叉熵函数。从上面的表达式可以看出，正则化可以视作一种能够折中考虑小权值和最小化原来代价函数的方法。两个要素的相对重要性由 λ 的值决定：当 λ 较小时，我们偏好最小化原本的代价函数，而 λ 较大时我们偏好更小的权值。

• 增加正则化后的梯度下降法

  有了增加正则项的代价函数之后，便需要考虑决如何把随机梯度下降学习算法应用于正则化的神经网络中，即如何对网络中所有的权值和偏移计算偏导数。对等式 (2) 两侧同时求偏导数可得

⎧⎩⎨⎪⎪∂C∂w=∂C0∂w+λnw∂C∂b=∂C0∂b(3)

于是我们发现计算正则化代价函数的梯度相当简单：只要照常使用反向传播，并把 λnw 加到所有权值项的偏导数中。偏移的偏导数保持不变，所以偏移的梯度下降学习的规则保持常规的不变

b→b−η∂C0∂b(4)

而对于权值的学习规则变为：

w→w−η∂C0∂w−λnw=(1−ληn)w−η∂C0∂w(5)

其它部分与常规的梯度下降学习规则完全一样，不一样的地方是我们以 (1−ληn) 调整权值。这种调整有时也被称作权重衰减（weight decay），因为它减小了权重。一眼看去权值将被 不停地减小直到为0。但实际上并不是这样的，因为如果可以减小未正则化的代价函数的话， 式中的另外一项可能会让权值增加。

  对于随机梯度下降方法是类似的，首先在包含 m 个训练样例的 mini-batch 数据中进行平均以估计 ∂C0∂w 的值。 因此对于随机梯度下降法而言正则化的学习方法就变成了

w→(1−ληn)w−ηm∑x∂Cx∂w(6)

其中的求和是对mini-batch中的所有训练样例进行的，是每个样例对应的未正则化的代价。这与通常的随机梯度下降方法一致，除了权重衰减变量 (1−ληn) 。对于偏移的正则化学习规则与未正则化的情况完全一样

b→b−ηm∑x∂Cx∂b(7)

其中的求和是对mini-batch中的所有训练样例 x 进行的。

• 举例说明正则化的作用

  使用一个神经网络来进行验证，其包含30个隐藏神经元，mini-batch大小为10，学习率为0.5，并以交叉熵作为代价函数，设置正则化参数 λ=0.1 。同样首先观察训练集上代价函数随迭代次数的变化情况如图7

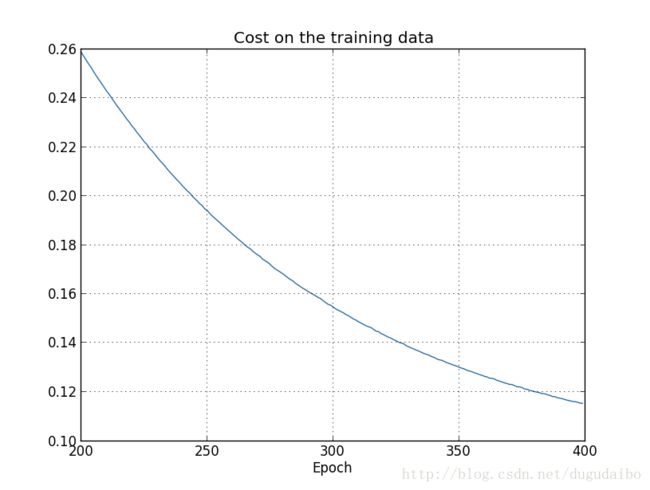
图 7. 增加正则项后训练集上代价函数随迭代次数的变化情况

代价函数一直都在下降，几乎与此前在未正则化的情形一样 。同样观察测试集上代价函数随迭代次数的变化情况如图8

图8 . 增加正则项后测试集上代价函数随迭代次数的变化情况

显然应用正则化抑制了过拟合，同时提升了准确率：分类准确率峰值为87.1%，更高于未正则化例子中的峰值82.27%。实际上，继续进行迭代可以得到更好的结果。从经验来看，正则化让我们的网络分类正确率，并有效地减弱了过拟合效应。

  我们提高训练数据的数量并观察效果，采用50000张图片进行训练，30次迭代，学习率为0.5，minibatch数目为10。然而，我们需要调整正则化参数。因为训练数据集的大小已经从1000变成了50000，根据 (1−ληn) ，如果我们继续使用 λ=0.1 ，那么权重衰减将会大大减小，而正则化的效果也会相应减弱，故调整 λ=5.0 以进行补偿，得到实验结果如图9所示

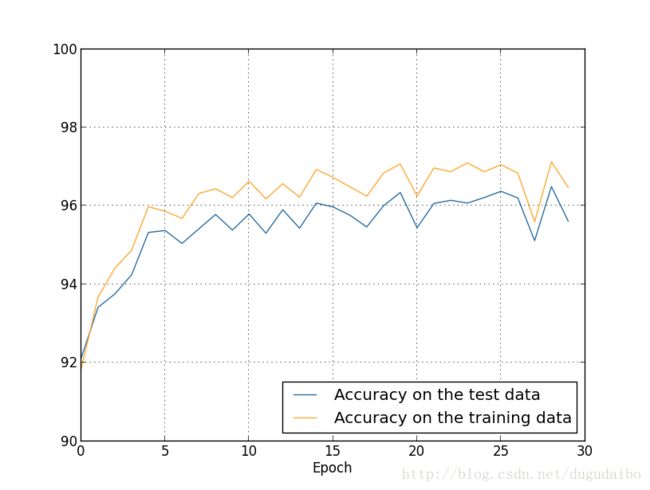
图9 .增加训练数据及正则项后训练集及测试集随迭代次数的变化情况

首先，我们在测试数据上的分类准确率提升了，从未正则化时的95.49%到96.49%，这是一个重大的提升。第二，我们能看到训练数据的结果与测试数据的之间的间隙相比之前也大大缩小了，在一个百分点之下。虽然这仍然是一个明显的间隙，但我们显然已经在减弱过拟合上做出了大量的提升。继续增加神经元个数及迭代次数会使准确率进一步上升。

• 正则化的优点

  正则化的优点主要体现在三个方面，从上面的实验可以明显看出其中两个，即减弱过拟合和提升分类准确率。最后一个优点在于更容易复现结果，因为未正则化的神经网络偶尔会被「卡住」，似乎陷入了代价函数的局部最优中，因此每次运行可能产生相当不同的结果。

2.3.2 L1 正则化

   L1 正则化这个方法是在未正则化的代价函数上加上一个权重绝对值的和，即

C=C_0+\frac{\lambda}{2n}\sum_w|w|\tag{8}\label{8}

它与 L2 正则化相似之处在于惩罚大的权重，倾向于让网络优先选择小的权重。但是它也与 L2 有两点不同。首先在计算偏导数的时候会产生不同，

\frac{\partial C}{\partial w}= \frac{\partial C_0}{\partial w}+\frac{\lambda}{n}sgn(w)\tag{9}\label{9}

其中 sgn() 就是 w 的正负号，正数时为1，负数时为 -1。但是在 w=0 的时候，偏导数 ∂C∂w 未定义，因为在该处倒数是不存在的。所以在 w=0 处应用通常的（无规范化的）随机梯度下降法，因为规范化的效果就是缩小权重，显然不能对一个已经是0的权重进行缩小了。更准确地说，我们约定 sgn(0)=0 。这样就给出了一种细致又紧凑的规则来进行采用 L1 正则化的随机梯度下降学习。

  使用这个表达式，我们可以轻易地对反向传播进行修改从而使用基于 L1 正则化的随机梯度下降进行学习。对 L1 正则化的网络进行更新的规则就是

w\rightarrow w-\frac{\lambda \eta}{n}sgn(w) -\eta\frac{\partial C_0}{\partial w}\tag{10}\label{10}

  第二个不同点在于在 L1 正则化中，权重通过一个常量向0进行缩小;在 L2 正则化中，权重通过一个和 w 成比例的量进行缩小的。所以，当一个特定的权重绝对值很大时， L1 正则化的权重缩小得远比 L2 正则化要小得多。相反，当一个特定的权重绝对值很小时， L1 正则化的权重缩小得要比 L2 正则化大得多。终的结果就是： L1 正则化倾向于聚集网络的权重在相对少量的高重要度连接上，而其他权重就会被驱使向接近，也就是常常提到的 L1 具有稀疏性。

  举个例子，假如有一个权重，它的绝对值相对较大，在更新权重的过程中，因为它的更新速度相对于 L2 正则化的率减速度小，因此可能在较长一段时间内均保持原来较大的值；假如有一个权重，它的绝对值相对较小，在更新权重的过程中，因为它的更新速度相对于 L2 正则化的率减速度大，因此可能在较长一段时间内均保持原来较小的值。这样就可以直观地解释上面提到的稀疏性。

2.3.3 弃权（Dropout）

  弃权（Dropout）是一种相当激进的技术，和 L1 、 L2 正则化不同，弃权技术并不依赖对代价函数的修改，而是在弃权中改变了网络本身。

• Dropout基本的工作机制

  首先会从网络中随机地、临时地删除的一半的隐藏神经元，同时让输入层和输出层的神经元保持不变。在此之后，得到如图 10 所示的网络。

图10 .删除一般隐层神经元后的神经网络

注意那些被弃权的神经元，即临时被删除的神经元在图中用虚圈表示。输入 x ，通过修改后的网络前向传播，然后同样通过这个修改后的网络反向传播结果。在一个minibatch的若干样本上进行这些步骤后，我们对有关的权重和偏置进行更新。然后重复这个过程，首先重置弃权的神经元，然后选择一个新的随机的隐藏神经元的子集进行删除，估计对一个不同的minibatch的梯度，然后更新权重和偏置。因此Dropout是发生在每一次minibatch中的参数更新中，即有一次minibatch的更新，Dropout一次。

  通过不断地重复，网络会在一半的隐藏神经元被弃权的情形下学到一个权重和偏置的集合。因此实际运行整个网络时，是指两倍的隐藏神经元将会被激活。为了补偿这个，我们将把隐藏神经元的权重减半。Alex Krizhevsky 认为这个技术减少了复杂的神经元之间的互适应，因为一个神经元不能够依赖于特定其他神经元的存在。因此，这个就强制性地让我们学习更加健壮的在很多不同的神经元的随机子集的交集中起到作用的那些特征。

• Dropout与正则化的关系

  假设采用相同的数据从不同的初始状态训练几个不同的神经网络，很明显他们是不同的，而且对于一些数据分类结果也有可能是不同的。如果我们训练了五个网络，其中三个把一个数字分类成“3”，那很可能它就是“3”。另外两个可能就犯了错误。这种平均的方式通常是一种强大（尽管代价昂贵）的方式来减轻过度拟合。原因在于不同的网络可能会以不同的方式过度拟合，平均法可能会帮助我们消除那样的过度拟合。启发式地看，当我们弃权掉不同的神经元集合时，有点像我们在训练不同的神经网络。所以，弃权过程就如同大量不同网络的效果的平均那样，从而达到减轻过度拟合的目的。

  如果将我们的神经网络看做一个进行预测的模型的话，我们就可以将弃权看做是一种确保模型对于一部分证据丢失健壮的方式。这样看来，弃权和 L1 、 L2 正则化也是有相似之处的，这也倾向于更小的权重，后让网络对丢失个体连接的场景更加健壮。
  为什么会倾向于更小的权重，不是很懂啊！！！！！！

  感谢“u010312436”的回答。这主要的原因在于如果权重比较小，系统对于外部的偶然的改变或者噪声的反应也就比较小，那么系统就更偏向于经常出现的正确的数据

• Dropout的应用场合

  弃权技术在训练大规模深度网络时尤其有用，这样的网络中过度拟合问题经常特别突出。

3. 为什么正则化可以降低过拟合

  在这一部分，书中并没有给出严格的数学推导及证明，因此本文余下部分也是从实际的经验出发对“为什么正则化可以降低过拟合”这一现象做出定性说明。

  一个大家经常说起的解释是：在某种程度上，越小的权重复杂度越低，因此能够更简单且更有效地描绘数据，所以我们倾向于选择这样的权重。有一种看法是，在科学上，除非迫不得已，我们都应该用更简单的解释。如同样对某一些散点数据进行拟合，基于这种观点，9次模型真的只是学习到了一些局部噪声的影响。因此当9次模型完美拟合了这一特定数据集的时候，这个模型不能很好泛化到其它数据集上，所以包含噪声的线性模型在预测中会有更好的表现。

  将这种观点引申到我们的神经网络中，使用了正则化的神经网络往往具有跟小的权重，小权重意味着网络的行为不会因为我们随意更改了一些输入而改变太多，这使得它不容易学习到数据中局部噪声。可以把它想象成一种能使孤立的数据不会过多影响网络输出的方法，相反地，一个正则化的网络会学习去响应一些经常出现在整个训练集中的实例。与之相对的是，如果输入有一些小的变化，一个拥有大权重的网络会大幅改变其行为来响应变化。因此一个未正则化的网络可以利用大权重来学习得到训练集中包含了大量噪声信息的复杂模型。概括来说，正则化网络能够限制在对训练数据中常见数据构建出相对简单的模型，并且对训练数据中的各种各样的噪声有较好的抵抗能力。所以我们希望它能使我们的网络真正学习到问题中的现象的本质，并且能更好的进行泛化。

  上述的观点十分符合一个一种名叫“奥卡姆剃刀”的想法，但是“奥卡姆剃刀”本身并不是一个普遍成立的科学原理。并不存在一个先验的符合逻辑的理由倾向于简单的模型，而不是复杂的模型。实际上，有时候更复杂的模型反而是正确的。如简单的施恩例子并不存在，复杂的爱因斯坦理论可以解释更多牛顿定理无法解释的现象。因此要从三个方面考虑“简单”这种观点。第一，判断两个解释哪个才是真正的“简单”是一个非常微妙的事情。第二，即便我们能做出这样的判断，简单是一个必须非常谨慎使用的指标。第三，真正测试一个模型的不是简单与否，更重要在于它在预测新的情况时表现如何。

  这三方面的观点主要是为了解释为什么还没有人 研究出一个完全令人信服的理论来解释为什么正则化会帮助网络泛化。正则化可以给我们一个计算魔法棒来帮助我们的网络更好的泛化，但是它并没有给我们一个原则性的 解释泛化是如何工作的，也没有告诉我们最好的方法是什么。

  事实上，我们的网络已先天地泛化得很好。一个具有100个隐层神经元的网络有近80,000个 参数，而我们的训练数据中只有50,000个图像，这就好比试图将一个80,000次多项式拟合为50,000 个数据点。按理来说，我们的网络应该退化得非常严重。然而，正如我们所见，这样一个网络事实上泛化得非常好。为什么会是这样？这不太好理解。据推测说多层网络中的梯度下降学习的过程中有一个『自我正则化』效应。这是非常意外的好处，但是这也某种程度上让人不安，因为我们不知道它是怎么工作的。与此同时，我们将采用一些更务实的方法并尽可能地应用正则化，我们的神经网络将会因此变得更好。

  事实上 L2 正则化没有约束偏置(biases)，在一定程度上，是否正则化偏置仅仅是一个习惯问题。然而值得注意的是，有一个较大的偏置并不会使得神经元对它的输入像有大权重那样敏感。所以我们不用担心较大的偏置会使我们的网络学习训练数据中的噪声。同时，允许大规模的偏置使我们的网络在性能上更为灵活——特别是较大的偏置使得神经元更容易饱和，这通常是我们期望的。由于这些原因，我们通常不对偏置做正则化。