基本概念
“变分自动编码器”(Variational Autoencoders,缩写:VAE)的概念来自Diederik P Kingma和Max Welling的论文《Auto-Encoding Variational Bayes》。现在有了很广泛的应用,应用范围已经远远超出了当时论文的设想。不过看起来似乎,国内还没有见到什么相关产品出现。
作为普及型的文章,介绍“变分自动编码器”,要先从编码说起。
简单说,编码就是数字化,前面第六篇我们已经介绍了一些常见的编码方法。比如对于一句话:“It is easy to be wise after the event.”。使用序列编码的方式,我们可以设定1代表it,2代表is,3代表easy,以此类推,就好像我们机器翻译程序中第一步编码做的那样。图片也是一样,比如我们可以让1代表猫猫的照片,2代表狗狗的照片。
有编码对应就有解码,解码是编码的反过程,比如见到1就还原成“it”,或者还原成一幅猫猫的照片。
这样的编码如此简单,看上去其实根本不需要有什么“自动编码器”存在。
但这些编码是没有“灵魂”的,所谓没有灵魂,就是除非你保留了完整的对照表和原始数据,否则你看到1没办法知道1代表是it,也没办法知道1代表猫猫的照片。甚至即便你知道1代表猫猫,但猫猫图片那么多,究竟是哪张猫猫的照片,你还是不知道。
这个只有智慧生物才具有的“灵魂”,把编码的难度提高了无数倍。
但这是合理的,就比如你见到一只猫猫,你心中会想“这是一只猫”;有人给你说“我刚才见到了一只橘猫”,你脑海中会出现一只卖萌的加菲,也许顺便还在想“十只橘猫九只胖”。这个动作来自于你思维中的长期积累形成的概念化和联想,也实质上相当于编码过程。你心中的“自动编码器”无时不在高效的运转,只不过我们已经习以为常,这个“自动编码器”就是人的智慧。这个“自动编码器”的终极目标就是可能“无中生有”。
上一节神经网络翻译,我们知道这个编码结果实际就是神经网络对于一句话的理解。对于自然语言如此,对于图同样如此。
深度学习技术的发展为自动编码器赋予了“灵魂”,自动编码器迅速的出现了很多。我们早就熟悉的分类算法就属于典型的自动编码器,即便他们一开始表现的并不像在干这个。按照某种规则,把具有相同性质的数据,分配到某一类,产生相同的编码------这就是分类算法干的。不像自动编码器的原因主要是在学习的过程中,我们实际都使用了标注之后的训练集,这个标注本身就是人为分类的过程,这个过程称不上自动。但也有很多分类算法是不需要标注数据的,比如K-means聚类算法。
一个基于深度学习模型的编码器可以轻松的经过训练,把一幅图片转换为一组数据。再通过训练好的模型(你可以理解为存储有信息的模型),完整把编码数据还原到图片。NMT机器翻译,也算的上实现了这个过程。
所以在图片应用中的自动编码器,最终的效果更类似于压缩器或者存储器,把一幅图片的数据量降低。随后解码器把这个过程逆转,从一组小的数据量还原为完整的图片。
变分自动编码器
传统的自动编码器之所以更类似于压缩器或者存储器。在于所生成的数据(编码结果、压缩结果)基本是确定的,而解码后还原的结果,也基本是确定的。这个确定性通常是一种优点,但也往往限制了想像力。
变分自动编码器最初的目的应当也是一样的,算是一种编解码器的实现。最大的特点是首先做了一个预设,就是编码的结果不是某个确认的值,而是一个范围。算法认为编码的结果,根据分类的不同,目标值应当平均分布在一个范围内。这样设计是非常合理的,平均分布在一个范围,才能保证编码空间的利用率最大化并且相近类之间又有良好的区分度。
如何表示一个范围呢?论文中使用了平均值和方差。也就是表示,多幅图片的编码结果值,平均分布在平均值两侧的方差范围内。也可以说符合高斯分布或者正态分布。在本例的程序中(本例中的代码来自TensorFlow官方文档),使用了平均值和对数方差,从数学性能上,对数方差数值会更稳定。基本原理是相同的。
这样一个改变,使得编码结果有了很多有趣的新特征。比如对于编码结果的值进行微调,然后再解码还原之后,生成的图片可能会产生了一些令人兴奋的变化。
从资料介绍的情况看(参考资料),比如对一组人脸照片进行编码,调整编码的某个数值项,结果的人脸肤色可能发生变化;调整另外一个数值,人脸的朝向可能发生了变化。
模型就此似乎获得了令人兴奋的创造能力,而原本这应当是艺术家、人类的领域范围。
另外一个例子中,通过对一组序列的视频图片的学习,随后删去其中的一部分,比如一辆驶过的汽车。然后使用VAE重新生成删除的画面,可以完美再现画面的背景,汽车似乎从未出现在那里。这样的功能,我们在某大公司的图像、视频处理软件中已经见到了商业化的实现(Neural Inpainting)。

程序要点
本示例程序中使用的训练图片,就是手写数字的样本库,这是我们最容易获取到的样本集。
我们希望经过大量的训练之后,VAE模型能够自动的生成可以乱真的手写字符图片。
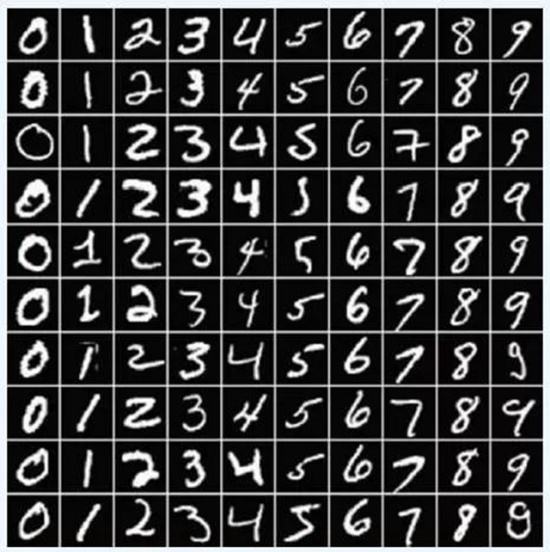
(MNIST手写数字样本图片)
程序一开始,先载入MNIST样本库。根据模型卷积层的需要,将样本整形为样本数量x宽x高x色深的形式。最后把样本规范化为背景色为0、前景笔画为1的张量数据。
程序训练的结果,是使用随机生成的编码向量,还原为手写的数字图片。因为编码是随机生成的,所以不同的编码,生成的图片不可能完全吻合原有的样本集,而这种合理的差异,更类似人自己每次手写的字体------大体上是一致的,但有很多细微的区别。看起来就好像计算机有了人的智慧,在学习了很多手写数字的样本后,自己也能手写数字。

(VAE经过100次训练迭代后,生成的手写数字样本图片)
下面就是随机生成4格x4格共16个样本编码向量,每个向量长度是50个浮点数:
...
latent_dim = 50
num_examples_to_generate = 16
...
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])这一组编码在整个程序中是保持不变的,这样每次生成的图片是相同的一组数字,从而,能观察到从最初生成的一组白噪声,一点点清晰,到第100次迭代的时候较为可以辨别的手写数字。
程序的编码模型(推理模型)和解码模型(生成模型)虽然略微复杂,但在Keras.Sequential的帮助下看上去也没有什么。真正复杂的是程序的代价函数和代价值的计算。
因为模型的代价值是真实图片同生成图片之间的对比,乘上每批次100幅样本图片,是一个比较大的数据量,再考虑编码所使用的范围方式,VAE使用了一个新的计算方法。这部分公式请参考本文开头链接的论文。在程序中,把公式使用代码实现是下面两个函数:
# 计算代价值
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
# 代价函数
def compute_loss(model, x):
# 编码一个批次(100)的图片
mean, logvar = model.encode(x)
# 随机生成100个均匀分布的编码向量
z = model.reparameterize(mean, logvar)
# 使用编码向量生成图片
x_logit = model.decode(z)
# 下面是代价之计算,结构很复杂,但来源是生成图片和样本图片的对比
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)编码向量的长度值是一开始就确定的,本例中是50。这个长度根据需要可以调整,代表了编码所占用的存储空间。编码如果比较长,能包含的图片细节就多,还原的图片容易做到更吻合原图。编码如果短,准确的编码本身一般不会有大的问题,但编码稍有变化,结果的图片变化可能就很大。这相当于等级比例的变化,很容易理解。 每次编码完成后,得到的是平均值和对数方差。是表示范围的量,在本例中,这个范围代表了100副图片的编码。而解码的时候,解码器肯定需要指定具体某幅图片的编码向量值,而不能是一个范围。程序使用下面的函数在指定范围内生成100个编码向量的数组:
# 在向量空间内均匀分布生成100个随机编码
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean再次提醒这里使用的是对数方差,所以跟论文中的公式有区别。
此外注意这里每次生成的100个随机编码,同训练集定义的每个批次100个样本的数量,是必须吻合的。这样生成的图片才是相同的数量,从而同相同数量的样本集对比计算代价值。
程序在训练的每次迭代中都生成一张相同编码值、相同模型、不同阶段(不同模型权重)得出的解码样本图片,保存为文件:
# 产生一幅图片,输出的时候文件名加上迭代次数
def generate_and_save_images(model, epoch, test_input):
# 生成16幅样本图片
predictions = model.sample(test_input)
# 4格*4格图片
fig = plt.figure(figsize=(4, 4))
# for i in range(predictions.shape[0]):
# 用样本中的前16幅生成一张4x4排布的汇总图片
for i in range(4*4):
plt.subplot(4, 4, i+1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# 把生成的图片保存为图片文件
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
# 也可直接显示在屏幕上,但训练过程比较慢,你不一定想等着看
# plt.show()
# 如果图片只是用于保存而非显示,则不会有用户手动“关闭”图片窗口
# plt对象也就无法关闭,所以需要显示的关闭释放内存,特别是本例中图片数量非常多
plt.close()最后一共生成100张图片,如果生成一张gif动图,那看起来会对训练过程的认识格外深刻:
生成动图的程序代码如下,可以单独形成一个程序执行:
#!/usr/bin/env python3
from __future__ import absolute_import, division, print_function, unicode_literals
# 执行前请先安装imageio库
# pip3 install imageio
import os
import time
import numpy as np
import glob
import matplotlib.pyplot as plt
import PIL
import imageio
# 遍历所有png图片,生成一张gif动图
anim_file = 'cvae-100-all.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
last = -1
for i, filename in enumerate(filenames):
frame = 2*(i**0.5)
if round(frame) > round(last):
last = frame
else:
continue
image = imageio.imread(filename)
writer.append_data(image)
# 最后一张图片是最终效果图,多存一张让显示时间长一点
image = imageio.imread(filename)
writer.append_data(image)完整VAE代码
最后是完整的VAE代码,请参考注释阅读:
#!/usr/bin/env python3
# 引入所需库
from __future__ import absolute_import, division, print_function, unicode_literals
import tensorflow as tf
import os
import time
import numpy as np
import glob
import matplotlib.pyplot as plt
# 读取手写字体样本集
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
# 重整为:样本数x宽x高x色深 的格式
train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')
test_images = test_images.reshape(test_images.shape[0], 28, 28, 1).astype('float32')
# 规范化数据到0-1浮点
train_images /= 255.
test_images /= 255.
# 将数据二值化,背景是0,笔画是1
train_images[train_images >= .5] = 1.
train_images[train_images < .5] = 0.
test_images[test_images >= .5] = 1.
test_images[test_images < .5] = 0.
TRAIN_BUF = 60000
BATCH_SIZE = 100
TEST_BUF = 10000
# 这里需要注意一下批次数量是100
train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(TRAIN_BUF).batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.from_tensor_slices(test_images).shuffle(TEST_BUF).batch(BATCH_SIZE)
class CVAE(tf.keras.Model):
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
# 推理模型,相当于Encoder,用于把手写数字图片,编码到向量
# 这里得到的不直接是向量本身,而是向量的均值和对数方差
# 原因看文中的解释
self.inference_net = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# 均值和对数方差的长度都是latent_dim,所以这里是两个
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
# 生成模型,相当于Decoder,使用编码生成对应的手写数字图片
self.generative_net = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64,
kernel_size=3,
strides=(2, 2),
padding="SAME",
activation='relu'),
tf.keras.layers.Conv2DTranspose(
filters=32,
kernel_size=3,
strides=(2, 2),
padding="SAME",
activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=(1, 1), padding="SAME"),
]
)
# 获取一百幅样本图片
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
# 编码器
def encode(self, x):
mean, logvar = tf.split(self.inference_net(x), num_or_size_splits=2, axis=1)
# 每一步都保存一份平均值和对数方差,以便将来你可能想生成一组符合平均分布的编码
self.mean = mean
self.logvar = logvar
return mean, logvar
# 在向量空间内均匀分布生成100个随机编码
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
# tf.exp is e^(logvar*0.5)
return eps * tf.exp(logvar * .5) + mean
# 解码器
def decode(self, z, apply_sigmoid=False):
logits = self.generative_net(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits
optimizer = tf.keras.optimizers.Adam(1e-4)
# 代价值的计算比较复杂,是公式的编程实现
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
# 代价函数
def compute_loss(model, x):
# 编码一个批次(100)的图片
mean, logvar = model.encode(x)
# 随机生成100个均匀分布的编码向量
z = model.reparameterize(mean, logvar)
# 使用编码向量生成图片
x_logit = model.decode(z)
# 下面是代价之计算,结构很复杂,但来源是生成图片和样本图片的对比
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)
# 进行一次训练和梯度迭代
def compute_gradients(model, x):
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
return tape.gradient(loss, model.trainable_variables), loss
# 根据梯度下降计算的结果,调整模型的权重值
def apply_gradients(optimizer, gradients, variables):
optimizer.apply_gradients(zip(gradients, variables))
# 训练迭代100次
epochs = 100
# 编码向量的维度
latent_dim = 50
# 用于生成图片的样本数,4格x4格共16幅
num_examples_to_generate = 16
# 随机生成16个编码向量,在整个程序过程中保持不变,从而可以看到
# 每次迭代,所生成的图片的效果在逐次都在优化。相同的编码会生成相同的目标数字图片
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])
# 模型实例化
model = CVAE(latent_dim)
# 产生一幅图片,输出的时候文件名加上迭代次数
def generate_and_save_images(model, epoch, test_input):
# 生成16幅样本图片
predictions = model.sample(test_input)
# 4格*4格图片
fig = plt.figure(figsize=(4, 4))
# for i in range(predictions.shape[0]):
# 用样本中的前16幅生成一张4x4排布的汇总图片
for i in range(4*4):
plt.subplot(4, 4, i+1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# 把生成的图片保存为图片文件
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
# 也可直接显示在屏幕上,但训练过程比较慢,你不一定想等着看
# plt.show()
# 如果图片只是用于保存而非显示,则不会有用户手动“关闭”图片窗口
# plt对象也就无法关闭,所以需要显示的关闭释放内存,特别是本例中图片数量非常多
plt.close()
# 先生成第一幅、未经训练情况下的样本图片,所有的手写字符都还在随机噪点状态
generate_and_save_images(model, 0, random_vector_for_generation)
# 训练循环
for epoch in range(1, epochs + 1):
start_time = time.time()
for train_x in train_dataset:
# 训练一个批次
gradients, loss = compute_gradients(model, train_x)
apply_gradients(optimizer, gradients, model.trainable_variables)
end_time = time.time()
# 在每个迭代循环生成一张图片和显示一次模型信息
# 可以修改为多次循环显示一次和生成一张图片
if epoch % 1 == 0:
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
loss(compute_loss(model, test_x))
elbo = -loss.result()
# 显示迭代次数、损失值、和本次迭代循环耗时
print("============================")
print(
'Epoch: {}, Test set ELBO: {}, '
'time elapse for current epoch {}'.format(
epoch,
elbo,
end_time - start_time))
# 生成一张图片保存起来
generate_and_save_images(
model, epoch, random_vector_for_generation)最终训练迭代100次后生成的手写数字样本图,虽然已经很有辨识度。但同人写的数字仍然区别很大,原因是,人手写时候误差造成的变形,人类已经看习惯了,几乎不太影响辨别。而机器形成的误差,从人类的眼光中看起来,很怪异,甚至影响识别。这并不能说机器生成的手写字体就不对,至少在机器学习模型看起来,这样的字体已经可以识别了。
我们程序一直使用同一组随机数生成的向量来生成手写字符图片,所以生成的数字一直是同一组。如果程序中再次执行随机生成,得到另外一组随机数,那解码生成的手写图片,也同样会换为另外一组:

当然作为随机数,本身的随意性,所解码还原的图片辨识度,也基本是同样的等级。按照100次的迭代训练来看,也就是比儿童涂鸦略好。
我们开始说过了,VAE的编码目标是平均分配在一个编码空间内的,符合高斯分布。那么我们生成的随机数编码符合这个要求吗?作为50个浮点数长度的向量,这种可能性几乎没有。如果希望得到一个符合正太分布的随机编码向量,需要使用函数reparameterize中提供的方法。比如我们使用这个方法,生成一组编码,再还原为图片看一看:

是不是发现解码还原的图片辨识度高了很多?原因很简单,符合VAE编码规则的编码,所生成的图片,本身就是和训练样本图片最接近、代价值最低的图片。这在人的眼光中看起来好看,实际上,同普通的编码器也就没什么区别了。因为这算不上模型“创造”出来的图片,只是“存储”的图片而已。
所以,VAE之所以受欢迎,就是在于VAE具备了人类才有的创造力,虽然创造的结果不一定都令人满意,但毕竟可以“无中生有”啊。
(待续...)
