机器学习笔记--微积分

本来想直接去学习机器学习的算法的，后来想想还是需要先把基础的数学概念性的看一下，所以决定先从数学知识看起来吧。这里也对微积分做一点基础概念的理解，大学时候的数学也有很多已经遗忘了.这里总结下微积分的一些知识，用作后面的学习。

---

1 极限

设f(x)定义在x0的一个可能不包括x0的区间上，我们说当x趋于x0时，f(x)趋于极限L，并记为：

limx→x0f(x)=L

1.1 三明治(夹逼)定理

假设在包含c在内的某个开区间中除x = c外所有的x，有 g(x)⩽f(x)⩽h(x) ，又假设

limx→cg(x)=limx→ch(x)=L

则

limx→cf(x)=L

简言之就是g(x)和h(x)在x趋向于c的时候的极限为L，那么在中间的那个f(x)的极限也就是L了。
下面举两个例子来求极限：

1.1.1 求sin(x)/x的极限

如图所示
∵sinx<x<tanx
→1<xsinx<1cosx
→cosx<sinxx<1
∵limx→0cosx=cos0=1 ，从而推出:

limx→0sin(x)x=1

1.1.2 求(1+1/n)^n的极限

Xn=(1+1n)n
=1+C1n1n+C2n1n2+C3n1n3+⋯+Cnn1nn
=1+n⋅1n+n(n−1)2!⋅1n2+n(n−1)(n−2)3!⋅1n3+⋯+n(n−1)(n−2)⋯1n!⋅1nn
=1+1+12!⋅(1−1n)+13!⋅(1−1n)(1−2n)+⋯+1n!⋅(1−1n)⋯(1−n−1n)
=1+1+12!+13!+⋯++1n!
<1+1+12+122+⋯++12n−1
=3−12n−1
<3
其实这个极限的值为自然数e。

---

2 导数

2.1 导数的定义

f′(x0)=limΔx→0ΔyΔx=limΔx→0f(x0+Δx)−f(x0)Δx

其实导数就是切线的斜率，是一条曲线变换快慢的反应。

2.2 常用导数

f(x)	f′(x)
C	0
sinx	cosx
xn	nxn−1
ax	axlna
ex	ex
logax	1xlogae
lnx	1x
(u+v)	u′+v′
uv	u′v+uv′

---

3 微分

3.1 微分的定义

函数y=f(x)在某区间有定义， x0 及 x0+Δx 在这区间内，如果函数的增量

Δy=f(x0+Δx)−f(x0)

可表示为

Δy=AΔx+o(Δx)

那么函数y=f(x)在点 x0 可微，而 AΔx 就是微分，记做dy，即：

dy=AΔx

微分是微小的增量，即无穷小量

3.2 微分与导数的关系

通常把自变量x的增量 Δx 称为自变量的微分，记作dx，即 dx=Δx ，于是函数y=f(x)的微分记作

dy=f′(x)dx

从而有：dydx=f′(x)

所以导数也被称作“微商”。可以看如下图，应该更好理解。

---

4 泰勒公式

引用知乎上的一个回答，泰勒公式：就是用多项式函数去逼近光滑函数。

f(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2!(x−x0)2+⋯+fn(x0)n!(x−x0)n+Rn(x)

在计算机中，我们需要求比如 ex 和sinx的话，那么按照计算机的思维，是不知道 ex 和sinx怎么求的。这个时候，用泰勒公式就可以很方便的求出来近似值来了。接着求解下 ex 和sinx的泰勒展开：

ex=1+x+x22!+⋯+xn!+Rn

sinx=x−x33!+x55!−⋯+(−1)m−1x2m−1(2m−1)!+Rn

在近似计算中，可以有如下公式：

0	1
1+x−−−−−√n≈1+1nx	sinx≈x
tanx≈x	ex≈1+x
ln(1+x)≈x	1−x1+x−−−√≈1−x

---

5 方程近似解

5.1 二分法

设f(x)在区间[a, b]上连续， f(a)⋅f(b)<0 且方程f(x)=0在(a, b)内仅有一个实根，然后，每次把区间缩小一半，具体选择左半区还是右半区的原则是使得方程异号。循环该过程，区间的中间点不断逼近方程的根。

如下图可以形象的表示出来，首先取[a1,b1]，然后[a1,b2]，接着[a2, b2], 接着[a3, b2]，依次类推，慢慢接近f(x) = 0，最后求出近似解，这个和循环的次数相关。

5.2 牛顿法

首先，选择一个接近函数f(x)零点的x0，计算相应的f(x0)和切线斜率f’(x0)。然后我们计算穿过点(x0,f(x0))并且斜率为f’(x0)的直线和x轴的交点的x坐标，也就是求如下方程的解：

x⋅f′(x0)+f(x0)−x0⋅f′(x0)=0

化简得到：

xn+1=xn−f(xn)f′(xn)

其实原理是利用泰勒公式, 在 x0 处展开, 且展开到一阶, 即 f(x)=f(x0)+(x–x0)f'(x0) , 化简后就是上述公式了。
可以观察如下图所示，首先是A点，求到B点，接着C点，依次类推，最后到f(x)=0，求出近似值。

---

6 积分

6.1 不定积分的定义

如果区间I上，可导函数F(x)的导函数为f(x)，即对任一 x∈I ,都有

F′(x)=f(x)或者dF(x)=f(x)dx

那么函数F(x)就称为f(x)在区间I上的原函数。
不定积分可以记作：

F(x)=∫f(x)dx

6.2 常用不定积分

0
∫kdx=kx+C	∫xμdx=xμ+1μ+1+C
∫dxx=ln|x|+C	∫dx1+x2=arctanx+C
∫dx1−x2√=arcsinx+C	∫cosxdx=sinx+C
∫sinxdx=−cosx+C	∫dxcos2x=∫sec2xdx=tanx+C
∫dxsin2x=∫csc2xdx=−cotx+C	∫secxtanxdx=secx+C
∫cscxcotxdx=−cscx+C	∫exdx=ex+C
∫axdx=axlna+C	∫shxdx=chx+C
∫chxdx=shx+C
分部积分： uv′=uv−u′v	分部积分： ∫udv=uv−∫vdu

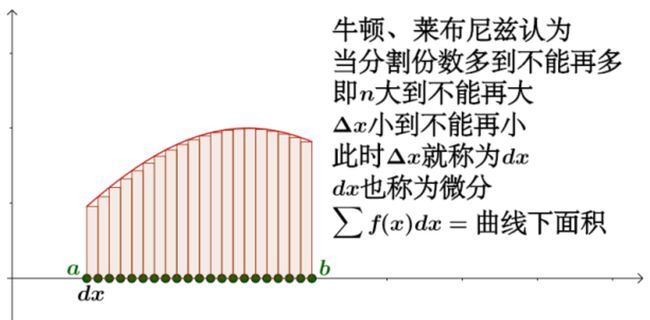
6.3 定积分

如下图所示：

故，记做 ∫baf(x)=∑(fx)dx ，所以定积分在最初定义的时候，就是被定义成面积的。 牛顿-莱布尼兹公式： 如果函数 F(x)是连续函数 f(x)在区间 [a,b]上的一个原函数，那么

∫baf(x)=F(b)−F(a)

***

7 偏导数

7.1 偏导数的定义

• 对于x的偏导
  
  ∂f∂x∣(x0,y0)=ddxf(x,y0)∣(x0,y0)=limh→0f(x0+h,y0)−f(x0,y0)h
• 对于y的偏导
  
  ∂f∂y∣(x0,y0)=ddxf(x0,y)∣(x0,y0)=limh→0f(x,y0+h)−f(x0,y0)h

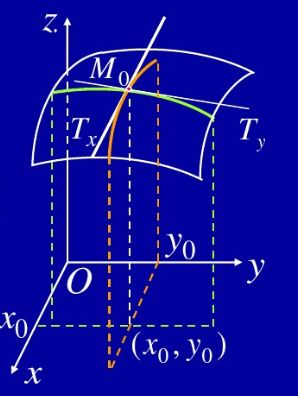
7.2 偏导数的几何意义

如图所示，x的偏导就是曲线

{z=f(x,y)y=y0

在点 M0 处的切线 M0Tx 对x轴方向的斜率。 同理，对y的偏导就是 M0Ty 对y轴方向的斜率。 ***

8 方向导数和梯度

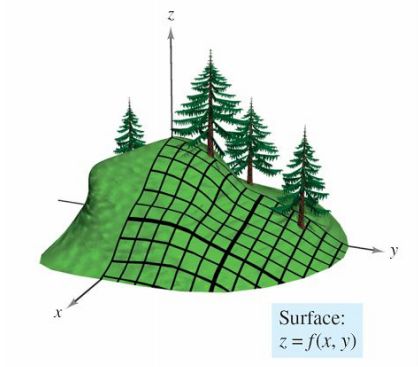
8.1 方向导数定义

假设山坡表示为z=f(x,y)，根据偏导的定义，我们已经知道了y方向的斜率可以对y偏微分得到，同样的，x方向的斜率也可以对x偏微分得到。那如果求任何一切方向的呢，接着就引出了方向导数， 设 f(x,y) 为一个二元函数， u=cosθi+sinθj 为一个单位向量，如果下列的极限值存在:

limt→0f(x0+tcosθ,y0+tsinθ)−f(x0,y0)t

此方向导数记为 Duf

8.2 梯度向量(梯度)定义

f(x,y) 在点 P0 的梯度向量是由求 f 在 P0 的偏导数的值得到的向量：

▽f=fx(x,y)i+fy(x,y)j

方向导数是 f 在 P0 的梯度和u的点积。

Duf=(▽f)P0⋅u=|(▽f)||u|cosθ=|(▽f)|cosθ

由上式可知，因为 cosθ 永远不大于1，所以梯度 ▽f 是方向导数中取到最大值的方向，梯度的值是方向导数的最大值。

---

9 雅可比，海森矩阵

9.1 雅可比矩阵定义

雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近. 因此, 雅可比矩阵类似于多元函数的导数.

假设 F:Rn→Rm 是一个从欧式n维空间转换到欧式m维空间的函数. 这个函数由m个实函数组成: y1(x1,…,xn),…,ym(x1,…,xn) .这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵, 这就是所谓的雅可比矩阵：

⎡⎣⎢⎢⎢⎢⎢⎢⎢∂y1∂x1⋯∂ym∂x1⋯⋱⋯∂y1∂xn⋯∂ym∂xn⎤⎦⎥⎥⎥⎥⎥⎥⎥

此矩阵表示为: JF(x1,⋯,xn) , 或者 ∂(y1,⋯,ym)∂(x1,⋯,xn)
雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近。因此，雅可比矩阵类似于多元函数的导数。雅可比矩阵定义为向量对向量的微分矩阵。

9.2 雅可比行列式

如果m = n, 那么 F 是从n维空间到n维空间的函数, 且它的雅可比矩阵是一个方块矩阵. 于是我们可以取它的行列式, 称为雅可比行列式.

9.3 海森矩阵

在数学中, 海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵, 此函数如下：

f(x1,x2…,xn)

如果 f 的所有二阶导数都存在, 那么 f 的海森矩阵即：

H(f)ij(x)=DiDjf(x)

其中 x=(x1,x2…,xn) , 即 H(f) 为:

⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂2f∂x21∂2f∂x2∂x1⋮∂2f∂xn∂x1∂2f∂x1∂x2∂2f∂x22⋮∂2f∂xn∂x2⋯⋯⋱⋯∂2f∂x1∂xn∂2f∂x2∂xn⋮∂2f∂x2n⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥

可以参考下： Jacobian矩阵和Hessian矩阵

---

10 拉格朗日乘子法

10.1 定义

假设 f(x,y,z) 和 g(x,y,z) 是可微的，求为 f 在约束 g(x,y,z)=0 下的局部最大值和最小最小值，就求 x,y,z 和 λ 的值，使它们同时满足

▽f=λ▽g和g(x,y,z)=0

对于两个变量的函数，适当的方程是

▽f=λ▽g和g(x,y)=0

10.2 例子

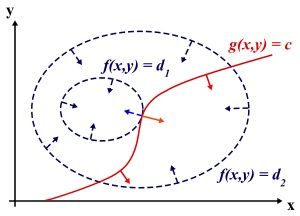
设想我们的目标函数 z=f(x) , x 是向量, z 取不同的值，相当于可以投影在 x 构成的平面（曲面）上，即成为等高线，如下图，目标函数是 f(x,y) ，这里 x 是标量，虚线是等高线，现在假设我们的约束 g(x)=0 ， x 是向量，在 x 构成的平面或者曲面上是一条曲线，假设 g(x) 与等高线相交，交点就是同时满足等式约束条件和目标函数的可行域的值，但肯定不是最优值，因为相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部，使得新的等高线与目标函数的交点的值更大或者更小，只有到等高线与目标函数的曲线相切的时候，可能取得最优值，如下图所示，即等高线和目标函数的曲线在该点的法向量必须有相同方向，所以最优值必须满足： f(x) 的梯度 = λ∗g(x) 的梯度， λ 是常数，表示左右两边同向。这个等式就是 L(λ,x) 对参数求导的结果。

可参考：[深入理解拉格朗日乘子法（Lagrange Multiplier) 和KKT条件](http://blog.csdn.net/xianlingmao/article/details/7919597) ***

11 最小二乘法

11.1定义

• 最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。—-来自百度百科
• 简单地说，最小二乘的思想就是要使得观测点和估计点的距离的平方和达到最小.这里的“二乘”指的是用平方来度量观测点与估计点的远近（在古汉语中“平方”称为“二乘”），“最小”指的是参数的估计值要保证各个观测点与估计点的距离的平方和达到最小。

11.2 例子

设拟合直线是 y=a+bx ,距离（或误差）为 di=yi−(a+bx) ，那么最小二乘的思想就是让等式

Di=∑i=1nd2i=∑i=1n(yi−a−bxi)2

具有最小值。那么这就需要做求偏导了。大致推导过程如下：

∂Di∂a=∑i=1n2(yi−a−bxi)(−1)=−2∑i=1n(yi−a−bxi)

∂Di∂b=∑i=1n2(yi−a−bxi)(−xi)=−2∑i=1n(xiyi−axi−bx2i)

令导数为0整理可得：

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪∑i=1nxiyi−a∑i=1nxi−b∑i=1nx2i=0∑i=1nyi−na−b∑i=1nxi=0

令

nx¯=∑i=1nxi,ny¯=∑i=1nyi

解得：

⎧⎩⎨⎪⎪b=xy¯−x¯y¯x2¯−(x¯)2a=y¯−bx¯

---

还有重积分，向量的导数等等知识点以后学到了再去看吧，突然发现大学的时候只记得公式，具体的为什么很多都不是很清楚，还有很多的几何意义也似懂非懂，慢慢再补吧，继续补下去感觉出不来了。接下来开始看线性代数吧。

---

附上: 希腊字母表(配读音)

序号	大写	小写	English	发音	中文	含义
1	Α	α	alpha	a:lf	阿尔法
2	Β	β	beta	bet	贝塔
3	Γ	γ	gamma	ga:m	伽马
4	Δ	δ	delta	delt	德尔塔	δ: delta value，偏差值
5	Ε	ε	epsilon	ep’silon	伊普西龙
6	Ζ	ζ	zeta	zat	截塔
7	Η	η	eta	eit	艾塔
8	Θ	θ	thet	θit	西塔
9	Ι	ι	iot	aiot	约塔
10	Κ	κ	kappa	kap	卡帕
11	∧	λ	lambda	lambd	兰布达
12	Μ	μ	mu	mju	缪
13	Ν	ν	nu	nju	纽
14	Ξ	ξ	xi	ksi	克西	ξ: slack variable，松弛变量
15	Ο	ο	omicron	omik’ron	奥密克戎
16	∏	π	pi	pai	派	π: 圆周率
17	Ρ	ρ	rho	rou	肉
18	∑	σ	sigma	‘sigma	西格马
19	Τ	τ	tau	tau	套
20	Υ	υ	upsilon	jup’silon	宇普西龙
21	Φ	φ	phi	fai	佛爱
22	Χ	χ	chi	phai	凯
23	Ψ	ψ	psi	psai	普西
24	Ω	ω	omega	o’miga	欧米伽