【python数据挖掘课程】十八.线性回归及多项式回归分析四个案例分享
1.线性回归预测Pizza价格案例
2.线性回归分析波士顿房价案例
3.随机数据集一元线性回归分析和三维回归分析案例
4.Pizza数据集一元线性回归和多元线性回归分析
本篇文章为初始篇,基础文章希望对你有所帮助,如果文章中存在错误或不足支持,还请海涵~自己真的太忙了,只能挤午休或深夜的时间学习新知识,但也得加油。
前文参考:
【Python数据挖掘课程】一.安装Python及爬虫入门介绍
【Python数据挖掘课程】二.Kmeans聚类数据分析及Anaconda介绍
【Python数据挖掘课程】三.Kmeans聚类代码实现、作业及优化
【Python数据挖掘课程】四.决策树DTC数据分析及鸢尾数据集分析
【Python数据挖掘课程】五.线性回归知识及预测糖尿病实例
【Python数据挖掘课程】六.Numpy、Pandas和Matplotlib包基础知识
【Python数据挖掘课程】七.PCA降维操作及subplot子图绘制
【Python数据挖掘课程】八.关联规则挖掘及Apriori实现购物推荐
【Python数据挖掘课程】九.回归模型LinearRegression简单分析氧化物数据
【python数据挖掘课程】十.Pandas、Matplotlib、PCA绘图实用代码补充
【python数据挖掘课程】十一.Pandas、Matplotlib结合SQL语句可视化分析
【python数据挖掘课程】十二.Pandas、Matplotlib结合SQL语句对比图分析
【python数据挖掘课程】十三.WordCloud词云配置过程及词频分析
【python数据挖掘课程】十四.Scipy调用curve_fit实现曲线拟合
【python数据挖掘课程】十五.Matplotlib调用imshow()函数绘制热图
【python数据挖掘课程】十六.逻辑回归LogisticRegression分析鸢尾花数据
【python数据挖掘课程】十七.社交网络Networkx库分析人物关系(初识篇)
一. 线性回归预测Pizza价格案例
1.数据集介绍
本章主要使用线性回归预测Pizza的价格,由于直径大小不同的Pizza,其价格也是不同的。这是一个非常经典的案例,主要包括两个特征——Pizza直径(单位:英寸)和Pizza价格(单位:美元)。假设读者现在去到一家西餐厅,看到Pizza的菜单,现在需要通过机器学习的方法构造一个一元线性回归模型,通过分析匹萨的直径与价格的数据的线性关系,来预测任意直径匹萨的价格。 数据集共十行,包括两个特征,如下表10.1所示。
2.线性回归分析
线性回归基础步骤主要包括:
1.导入数据集,采用列表的形式定义直接和价格两列数据。
2.调用Scikit-learn机器学习包中线性回归模型。
3.调用fit()函数对直径和价格进行训练。
4.调用predice()函数对数据集进行预测。
5.对线性回归算法进行评价。
6.可视化分析并绘制相关图形,直观的呈现算法模型的结果。
线性回归分析的完整代码如下:
# -*- coding: utf-8 -*-
from sklearn.linear_model import LinearRegression
#数据集 直径、价格
x = [[5],[6],[7],[8],[10],[11],[13],[14],[16],[18]]
y = [[6],[7.5],[8.6],[9],[12],[13.6],[15.8],[18.5],[19.2],[20]]
print x
print y
clf = LinearRegression()
clf.fit(x,y)
pre = clf.predict([12])[0]
print(u'预测直径为12英寸的价格: $%.2f' % pre)通过调用sklearn机器学习包中linear_model子类的LinearRegression线性回归模型,然后fit()函数用来分析模型参数,predict()通过fit()算出模型参数构成的模型,对解释变量进行预测获得其结果。上面的代码输出如下所示:
[[5], [6], [7], [8], [10], [11], [13], [14], [16], [18]]
[[6], [7.5], [8.6], [9], [12], [13.6], [15.8], [18.5], [19.2], [20]]
预测直径为12英寸的价格: $14.42可以发现直径为12英寸的Pizza价格为14.42美元。同时它生成了一个一元线性回归模型,即:y = a*x + b。其中,y表示响应变量的预测值,这个示例为Pizza的价格预测值;x为因变量,表示Pizza的直径。
3.可视化分析
接下来需要对数据集进行可视化分析,首先需要调用Matplotlib扩展包绘制直径和价格的散点图,代码如下:
# -*- coding: utf-8 -*-
from sklearn.linear_model import LinearRegression
#数据集 直径、价格
x = [[5],[6],[7],[8],[10],[11],[13],[14],[16],[18]]
y = [[6],[7.5],[8.6],[9],[12],[13.6],[15.8],[18.5],[19.2],[20]]
print x
print y
clf = LinearRegression()
clf.fit(x,y)
pre = clf.predict([12])[0]
print(u'预测直径为12英寸的价格: $%.2f' % pre)
x2 = [[0],[12],[15],[25]]
y2 = clf.predict(x2)
import matplotlib.pyplot as plt
plt.figure()
plt.rcParams['font.sans-serif'] = ['SimHei'] #指定默认字体
plt.title(u"线性回归预测Pizza直径和价格")
plt.xlabel(u"x")
plt.ylabel(u"price")
plt.axis([0,25,0,25])
plt.scatter(x,y,marker="s",s=20)
plt.plot(x2,y2,"g-")
plt.show()输出图形如下所示,其中(x2,y2)是训练后的回归模型进行预测的结果,为一条直线。
二. 线性回归分析波士顿房价案例
1.数据集
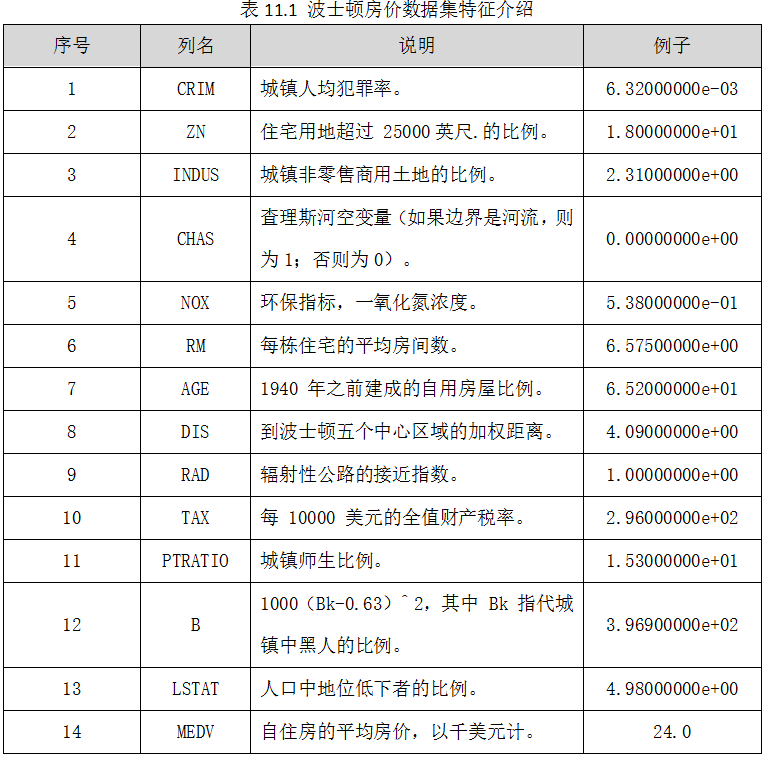
波士顿房价数据集(Boston House Price Dataset)包含对房价的预测(以千美元计数),给定的条件是房屋及其相邻房屋的详细信息。该数据集涉及一个回归问题,通过进行线性回归分析可以预测波斯顿房价数据。而且由于Sklearn机器学习包中已经自带了该数据集,故直接引用该数据集,获取其中某两列数据,对其进行分析预测。
该数据集的下载地址为:http://lib.stat.cmu.edu/datasets/boston,也可以从UCI机器学习知识库中下载,每个类的观察值数量是均等的,共有 506 行数据,13 个输入变量和1个输出变量,数据集如下图11.1所示,这些数据从1978年开始统计,涵盖了波士顿不同郊区房屋14中特征信息。
在做数据分析过程中,通常需要将数据集划分为训练集和预测集,这里作者将前406行作为训练集,最后100行作为预测集,划分代码如下:
# -*- coding: utf-8 -*-
#导入数据集boston
from sklearn.datasets import load_boston
import numpy as np
boston = load_boston()
print boston.data.shape, boston.target.shape
print boston.data[0]
print boston.target
#划分数据集
boston_temp = boston.data[:, np.newaxis, 5]
x_train = boston_temp[:-100] #训练样本
x_test = boston_temp[-100:] #测试样本 后100行
y_train = boston.target[:-100] #训练标记
y_test = boston.target[-100:] #预测对比标记2.线性回归分析
线性回归过程主要如下:
1.导入数据集,波士顿房价数据。
2.划分数据集为训练集和测试集,采用406和100的比例。
3.导入线性回归模型LinearRegression。
4.对训练集进行训练操作,同时预测数据集结果。
5.可视化画图分析及结果评估。
线性回归分析波士顿房价数据集的代码如下:
# -*- coding: utf-8 -*-
from sklearn.datasets import load_boston
import numpy as np
boston = load_boston()
print boston.data.shape, boston.target.shape
#划分数据集
boston_temp = boston.data[:, np.newaxis, 5]
x_train = boston_temp[:-100] #训练样本
x_test = boston_temp[-100:] #测试样本 后100行
y_train = boston.target[:-100] #训练标记
y_test = boston.target[-100:] #预测对比标记
#回归分析
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
clf.fit(x_train, y_train)
#算法评估
pre = clf.predict(x_test)
print u"预测结果", pre
print u"真实结果", y_test
cost = np.mean(y_test-pre)**2
print u'平方和计算:', cost
print u'系数', clf.coef_
print u'截距', clf.intercept_
print u'方差', clf.score(x_test, y_test)
#绘图分析
import matplotlib.pyplot as plt
plt.title(u'LinearRegression Boston')
plt.xlabel(u'x')
plt.ylabel(u'price')
plt.scatter(x_test, y_test, color = 'black')
plt.plot(x_test, clf.predict(x_test), color='blue', linewidth = 3)
for idx, m in enumerate(x_test):
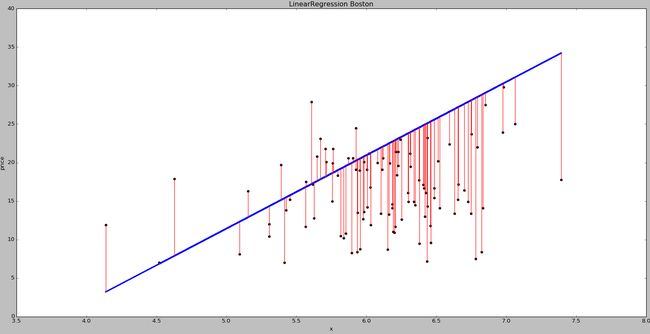
plt.plot([m, m],[y_test[idx],pre[idx]], 'r-')
plt.show() 对该算法进行评估,线性回归算法可以计算线性方程的系数和截距,即coef_为系数、intercept_为截距。同时可以通过clf.score(x_test,y_test)计算其方差。
平方和计算: 32.6621132918
系数 [ 9.52462596]
截距 -36.1965235122
方差 -1.83449598504 三. 随机数据集线性回归分析和三维回归分析案例
1.随机数据集
本章将生成一个随机数据集供您使用,通过该数据集的线性回归分析,您也能了解到相关应用知识。同时,将进一步深入讲解线性回归拟合方程的知识,希望本章对您有所帮助。
随机数生成主要调用Numpy扩展包中的random函数或arange,调用函数arange(0,50,0.2)实现,随机生成0到50个数据,其间隔为0.2。得到X数据集之后,作者随机定义一个函数绘制对应的Y坐标,再调用Matplotlib扩展包可以对数据集进行可视化分析,并绘制相关的散点图。核心代码如下:
import numpy as np
import math
X = np.arange(0,50,0.2)
print X
xArr = []
yArr = []
for n in X:
xArr.append(n)
y = 0.7*n + np.random.uniform(0,1)*math.sin(n)*2 - 3
yArr.append(y)
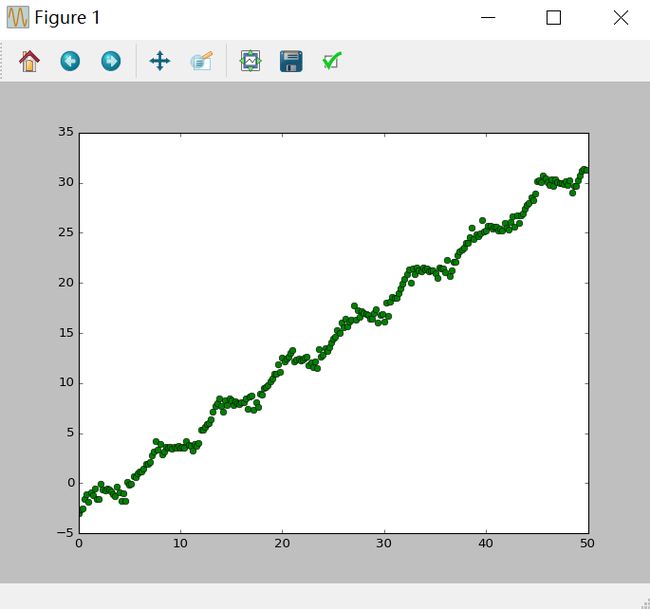
import matplotlib.pyplot as plt
plt.plot(X, yArr, 'go')
plt.show()接下来需要调用Sklearn机器学习扩展包相关函数进行线性回归分析。
2.线性回归
完整代码如下:
# -*- coding: utf-8 -*-
import numpy as np
import math
#随机数生成
X = np.arange(0,50,0.2)
print X
xArr = []
yArr = []
for n in X:
xArr.append(n)
y = 0.7*n + np.random.uniform(0,1)*math.sin(n)*2 - 3
yArr.append(y)
#线性回归分析
from sklearn.linear_model import LinearRegression
clf = LinearRegression()
print clf
X = np.array(X).reshape((len(X),1)) #list转化为数组
yArr = np.array(yArr).reshape((len(X),1))
clf.fit(X,yArr)
pre = clf.predict(X)
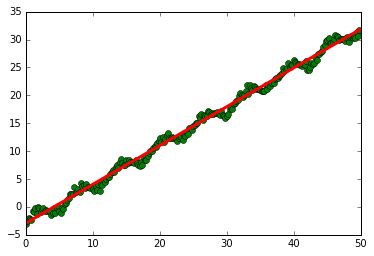
import matplotlib.pyplot as plt
plt.plot(X, yArr, 'go')
plt.plot(X, pre, 'r', linewidth=3)
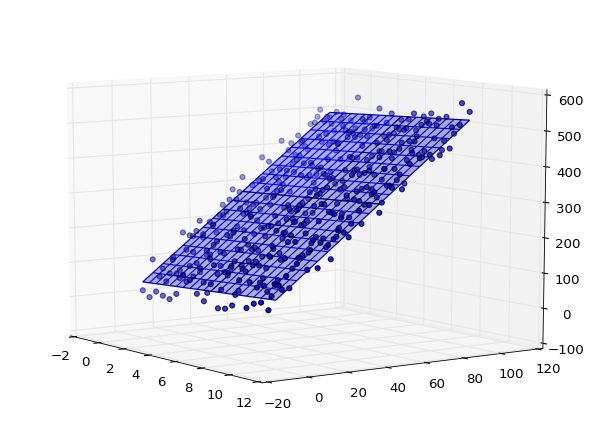
plt.show()同时补充一段3D绘制的代码,随机坐标生成后,需要调用mpl_toolkits.mplot3d子类中Axes3D类生成对应的3D图形。使用线性回归对其进行分析过程中,不同于二维可视化分析,三维需要将xx和yy标定成输入变量,zz为输出变量进行训练,再预测其结果。完整代码如下所示:
# -*- coding: utf-8 -*-
import numpy as np
from sklearn import linear_model
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import math
#linspace:开始值、终值和元素个数创建表示等差数列的一维数组
xx, yy = np.meshgrid(np.linspace(0,10,20), np.linspace(0,100,20))
zz = 2.4 * xx + 4.5 * yy + np.random.randint(0,100,(20,20))
#构建成特征、值的形式
X, Z = np.column_stack((xx.flatten(),yy.flatten())), zz.flatten()
#线性回归分析
regr = linear_model.LinearRegression()
regr.fit(X, Z)
#预测的一个特征
x_test = np.array([[15.7, 91.6]])
print regr.predict(x_test)
#画图可视化分析
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.scatter(xx, yy, zz) #真实点
#拟合的平面
ax.plot_wireframe(xx, yy, regr.predict(X).reshape(20,20))
ax.plot_surface(xx, yy, regr.predict(X).reshape(20,20), alpha=0.3)
plt.show()四. Pizza数据集一元和多元线性回归分析
完整代码如下:
# -*- coding: utf-8 -*-
"""
Created on Sun Nov 26 23:31:16 2017
@author: yxz15
"""
# -*- coding: utf-8 -*-
from sklearn.linear_model import LinearRegression
#数据集 直径、价格
x = [[5],[6],[7],[8],[10],[11],[13],[14],[16],[18]]
y = [[6],[7.5],[8.6],[9],[12],[13.6],[15.8],[18.5],[19.2],[20]]
print x
print y
clf = LinearRegression()
clf.fit(x,y)
pre = clf.predict([12])[0]
print(u'预测直径为12英寸的价格: $%.2f' % pre)
x2 = [[0],[12],[15],[25]]
y2 = clf.predict(x2)
import matplotlib.pyplot as plt
import numpy as np
plt.figure()
plt.axis([0,25,0,25])
plt.scatter(x,y,marker="s",s=20)
plt.plot(x2,y2,"g-")
#导入多项式回归模型
from sklearn.preprocessing import PolynomialFeatures
xx = np.linspace(0,25,100) #0到25等差数列
quadratic_featurizer = PolynomialFeatures(degree = 2) #实例化一个二次多项式
x_train_quadratic = quadratic_featurizer.fit_transform(x) #用二次多项式多样本x做变换
X_test_quadratic = quadratic_featurizer.transform(x2)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(x_train_quadratic, y)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))# 把训练好X值的多项式特征实例应用到一系列点上,形成矩阵
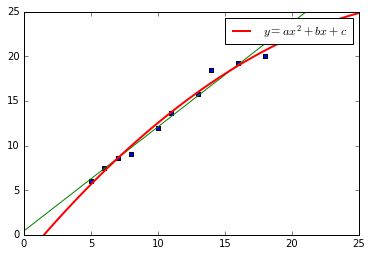
plt.plot(xx, regressor_quadratic.predict(xx_quadratic),
label="$y = ax^2 + bx + c$",linewidth=2,color="r")
plt.legend()
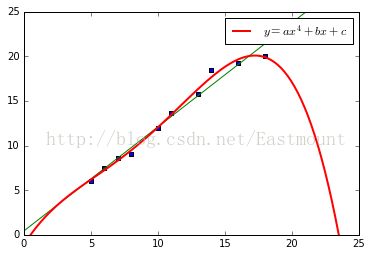
plt.show()四次方拟合,核心代码如下:
#导入多项式回归模型
from sklearn.preprocessing import PolynomialFeatures
xx = np.linspace(0,25,100) #0到25等差数列
quadratic_featurizer = PolynomialFeatures(degree = 4) #实例化一个二次多项式
x_train_quadratic = quadratic_featurizer.fit_transform(x) #用二次多项式多样本x做变换
X_test_quadratic = quadratic_featurizer.transform(x2)
regressor_quadratic = LinearRegression()
regressor_quadratic.fit(x_train_quadratic, y)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))# 把训练好X值的多项式特征实例应用到一系列点上,形成矩阵
plt.plot(xx, regressor_quadratic.predict(xx_quadratic),
label="$y = ax^4 + bx + c$",linewidth=2,color="r")
plt.legend()
plt.show()希望文章对你有所帮助,尤其是我的学生,如果文章中存在错误或不足之处,还请海涵。给绿幺准备惊喜中~
(By:Eastmount 2017-11-26 深夜12点 http://blog.csdn.net/eastmount/ )