【python数据挖掘课程】二十三.时间序列金融数据预测及Pandas库详解
这是《Python数据挖掘课程》系列文章,也是我上课内容及书籍中的一个案例。本文主要讲述时间序列算法原理,Pandas扩展包基本用法以及Python调用statsmodels库的时间序列算法。由于作者数学比较薄弱,自己也还在学习,所以原理推导部分本文只简单叙述,同时参考了《Python金融大数据分析 ·Yves Hilpisch》书籍和其他大神的文章。
本篇文章为基础性文章,希望对你有所帮助,提供些思路,也是自己教学的内容。如果文章中存在错误或不足之处,还请海涵。同时,推荐大家阅读我以前的文章了解其他知识。
前文参考:
【Python数据挖掘课程】一.安装Python及爬虫入门介绍
【Python数据挖掘课程】二.Kmeans聚类数据分析及Anaconda介绍
【Python数据挖掘课程】三.Kmeans聚类代码实现、作业及优化
【Python数据挖掘课程】四.决策树DTC数据分析及鸢尾数据集分析
【Python数据挖掘课程】五.线性回归知识及预测糖尿病实例
【Python数据挖掘课程】六.Numpy、Pandas和Matplotlib包基础知识
【Python数据挖掘课程】七.PCA降维操作及subplot子图绘制
【Python数据挖掘课程】八.关联规则挖掘及Apriori实现购物推荐
【Python数据挖掘课程】九.回归模型LinearRegression简单分析氧化物数据
【python数据挖掘课程】十.Pandas、Matplotlib、PCA绘图实用代码补充
【python数据挖掘课程】十一.Pandas、Matplotlib结合SQL语句可视化分析
【python数据挖掘课程】十二.Pandas、Matplotlib结合SQL语句对比图分析
【python数据挖掘课程】十三.WordCloud词云配置过程及词频分析
【python数据挖掘课程】十四.Scipy调用curve_fit实现曲线拟合
【python数据挖掘课程】十五.Matplotlib调用imshow()函数绘制热图
【python数据挖掘课程】十六.逻辑回归LogisticRegression分析鸢尾花数据
【python数据挖掘课程】十七.社交网络Networkx库分析人物关系(初识篇)
【python数据挖掘课程】十八.线性回归及多项式回归分析四个案例分享
【python数据挖掘课程】十九.鸢尾花数据集可视化、线性回归、决策树花样分析
【python数据挖掘课程】二十.KNN最近邻分类算法分析详解及平衡秤TXT数据集读取
【python数据挖掘课程】二十一.朴素贝叶斯分类器详解及中文文本舆情分析
【python数据挖掘课程】二十二.Basemap地图包安装入门及基础知识讲解
一. 时间序列基础知识
社会经济现象总是随着时间的推移而变迁,呈现动态性。一个或一组变量x(t)进行观测,将在一系列时刻t1、t2、...、tn得到离散数字组成的序列集合,称之为时间序列。通过时间序列算法,我们对事物进行动态的研究。
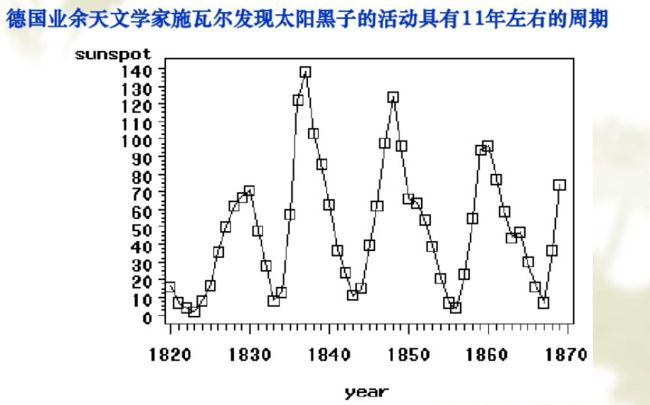
时间序列表示按时间先后顺序排列的数列,通常X轴为时间要素,Y轴为数据要素,比如1986-2000年的人均GDP为y1、y2、...、yn,再如下图所示太阳黑子运动规律。
指标通常包括时期指标(年度、月度)和时点指标(时刻)。时间序列分为以下三类:
1.随机性时间序列:各指标变动受随机因素影响
2.平稳时间序列:基本稳定在某个水平附近波动
3.非平稳时间序列:存在某种规律性变动,比如趋势性、季节性
时间序列常用的特征统计量如下所示:(参考:百度文库)
二. 金融时间序列-Pandas库
该部分是作者学习《Python金融大数据分析》书籍第6章的内容,仅供大家学习:
金融学中最重要的数据类型之一是金融时间序列,以日期时间作为索引的数据,例如股票、GDP、汇率等。Python处理时间序列主要使用Pandas库,其DataFrame和Series等基本类灵感来源于R语言。Pandas库允许从Web上读取数据,比如雅虎财经、谷歌财经等,也可以读取csv文件(逗号分割)。下面详细介绍Pandas库的用法:
1.DataFrame类
首先我们通过DataFrame定义数据,包括数据、标签和索引三部分,其中数据包括列表、元组、字典、ndarray等类型,索引包括数值、字符串和时间等。示例代码如下:
import pandas as pd
import numpy as np
df = pd.DataFrame([10,20,30,40],columns=['num'],
index=['a','b','c','d'])
print df.index
print df.columns
print df.ix['c']
print df.ix[df.index[1:3]]
print df.sum()
print df.apply(lambda x:x**2)输出结果如下所示,包括输出索引、标签值,获取“c”对应数值等,通过df.sum()对数据进行求和、df.mean()求平均值、df.apply(lambda x:x**2)实现数值平方计算。
Index([u'a', u'b', u'c', u'd'], dtype='object')
Index([u'num'], dtype='object')
num 30
Name: c, dtype: int64
num
b 20
c 30
num 100
dtype: int64
num
a 100
b 400
c 900
d 1600DataFrame对象总体上比较方便、高效,相比ndarray对象更专业化。下面代码是进维度扩增,增加了一个float类型。
df['floats']=(1.5, 2.5, 3.5, 4.5)
print df输出结果如下所示:
num floats
a 10 1.5
b 20 2.5
c 30 3.5
d 40 4.5接下来再增加一个维度,通过索引进行对应。代码如下:
print df['floats']
df['names'] = pd.DataFrame(["Ya","Ga","Ha","Da"],
index=['d','a','b','c'])
print df输出结果如下:
a 1.5
b 2.5
c 3.5
d 4.5
Name: floats, dtype: float64
num floats names
a 10 1.5 Ga
b 20 2.5 Ha
c 30 3.5 Da
d 40 4.5 Ya
2.DatetimeIndex类
接下来我们讲解DatetimeIndex类,通过它定义时间。首先调用numpy.random函数 生成一个9*4的标准正态分布伪随机数,然后定义列标签,代码如下:
# -*- coding: cp936 -*-
import pandas as pd
import numpy as np
a = np.random.standard_normal((9,4))
print a.round(6) #6位小数
#print a
df = pd.DataFrame(a)
df.columns = ["No1", "No2", "No3", "No4"]
print df输出结果如下,如果需要进行访问则调用df['No2'][3]实现。
No1 No2 No3 No4
0 -0.320854 -0.625805 -0.421955 0.389512
1 0.370532 -1.221835 0.010364 1.393511
2 -0.229514 -0.477147 0.128166 -0.619752
3 -0.595702 1.799746 0.330161 1.669275
4 -0.692837 -0.208061 0.576877 1.007649
5 -1.021873 -0.358089 -0.967342 0.894291
6 0.490543 0.261311 -0.366073 0.435141
7 -0.566304 1.673199 -1.733883 -0.292425
8 -0.968336 0.648280 -0.489114 -2.275192dates = pd.date_range('2015-1-1',periods=9,freq='M')
print dates
df.index = dates
print dfB-交易日 D-日 W-每周 M-每月底 MS-月初 BM-每月最后一个交易日 A-每年底 H-每小时
DatetimeIndex(['2015-01-31', '2015-02-28', '2015-03-31', '2015-04-30',
'2015-05-31', '2015-06-30', '2015-07-31', '2015-08-31',
'2015-09-30'],
dtype='datetime64[ns]', freq='M')
No1 No2 No3 No4
2015-01-31 -0.320854 -0.625805 -0.421955 0.389512
2015-02-28 0.370532 -1.221835 0.010364 1.393511
2015-03-31 -0.229514 -0.477147 0.128166 -0.619752
2015-04-30 -0.595702 1.799746 0.330161 1.669275
2015-05-31 -0.692837 -0.208061 0.576877 1.007649
2015-06-30 -1.021873 -0.358089 -0.967342 0.894291
2015-07-31 0.490543 0.261311 -0.366073 0.435141
2015-08-31 -0.566304 1.673199 -1.733883 -0.292425
2015-09-30 -0.968336 0.648280 -0.489114 -2.275192
3.绘图操作
接着我们进行绘图操作,Pandas提供了Matplotlib的一个封装器,专门为Dataframe对象设计。代码如下:
# -*- coding: cp936 -*-
import pandas as pd
import numpy as np
a = np.random.standard_normal((9,4))
df = pd.DataFrame(a)
df.columns = ["No1", "No2", "No3", "No4"]
dates = pd.date_range('2015-1-1',periods=9,freq='M')
df.index = dates
print df.cumsum()
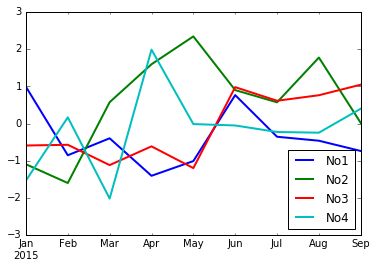
df.plot(lw=2.0)主要调用plot方法,参数包括x、y、title、grid(表格线)、ax、legend、kind(图形类型,kde/line/bar/barh)、logx、yticks(刻度)、xlim(界限)、rot(旋转度)等,绘制图形如下所示:
4.Series类
从DataFrame对象中选择一列时,则得到一个Series对象,代码如下:
# -*- coding: cp936 -*-
import pandas as pd
import numpy as np
a = np.random.standard_normal((9,4))
df = pd.DataFrame(a)
df.columns = ["No1", "No2", "No3", "No4"]
dates = pd.date_range('2015-1-1',periods=9,freq='M')
df.index = dates
print df['No1']
import matplotlib.pyplot as plt
df['No1'].cumsum().plot(style="r",lw=2.)
plt.xlabel('date')
plt.ylabel('value')输出结果如下:
2015-01-31 -0.349526
2015-02-28 -0.511097
2015-03-31 0.987965
2015-04-30 -1.045693
2015-05-31 0.237728
2015-06-30 -0.857229
2015-07-31 0.916528
2015-08-31 1.240449
2015-09-30 -0.687802
Freq: M, Name: No1, dtype: float64仅仅获取了"No1"数据并绘制如下图所示图形:
5.Groupby操作
Pandas具有灵活分组功能,工作方式类似于SQL中分组和Excel透视表,为进行分组,我们添加一组索引对应季度表,代码如下:
# -*- coding: cp936 -*-
import pandas as pd
import numpy as np
a = np.random.standard_normal((9,4))
df = pd.DataFrame(a)
df.columns = ["No1", "No2", "No3", "No4"]
dates = pd.date_range('2015-1-1',periods=9,freq='M')
df.index = dates
df['Quarter'] = ['Q1','Q1','Q1','Q2','Q2','Q2','Q3','Q3','Q3']
print df
groups = df.groupby('Quarter')
print groups.sum()
print groups.mean()
print groups.max()
print groups.size()输出结果如下所示:
No1 No2 No3 No4 Quarter
2015-01-31 0.674688 -0.201858 -0.399297 -0.706358 Q1
2015-02-28 -0.480280 -1.091486 0.667307 -0.039749 Q1
2015-03-31 -0.427795 -0.362502 -0.885939 -1.580051 Q1
2015-04-30 -0.493025 -0.297891 0.748269 -0.128684 Q2
2015-05-31 -1.217889 0.474075 0.146949 0.840250 Q2
2015-06-30 -0.092169 0.541781 0.231801 0.647952 Q2
2015-07-31 0.364487 1.682923 1.561643 0.391411 Q3
2015-08-31 0.353252 -1.086157 0.849758 -0.435598 Q3
2015-09-30 0.805192 -0.434796 0.842751 -0.657201 Q3
No1 No2 No3 No4
Quarter
Q1 -0.233388 -1.655847 -0.617930 -2.326157
Q2 -1.803084 0.717965 1.127018 1.359518
Q3 1.522931 0.161970 3.254152 -0.701388
No1 No2 No3 No4
Quarter
Q1 -0.077796 -0.551949 -0.205977 -0.775386
Q2 -0.601028 0.239322 0.375673 0.453173
Q3 0.507644 0.053990 1.084717 -0.233796
No1 No2 No3 No4
Quarter
Q1 0.674688 -0.201858 0.667307 -0.039749
Q2 -0.092169 0.541781 0.748269 0.840250
Q3 0.805192 1.682923 1.561643 0.391411
Quarter
Q1 3
Q2 3
Q3 3
dtype: int64三. 时间序列算法-ARIMA
作者本来想通过下面代码导入雅虎财经数据,但是没有成功,最终选择自定义数据进行ARIMA算法实验。
时间序列是通过曲线拟合和参数估计来建立 数学模型的理论方法,基本步骤如下:
(1).获取被观测系统时间序列数据;
(2).对数据绘图观测是否为平稳时间序列、非平稳d阶差分;
(3).得平稳时间序列,求其自相关系数ACF和偏自相关系数PACF,通过自相关和偏相关图分析,得到最佳阶层p和结束q;
(4).由d、q、p得到ARIMA模型,然后进行检验。
参考:
Python_Statsmodels包_时间序列分析_ARIMA模型
Python时间序列分析 - 博客园
1.获取数据导入库
# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
dta=[10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085,14722,
11999,9390,13481,14795,15845,15271,14686,11054,10395]
dta = np.array(dta,dtype=np.float) #这里要转下数据类型,不然运行会报错
df = pd.Series(dta)
print df
dates = pd.date_range('2001', periods=90, freq='A')
df.index = dates
print df
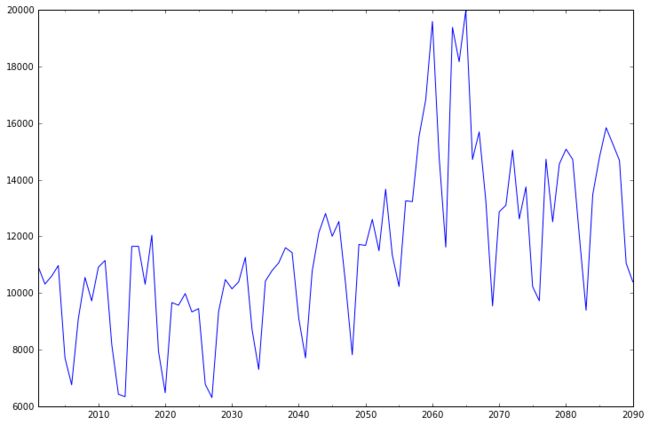
df.plot(figsize=(12,8))2001-12-31 10930.0
2002-12-31 10318.0
2003-12-31 10595.0
2004-12-31 10972.0
2005-12-31 7706.0
....
2086-12-31 15845.0
2087-12-31 15271.0
2088-12-31 14686.0
2089-12-31 11054.0
2090-12-31 10395.0
Freq: A-DEC, Length: 90, dtype: float64绘制图形如下:
2.时间序列差分d
ARIMA模型要求是平稳型,如果是非平稳型的时间序列需要先做时间序列的差分,得到一个平稳的时间序列。如果时间序列做d次差分才能得到一个平稳序列,则可使用ARIMA(p,d,q)模型,其中d表示差分次数。代码如下:
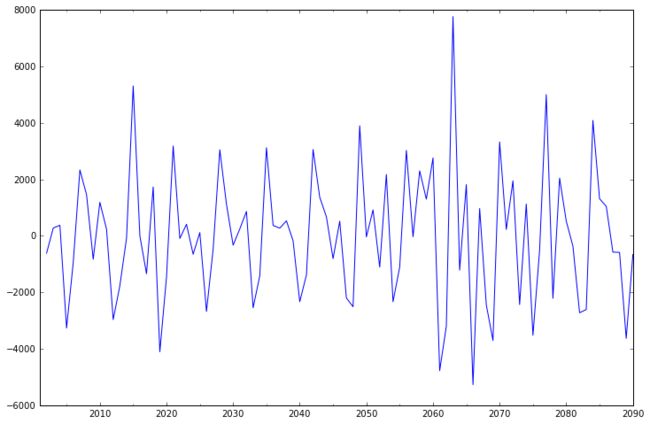
主要调用df.diff(1)实现一阶差分的效果,此数据一阶和二阶差分的结果类似,均值和方差基本问题,这里的差分d值就取1。
# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
dta=[10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085,14722,
11999,9390,13481,14795,15845,15271,14686,11054,10395]
dta = np.array(dta,dtype=np.float) #这里要转下数据类型,不然运行会报错
df = pd.Series(dta)
print df
dates = pd.date_range('2001', periods=90, freq='A')
df.index = dates
print df
df.plot(figsize=(12,8))
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(12,8))
ax1= fig.add_subplot(111)
diff1 = df.diff(1)
diff1.plot(ax=ax1)
注意:差分推导过程作者还在学习中,包括q和p值的计算,如果学会了后面会补充,这里主要是代码的讲解。
3.合适的q和p值
得到一个平稳的时间序列后,需要选择合适的ARIMA模型,即ARIMA模型中的p和q值。
注意:这里需要调用"pip install statsmodels"安装统计数学分析的包,有时您的版本过低会导致错误(尤其是Anaconda 2.7版本),则需要调用"pip install --upgrade statsmodels"升级包至0.8版本。
代码如下:
# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
dta=[10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085,14722,
11999,9390,13481,14795,15845,15271,14686,11054,10395]
dta = np.array(dta,dtype=np.float) #这里要转下数据类型,不然运行会报错
df = pd.Series(dta)
print df
dates = pd.date_range('2001', periods=90, freq='A')
df.index = dates
print df
df.plot(figsize=(12,8))
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(12,8))
ax1= fig.add_subplot(111)
diff1 = df.diff(1)
diff1.plot(ax=ax1)
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
f = plt.figure(facecolor='white')
ax1 = f.add_subplot(211)
plot_acf(df, lags=40, ax=ax1)
ax2 = f.add_subplot(212)
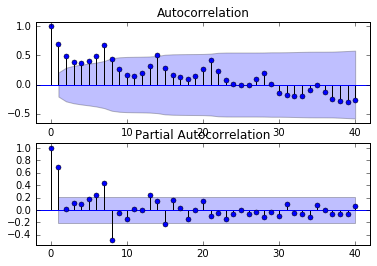
plot_pacf(df, lags=40, ax=ax2)
plt.show()输出结果如下所示,主要 调用plot_acf和plot_pacf函数。
注意:这里根据上述自相关图选择参数,最终选择ARIMA(7,1)模型或ARIMA(8,0)模型,作者也还在研究学习中,后面会补充知识,还请读者原谅。最重要的是第四部分的预测,我认为它是时间序列预测的重点知识。
四. 时间序列预测分析
最后给出选择ARIMA(8,0)模型对未来10年数据进行的代码。代码如下:
# -*- coding: utf-8 -*-
import pandas as pd
import numpy as np
dta=[10930,10318,10595,10972,7706,6756,9092,10551,9722,10913,11151,8186,6422,
6337,11649,11652,10310,12043,7937,6476,9662,9570,9981,9331,9449,6773,6304,9355,
10477,10148,10395,11261,8713,7299,10424,10795,11069,11602,11427,9095,7707,10767,
12136,12812,12006,12528,10329,7818,11719,11683,12603,11495,13670,11337,10232,
13261,13230,15535,16837,19598,14823,11622,19391,18177,19994,14723,15694,13248,
9543,12872,13101,15053,12619,13749,10228,9725,14729,12518,14564,15085,14722,
11999,9390,13481,14795,15845,15271,14686,11054,10395]
dta = np.array(dta,dtype=np.float)
df = pd.Series(dta)
print df
dates = pd.date_range('2001', periods=90, freq='A')
df.index = dates
print df
df.plot(figsize=(12,8))
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(12,8))
ax1= fig.add_subplot(111)
diff1 = df.diff(1)
diff1.plot(ax=ax1)
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
f = plt.figure(facecolor='white')
ax1 = f.add_subplot(211)
plot_acf(df, lags=40, ax=ax1)
ax2 = f.add_subplot(212)
plot_pacf(df, lags=40, ax=ax2)
plt.show()
#预测结果
import statsmodels.api as sm
arma_mod80 = sm.tsa.ARMA(df,(8,0)).fit()
print(arma_mod80.aic, arma_mod80.bic, arma_mod80.hqic)
pre = arma_mod80.predict('2090', '2100', dynamic=True)
print(pre)
fig, ax = plt.subplots(figsize=(12, 8))
ax = df.ix['2000':].plot(ax=ax)
fig = arma_mod80.plot_predict('2090', '2100', dynamic=True, ax=ax, plot_insample=False)
plt.show()(1597.9359982097687, 1622.9340949130715, 1608.0167002177614)
2090-12-31 9542.908069
2091-12-31 12908.529213
2092-12-31 13982.046108
2093-12-31 14501.674565
2094-12-31 13894.459886
2095-12-31 13249.595991
2096-12-31 10960.986520
2097-12-31 10073.503381
2098-12-31 12684.834790
2099-12-31 13477.793055
2100-12-31 13616.117709
Freq: A-DEC, dtype: float64本篇文章为基础性文章,希望对你有所帮助,提供些思路,如果文章中存在错误或不足之处,还请海涵。同时,推荐大家阅读我以前的文章了解基础知识,自己要学习的东西好多啊。
(By:Eastmount 2018-05-09 晚上11点 http://blog.csdn.net/eastmount/ )