直流电磁铁的设计计算

1 设计目标参数

设计的电磁铁需要达到以下性能参数：

推力	最大行程	工作电压	工作电流
195N	2.0mm	28V	3A

2 设计流程

2.1 设计推力的确定

要求在工作时电磁铁推力不小于195N。一般电磁铁在设计时安全系数取1.2。

因此设计推力 Fn=195∗1.2=234N F n = 195 ∗ 1.2 = 234 N ，也就是 F=Fn/9.8=23.88kg F = F n / 9.8 = 23.88 k g 。

取F=24 kg。

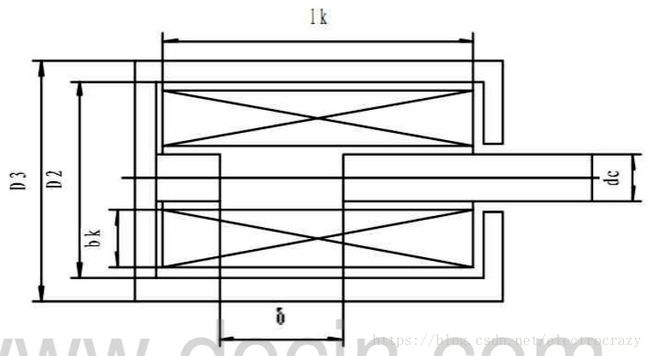
2.2衔铁直径的确定

电磁铁衔铁的工作行程比较小，因此电磁吸力计算时，只需考虑表面力的作用。

已知工作行程 δ=2mm δ = 2 m m 时的吸合力 F=24kg F = 24 k g ，则电磁铁的结构因数：

K=F−−√δ=24−−√0.2=24.5 K = F δ = 24 0.2 = 24.5

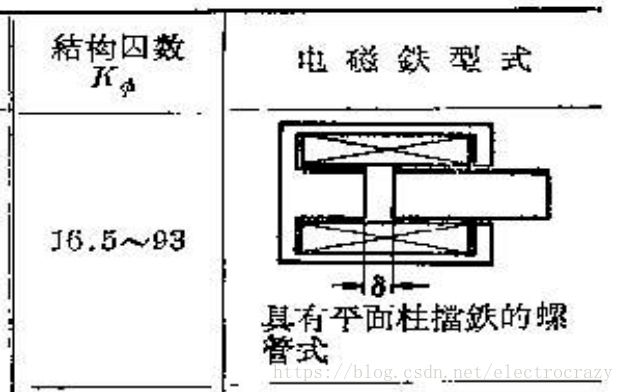
按照资料《电磁铁结构因数与型式关系表》，电磁铁的结构形式应为平面柱挡板中心管式。

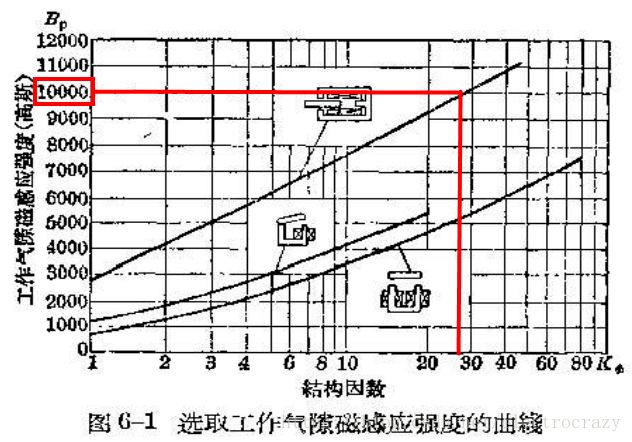
根据同一资料《电磁铁结构因数与型式关系表》里的“图6-1选取工作气隙磁感应强度的曲线”，结构因数 K=24.5 K = 24.5 对应的磁感应强度约等于10000Gs（高斯）。即 Bp=10000Gs B p = 10000 G s 。

当然了此文档是好多年前的了，随着材料技术的进步，现在材料的磁感应强度应该优于 Bp=10000Gs B p = 10000 G s 。

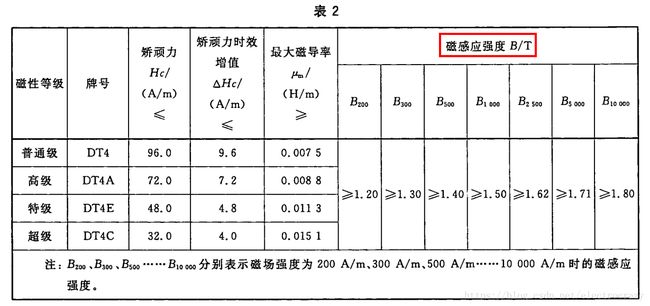
一般电磁铁的铁芯采用DT4系列的电工纯铁材料制作，国标《GB/T 6983-2008：电磁纯铁》中第7.2.3节的表2中有DT4系列材料的特性。

从表中可以看出DT4系列材料的磁感应强度一般在（1.2~1.8）T范围呢。 1T=10000Gs 1 T = 10000 G s 。

崔学琴2004年发表于《中国航空学会控制与应用学术年会》上的文章《YDF-42电磁铁的设计计算》中选择的磁感应强度 Bp=14000Gs B p = 14000 G s 。

综合考虑三方面资料的来源，选取 Bp=14000Gs B p = 14000 G s 。

由吸力公式

F=(Bp5000)2×π4×d2c F = ( B p 5000 ) 2 × π 4 × d c 2

式中： Bp B p ——磁感应强度（ Gs G s ） dc d c ——活动铁芯直径（ mm m m ）

可求得衔铁直径

dc=(5800×F−−√)Bp=(5800×24−−√)14000=2.03cm=20.3mm d c = ( 5800 × F ) B p = ( 5800 × 24 ) 14000 = 2.03 c m = 20.3 m m

取 dc=20mm d c = 20 m m

注：经计算系数应为5642，此处取了5800。 dc d c 的计算值变大，相当于增加了安全系数。

2.3外壳内径的确定

在螺管式电磁铁产品中，外壳内径 D2 D 2 与铁芯直径 dc d c 之比值n约为2~3，取n=2.7

D2=n×dc=2.7×20=54mm D 2 = n × d c = 2.7 × 20 = 54 m m

式中： D2 D 2 ——外壳内径，单位： mm m m 。

2.4线圈厚度的确定

bk=(D2−dc)2−Δ b k = ( D 2 − d c ) 2 − ∆

式中: bk b k ——线圈厚度，单位: mm m m Δ ∆ ——线圈骨架及绝缘厚度，单位: mm m m

取 Δ=1.7mm ∆ = 1.7 m m

bk=(54−20)2−1.7=15.3mm b k = ( 54 − 20 ) 2 − 1.7 = 15.3 m m

取 bk=16mm b k = 16 m m 。

2.5线圈长度的确定

线圈的高度 Ik I k 与厚度 bk b k 比值为 β β ，则线圈高度

Ik=β×bk I k = β × b k

式中： Ik I k ——线圈长度，单位: mm m m

β β 值根据参考资料选取经验数据为 β=3.4 β = 3.4 ，则线圈的高度 Ik=3.4×16=54.4mm I k = 3.4 × 16 = 54.4 m m 。

2.6导线直径的确定

导线直径d的计算公式：

d=(4×ρ×Dcp×IW)U−−−−−−−−−−−−−−−−√ d = ( 4 × ρ × D c p × I W ) U

式中： Dcp D c p ——平均直径，单位: m m

Dcp=dc+bk=0.02+0.016=0.036m D c p = d c + b k = 0.02 + 0.016 = 0.036 m

IW I W ——线圈磁势（安匝）

IW=(IW)z+(IW)cm+(IW)k I W = ( I W ) z + ( I W ) c m + ( I W ) k

式中： (IW)z ( I W ) z ——消耗在气隙中的磁势

(IW)z=(Bp×δ)μ0×10−8 ( I W ) z = ( B p × δ ) μ 0 × 10 − 8

(IW)cm ( I W ) c m 和 (IW)k ( I W ) k ——消耗在铁芯中和非工作气隙中磁势的安匝数，约为总磁势的15~30%，即

(IW)cm+(IW)k=α×IW ( I W ) c m + ( I W ) k = α × I W

式中： α=0.15−0.3 α = 0.15 − 0.3

由此可得线圈的磁势为

IW=(Bp×δ)μ0×(1−α)×10−8（安匝） I W = ( B p × δ ) μ 0 × ( 1 − α ) × 10 − 8 （ 安 匝 ）

式中： Bp B p 单位： Gs G s ， δ δ 单位： cm c m ，空气导磁系数： μ0=1.25×10−8H/cm μ 0 = 1.25 × 10 − 8 H / c m

电磁铁在实际应用时，电压可能降低至85% UH U H ，为了保证在电压降低后，电磁铁仍然能够可靠的工作，上式计算所得安匝数应该是指电压降低至85% UH U H 时的磁势，用 (IW)1 ( I W ) 1 表示

(IW)1=14000×0.21.25×10−8×（1−0.3）×10−8=3200安匝 ( I W ) 1 = 14000 × 0.2 1.25 × 10 − 8 × （ 1 − 0.3 ） × 10 − 8 = 3200 安 匝

电源电压为额定值时的磁势为

IW=(IW)10.85=3764.7安匝 I W = ( I W ) 1 0.85 = 3764.7 安 匝

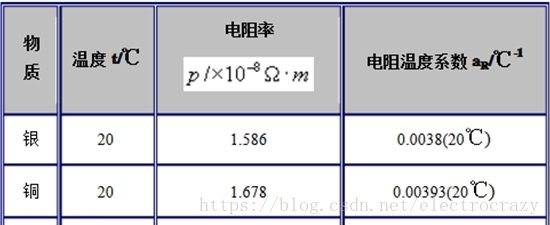
电磁铁设计时一般取工作温度为150℃，由下表可知，20℃时铜的电阻率 ρ20=1.678×10−8Ω∙m ρ 20 = 1.678 × 10 − 8 Ω • m ，温度系数 αR=0.00393℃−1 α R = 0.00393 ℃ − 1 。则100℃时铜的电阻率

ρ100=ρ20×(1+αR×(100−20)) ρ 100 = ρ 20 × ( 1 + α R × ( 100 − 20 ) )

ρ100=2.2055×10−8Ω∙m=0.022056Ω×(mm)2/m ρ 100 = 2.2055 × 10 − 8 Ω • m = 0.022056 Ω × ( m m ) 2 / m

d=4×ρ×Dcp×IWU−−−−−−−−−−−−−−−√=4×0.022056×0.036×3764.728−−−−−−−−−−−−−−−−−−−−−−−−√=0.6535mm d = 4 × ρ × D c p × I W U = 4 × 0.022056 × 0.036 × 3764.7 28 = 0.6535 m m

查线规表，依据国标《GB/T6109.1-2008漆包圆绕组线第1部分：一般规定》中关于漆包线直径的规定，选择最接近的线径 d=0.67mm d = 0.67 m m 。带绝缘后的直径 d=0.749mm d = 0.749 m m （2级）。

2.7线圈匝数W的确定

W=1.28×IWj×d2 W = 1.28 × I W j × d 2

式中： j j ——容许电流密度（ A/mm2 A / m m 2 ），

j=Iq=4Iπ×d2=4×3π×0.672=8.5091A/mm2 j = I q = 4 I π × d 2 = 4 × 3 π × 0.67 2 = 8.5091 A / m m 2

W=1.28×(IW)jd2=1.28×3764.78.5091×0.67×0.67=1261.5576匝≈1262匝 W = 1.28 × ( I W ) j d 2 = 1.28 × 3764.7 8.5091 × 0.67 × 0.67 = 1261.5576 匝 ≈ 1262 匝

注：电流I取3A，工作参数中已给定。

2.8电阻的确定

线圈平均匝长

lcp=π×(DH+D1)2 l c p = π × ( D H + D 1 ) 2

DH=D1+2bk D H = D 1 + 2 b k

D1=dc+2Δ D 1 = d c + 2 ∆

式中： DH D H ——线圈外直径

D1 D 1 ——线圈内直径

D1=dc+2Δ=20+2×1.7=23.4mm D 1 = d c + 2 ∆ = 20 + 2 × 1.7 = 23.4 m m

DH=D1+2bk=23.4+2×16=55.4mm D H = D 1 + 2 b k = 23.4 + 2 × 16 = 55.4 m m

lcp=π×(DH+D1)2=π×(55.4+23.4)2=123.78mm=0.12378m l c p = π × ( D H + D 1 ) 2 = π × ( 55.4 + 23.4 ) 2 = 123.78 m m = 0.12378 m

线圈电阻

R=ρ40×lcp×Wπ4×d2=0.01991×0.12378×1262π4×0.672=8.8215Ω R = ρ 40 × l c p × W π 4 × d 2 = 0.01991 × 0.12378 × 1262 π 4 × 0.67 2 = 8.8215 Ω

3 特性验算

虽然已经完成初步设计，但是在初步设计中作了不少简化，有些参数的选择和估计是极其近似的。因此为了电磁铁工作可靠，还需要根据初步设计的结构尺寸和数据做进一步详细的验算。

3.1吸力计算

F=(∅5000)2×1S(1+αδ) F = ( ∅ 5000 ) 2 × 1 S ( 1 + α δ )

忽略铁磁阻和漏磁通，这样气隙中的磁通

∅Z=IW×GZ×108 ∅ Z = I W × G Z × 10 8

式中：磁导 GZ=μ0×πd2c4δ G Z = μ 0 × π d c 2 4 δ ，空气导磁系数 μ0=1.25×10−8H/cm μ 0 = 1.25 × 10 − 8 H / c m

GZ=μ0×πd2c4δ=1.25×10−8×π×224×0.2=19.635×10−8H G Z = μ 0 × π d c 2 4 δ = 1.25 × 10 − 8 × π × 2 2 4 × 0.2 = 19.635 × 10 − 8 H

∅Z=IW×GZ×108=3764.7×19.635=73919.71Mx ∅ Z = I W × G Z × 10 8 = 3764.7 × 19.635 = 73919.71 M x

式中： α α ——修正系数，一般取3~4，这里取 α=4 α = 4 S S ——铁芯截面积

S=πd2c4=π×224=3.14159cm2 S = π d c 2 4 = π × 2 2 4 = 3.14159 c m 2

F=(∅5000)2×1S(1+αδ)=(73919.715000)2×13.1416(1+4×0.2)=38.65公斤 F = ( ∅ 5000 ) 2 × 1 S ( 1 + α δ ) = ( 73919.71 5000 ) 2 × 1 3.1416 ( 1 + 4 × 0.2 ) = 38.65 公 斤

计算出来的推力大于设计推力，因此以上设计参数使可取的。

【参考】
（1） 论文：《YDF-42电磁铁的设计计算》 作者：崔学琴
（2） 资料：《电磁铁结构因数与型式关系表》 网址：https://wenku.baidu.com/view/ec1221909b89680202d82507.html
（3） 国标：《GB/T 6983-2008：电磁纯铁》
（4） 国标：《GB/T 6109.1-2008漆包圆绕组线第1部分：一般规定》
（5） 论文：《各种结构形式电磁铁通用的磁路计算公式和方法》作者：左全璋
（6） 论文：《电磁铁吸力计算及仿真分析研究》 作者：梅亮 等