退而求其次(3)——宿管员的烦恼

　　书接上文，在《退而求其次(1)——随机法》中宿管员使用了随机法分配宿舍，现在尝试使用遗传算法。

顺序编码和初始种群

　　遗传算法的首要问题是基因编码。对于分宿舍问题，每种分配方案是一个个体，其基因序列的每一个编码代表一个同学，要求处于同一基因序列中的所有基因代码均不能重复，也就是每个同学都是独一无二的。在这种规则下，使用二进制编码就显得笨拙了。一种简单的编码方案是直接使用同学的序号作为基因编码，这种编码称为顺序码。

　　顺序码又称自然数编码，使用从1到n 的自然数进行编码，且不允许重复。例如[1,2,3,4,5,6,7,8,9,10,11,12]是一个合法的个体，表示按编码从左到右的顺序四人一个宿舍，而[1,1,3,3,6,6,8,8,9,10,11,12]则不是。

　　随机选择1000个个体作为初始种群，约占解空间的20%：

1 POPULATION_SIZE = 1000 # 种群数量
2
3 def init_population():
4     ''' 构造初始种群 '''
5     population = []
6     code_len = len(base_data.STUDENTS_NAME)  # 编码长度
7     for i in range(POPULATION_SIZE):
8         population.append(base_data.upset())
9     return population

适应度评估和种群选择

　　可以利用成本函数cost_fun来进行适应度评估。由于cost_fun识别的是解而不是基因编码，因此在使用cost_fun之前还需要通过solution_adapter将基因编码适配成解，将基因编码[1,2,3,4,5,6,7,8,9,10,11,12]翻译成cost_fun能够有效计算的[[1,2,3,4],[5,6,7,8],[9,10,11,12]]。

 1 def solution_adapter(code):
 2     ''' 将基因编码翻适配成cost_fun能够识别的解 '''
 3     solution = []
 4     for i in range(0, len(base_data.STUDENTS_NAME), base_data.NUM_PER_DROM):
 5         solution.append(code[i:i + base_data.NUM_PER_DROM])
 6     return solution
 7
 8 def fitness_fun(code):
 9     '''
10     适应度评估
11     :param code:   二进制基因编码
12     :return: 适应度评估值, 二元组, (宿舍总成本, 每个宿舍的成本)
13     '''
14     return base_data.cost_fun(solution_adapter(code))

　　我们依然使用锦标赛法选择种群。由于成本越低表示适应度越越高，因此在锦标赛中适应度值低的是胜出者。

1 def selection(population):
2     '''选择策略, 锦标赛法'''
3     pop_next = []  # 下一代种群
4     for i in range(POPULATION_SIZE):
5         tour_list = random.choices(population, k=2) # 二元锦标赛
6         winner = min(tour_list, key=lambda x: fitness_fun(x)) # 成本低的胜出
7         pop_next.append(winner)
8     return pop_next

部分匹配交叉和循环交叉

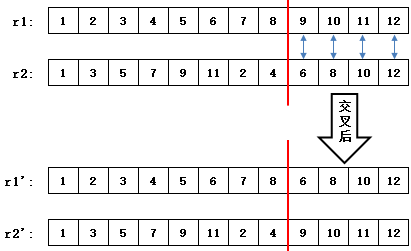
　　对于宿舍编码来说，单点交叉和两点交叉都无法产生合法的个体，下图展示了一个不合法的单点交叉。

　　在交叉后的个体 r1' 中，基因代码6和8出现了两次，表示6号同学和8号同学同时住在两个宿舍，这显然不是一个合法的解。反过来，如果交叉后得到了合法的个体，那么新个体又会和它们的父代没有任何区别，即没有产生任何新个体：

　　r1和 r1' 没有任何区别，最后一个宿舍的四个同学仅仅是交换了一下床位。看来必须另辟他径，寻找其它的交叉策略。

部分匹配交叉

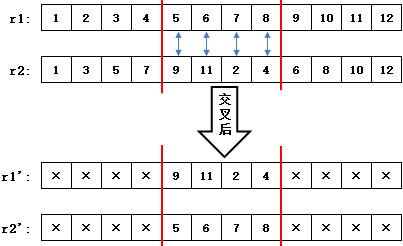
　　部分匹配交叉（Partially Matched Crossover，PMC）在1985年被提出，是由两点交叉改进而来的。部分匹配交叉的第一步和两点交叉一样，首先在个体基因序列中随机设置两个交叉点，然后随机选择两个个体做为父代个体，相互交换它们交叉点之间的那部分基因块

　　在交叉时需要记住交叉前的基因块r1→[5,6,7,8]，r2→[9,11,2,4] 。

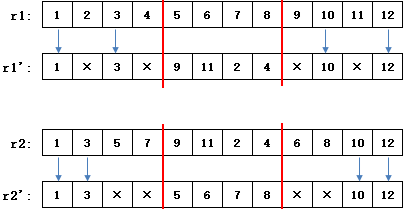
　　接下来对交叉后生成的新个体 r1' 和 r2' 中的×部分，分别继承r1和 r2 中对应位置的编码，如果待继承的编码在交换后的基因块中，则不做继承：

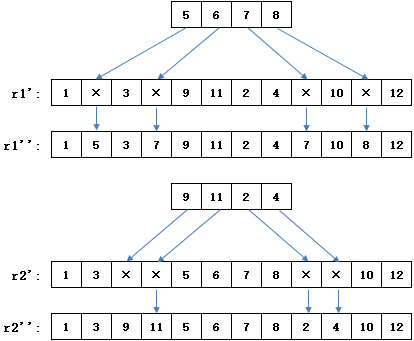
　　最后，把交叉前记住的基因块按顺序依次填入×部分，得到最终的r1'和 r2' ：

　　如果交叉前的编码已经在 r1' 中，则略过该编码。下图在替换x时需要略过2和6：

　　r1 是初始个体，它的基因块[2,4,6,9]与另一个个体的对应基因块[2,6,7,8]交叉，得到[×,×,×,×.2,6,7,8,×,×,×,×]。继承 r1 后得到 r1' = [1,3,5,×,2,6,7,8,×,10,11,12]。在[2,4,6,9]中，编码2和6已经在 r1' 中，因此只有4和9可以替换对应的×。

　　部分匹配交叉的编码如下。

 1 def crossover_pmc(population):
 2     ''' 部分匹配交叉（PMC）'''
 3
 4     def create_mapping(cross_code_1, cross_code_2):
 5         '''
 6         建立两个交叉片段间的映射关系
 7         :param cross_code_1:
 8         :param cross_code_2:
 9         :return:  映射关系set
10         '''
11         mapping = set()
12         for i in range(len(cross_code_1)):
13             c1, c2 = cross_code_1[i], cross_code_2[i]
14             if (c1, c2) not in mapping and  (c2, c1) not in mapping:
15                 mapping.add((c1, c2))
16         return mapping
17
18     def code_extends(child, parent, start, end):
19         '''
20         继承父代的编码
21         :param child: 子代个体
22         :param parent: 父代个体
23         :param start: 基因编码起始位置
24         :param end: 基因编码终止位置
25         '''
26         for i in range(start, end):
27            if parent[i] not in child:
28                child[i] = parent[i]
29
30     def code_rest(child, cross_code):
31         '''
32         通交叉前的基因片段修改子代的编码
33         :param child: 子代个体
34         :param cross_code: 交叉前的的基因片段
35         :return:
36         '''
37         for i, x in enumerate(child):
38             if x != -1:
39                 continue
40             for x_old in cross_code:
41                 if x_old not in child:
42                     child[i] = x_old
43                     break
44
45     pop_new = []  # 新种群
46     code_len = len(population[0])  # 基因编码的长度
47     for i in range(POPULATION_SIZE):
48         # 选择两个随机的交叉点
49         p1, p2 = random.randint(0, code_len - 1), random.randint(0, code_len - 1)
50         if p1 > p2:
51             p1, p2 = p2, p1
52         parent1, parent2 = random.choices(population, k=2)  # 选择两个随机的个体
53         cross_code_1 = parent1[p1:p2] # 交叉前的编码块
54         cross_code_2 = parent2[p1:p2] # 交叉后的编码块
55         # 构造新的个体，-1表示基因编码尚未确定
56         r = [-1] * p1 + cross_code_2 + [-1] * (code_len - p2)
57         code_extends(r, parent1, 0, p1) #  继承父代的编码
58         code_extends(r, parent1, p2, code_len) #  继承父代的编码
59         mapping = create_mapping(cross_code_1, cross_code_2) # 两个交叉块的映射关系
60         code_rest(r, cross_code_1)  # 通过交换前的基因片段确定剩余编码
61         pop_new.append(r)
62     return pop_new

循环交叉

　　循环交叉（Cycle Crossover，CX）是另一种适合顺序编码的交叉策略。不同于其它交叉策略，循环交叉不需事先要选择交叉点。

　　假设有两个父代个体

　　先从 r1 中选择第0个编码，作为子代 r1' 的第一个编码：

　　r2 的第0个编码是2，因此 r1' 中第2个被确定的编码是2：

　　2在 r1 中的序号是1， r2[1]=3, r1' 中第3个确定的编码是3：

　　3在 r1 中的序号是2， r2[2]=5， r1' 中第4个确定的编码是5：

　　5在 r1 中的序号是3， r2[3]=1 ， 和 r1' 中第1个编码相同，至此称为一个循环。剩余未确定的编码从 r2 的对应位置映射即可

　　循环交叉匹配的代码如下：

 1 def crossover_cx(population):
 2     ''' 循环交叉匹配 '''
 3     pop_new = []  # 新种群
 4     code_len = len(population[0])  # 基因编码的长度
 5     for i in range(POPULATION_SIZE):
 6         parent1, parent2 = random.choices(population, k=2)  # 选择两个随机的个体
 7         r_new = [-1] * code_len  # 新个体
 8         r_new[0] = parent1[0]
 9         i = 0
10         while True:  # 循环交叉
11             x = parent2[i]
12             if r_new[0] == x:
13                 break
14             i = parent1.index(x)
15             r_new[i] = x
16         # r_new中剩余未确定的编码直接从parent2中继承
17         for i, x in enumerate(r_new):
18             if x == -1:
19                 r_new[i] = parent2[i]
20         pop_new.append(r_new)
21     return pop_new

变异

　　顺序编码的变异策略很简单，仅仅是将两个随机变异点的编码互相交换：

 1 def mutation(population):
 2     ''' 变异 '''
 3     code_len = len(population[0])  # 基因编码的长度
 4     mp = 0.2  # 变异率
 5     for i, r in enumerate(population):
 6         if random.random() < mp:
 7             # 两个随机变异点
 8             p1, p2 = random.randint(0, code_len - 1), random.randint(0, code_len - 1)
 9             # 交换两个变异点的数据
10             population[p1], population[p2] = population[p2], population[p1]

分配宿舍

　　准备工作已经就绪，可以开始使用遗传算法分配宿舍：

 1 def sum_fitness(population):
 2     ''' 计算种群的总适应度 '''
 3     return sum([fitness_fun(code)[0] for code in population])
 4
 5 def ga():
 6     ''' 遗传算法分配宿舍 '''
 7     population = init_population() # 构建初始化种群
 8     s_fitness = sum_fitness(population) # 种群的总适应度
 9     i = 0
10     while i < 10: # 如果连续10代没有改进，结束算法
11         pop_next = selection(population) # 选择种群
12         pop_new = crossover_cx(pop_next) # 交叉
13         mutation(pop_new) # 变异
14         s_fitness_new = sum_fitness(pop_new) # 新种群的总适应度
15         if s_fitness > s_fitness_new: # 成本越低，适应度越高
16             s_fitness = s_fitness_new
17             i = 0
18         else:
19             i += 1
20         population = pop_new
21     # 按适应度值从大到小排序
22     population = sorted(population, key=lambda x: fitness_fun(x), reverse=True)
23     # 返回最优的个体
24     return population[0]
25
26 if __name__ == '__main__':
27     best = ga()
28     solution = solution_adapter(best)
29     total_cost, dorms_cost = base_data.cost_fun(solution)
30     base_data.print_solution(solution, total_cost, dorms_cost)

　　需要注意的是第15行的适应度比较，由于这里使用的是成本函数，因此种群的成本值越低，适应度越高，越应该被保留。一种可能的运行结果：

　　可以看到，在总成本较低的同时，“不均”的问题也得到了解决。

总体代码

　　base_data.py:

  1 import random
  2
  3 # 学生调查表数据
  4 STUDENTS = [
  5     [32, 1, 2, 2, [11, 33, 42], 5],
  6     [32, 1, 2, 1, [11], 5],
  7     [41, 1, 2, 5, [21, 22], 4],
  8     [43, 2, 3, 3, [11, 21], 3],
  9     [36, 2, 3, 4, [11, 33], 3],
 10     [44, 2, 3, 4, [41, 42], 2],
 11     [42, 1, 2, 1, [11, 12], 1],
 12     [32, 1, 1, 2, [31, 32], 2],
 13     [61, 1, 1, 3, [51], 3],
 14     [61, 1, 1, 2, [13], 3],
 15     [44, 3, 4, 1, [21, 43], 1],
 16     [22, 3, 4, 4, [22, 43], 2]
 17 ]
 18 # 学生姓名
 19 STUDENTS_NAME = ['蕾娜', '琪琳', '蔷薇', '炙心',
 20                  '灵犀', '莫伊', '怜风', '语琴',
 21                  '凉冰', '鹤熙', '瑞萌萌', '何蔚蓝']
 22 DROM_SIZE = 3  # 宿舍数量
 23 NUM_PER_DROM = 4 # 每个宿舍的人数
 24 MAX_COST = 5 # 同一维度间的最大差异
 25
 26 def cost_stu(stu_1, stu_2):
 27     ''' 以stu_1为主，计算stu_1与stu_2的差异 '''
 28     cost = [] # 各维度的成本值（差异度）
 29     cost.append(cost_equal(stu_1[0], stu_2[0])) # 籍贯成本
 30     cost.append(cost_equal(stu_1[1], stu_2[1])) # 专业成本
 31     cost.append(cost_class(stu_1[2], stu_2[2], stu_1[1], stu_2[1])) # 班级成本
 32     cost.append(cost_get_up(stu_1[3], stu_2[3])) # 起床成本
 33     cost.append(cost_interest(stu_1[4], stu_2[4])) # 爱好成本
 34     w_idx_1, w_idx_2 = stu_1[len(stu_1) - 1] - 1, stu_2[len(stu_2) - 1] - 1 # 权重序号
 35     w_cost_1, w_cost_2 = cost[w_idx_1] * 1.5,  cost[w_idx_2] * 1.5  # 加权处理
 36     # 判断二者最在意的是否相同
 37     if w_idx_1 == w_idx_1:
 38         cost[w_idx_1] = w_cost_1 + w_cost_2
 39     else:
 40         cost[w_idx_1], cost[w_idx_2] = w_cost_1, w_cost_2
 41
 42     return sum(cost)
 43
 44 def cost_equal(d_1, d_2):
 45     ''' 同质化比较成本  '''
 46     return 0 if d_1 == d_2 else MAX_COST
 47
 48 def cost_class(d_1, d_2, sub_1, sub_2):
 49     ''' 班级成本 '''
 50     if d_1 == d_1: # 班级相同
 51         return 0
 52     elif sub_1 == sub_1: # 不同班级，同一专业
 53         return 1
 54     else: # 不同班级，不同专业
 55         return MAX_COST
 56
 57 def cost_get_up(d_1, d_2):
 58     ''' 起床成本 '''
 59     return 1.2 * (d_2 - d_1)
 60
 61 def cost_interest(d_1, d_2):
 62     ''' 爱好成本 '''
 63     for t_1 in d_1:
 64         # 如果两个同学都有一个共同的爱好，二者就是零距离
 65         if t_1 in d_2:
 66             return 0
 67
 68         obj_1 = t_1 // 10 # 爱好的“大类”
 69         # 如果两个同学都有一个共同的大类，二者距离是2
 70         for t_2 in d_2:
 71             if obj_1 == t_2 // 10:
 72                 return 2
 73     return MAX_COST
 74
 75 def cost_fun(solution):
 76     '''
 77     计算方案中每个宿舍的成本
 78     :param solution: 宿舍分配方案
 79     :return: 宿舍总成本和每个宿舍的成本
 80     '''
 81     droms_cost = []
 82     for drom in solution:
 83         # 同一宿舍中的四个同学两两比对
 84         d_cost = 0
 85         d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[1]])
 86         d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[2]])
 87         d_cost += cost_stu(STUDENTS[drom[0]], STUDENTS[drom[3]])
 88         d_cost += cost_stu(STUDENTS[drom[1]], STUDENTS[drom[2]])
 89         d_cost += cost_stu(STUDENTS[drom[1]], STUDENTS[drom[3]])
 90         d_cost += cost_stu(STUDENTS[drom[2]], STUDENTS[drom[3]])
 91         droms_cost.append(d_cost)
 92     diff_cost = max(droms_cost) - min(droms_cost) # 宿舍之间的贫富差
 93     total_cost = sum(droms_cost) + diff_cost * DROM_SIZE # 该方案的总成本
 94     return total_cost, droms_cost
 95
 96 def upset():
 97     ''' 打乱学生顺序 '''
 98     n = len(STUDENTS_NAME)
 99     stu_list = list(range(n))
100     # 打乱学生顺序
101     for i in range(n):
102         rand_idx = random.randint(0, n - 1)
103         stu_list[i], stu_list[rand_idx] = stu_list[rand_idx], stu_list[i]
104     return stu_list
105
106 def print_solution(solution, total_cost, dorms_cost):
107     for i, drom in enumerate(solution):
108         print('宿舍%d:\t' % i, end='')
109         for j in drom:
110             print('%-8s' % STUDENTS_NAME[j], end='')
111         print('\tcost=%f' % dorms_cost[i])
112     print('total=%f' % total_cost)

genetic_optimize.py

  1 from __future__ import division
  2 import random
  3 import os
  4 import sys
  5 parent_dir_name = os.path.dirname(os.path.realpath(__file__))
  6 sys.path.append(parent_dir_name )
  7 import base_data
  8
  9 POPULATION_SIZE = 1000 # 种群数量
 10
 11 def init_population():
 12     ''' 构造初始种群 '''
 13     population = []
 14     code_len = len(base_data.STUDENTS_NAME)  # 编码长度
 15     for i in range(POPULATION_SIZE):
 16         population.append(base_data.upset())
 17     return population
 18
 19 def solution_adapter(code):
 20     ''' 将基因编码翻适配成cost_fun能够识别的解 '''
 21     solution = []
 22     for i in range(0, len(base_data.STUDENTS_NAME), base_data.NUM_PER_DROM):
 23         solution.append(code[i:i + base_data.NUM_PER_DROM])
 24     return solution
 25
 26 def fitness_fun(code):
 27     '''
 28     适应度评估
 29     :param code:   二进制基因编码
 30     :return: 适应度评估值, 二元组, (宿舍总成本, 每个宿舍的成本)
 31     '''
 32     return base_data.cost_fun(solution_adapter(code))
 33
 34 def selection(population):
 35     '''选择策略, 锦标赛法'''
 36     pop_next = []  # 下一代种群
 37     for i in range(POPULATION_SIZE):
 38         tour_list = random.choices(population, k=2) # 二元锦标赛
 39         winner = min(tour_list, key=lambda x: fitness_fun(x)) # 成本低的胜出
 40         pop_next.append(winner)
 41     return pop_next
 42
 43 def crossover_pmc(population):
 44     ''' 部分匹配交叉（PMC）'''
 45
 46     def create_mapping(cross_code_1, cross_code_2):
 47         '''
 48         建立两个交叉片段间的映射关系
 49         :param cross_code_1:
 50         :param cross_code_2:
 51         :return:  映射关系set
 52         '''
 53         mapping = set()
 54         for i in range(len(cross_code_1)):
 55             c1, c2 = cross_code_1[i], cross_code_2[i]
 56             if (c1, c2) not in mapping and  (c2, c1) not in mapping:
 57                 mapping.add((c1, c2))
 58         return mapping
 59
 60     def code_extends(child, parent, start, end):
 61         '''
 62         继承父代的编码
 63         :param child: 子代个体
 64         :param parent: 父代个体
 65         :param start: 基因编码起始位置
 66         :param end: 基因编码终止位置
 67         '''
 68         for i in range(start, end):
 69            if parent[i] not in child:
 70                child[i] = parent[i]
 71
 72     def code_rest(child, cross_code):
 73         '''
 74         通交叉前的基因片段修改子代的编码
 75         :param child: 子代个体
 76         :param cross_code: 交叉前的的基因片段
 77         :return:
 78         '''
 79         for i, x in enumerate(child):
 80             if x != -1:
 81                 continue
 82             for x_old in cross_code:
 83                 if x_old not in child:
 84                     child[i] = x_old
 85                     break
 86
 87     pop_new = []  # 新种群
 88     code_len = len(population[0])  # 基因编码的长度
 89     for i in range(POPULATION_SIZE):
 90         # 选择两个随机的交叉点
 91         p1, p2 = random.randint(0, code_len - 1), random.randint(0, code_len - 1)
 92         if p1 > p2:
 93             p1, p2 = p2, p1
 94         parent1, parent2 = random.choices(population, k=2)  # 选择两个随机的个体
 95         cross_code_1 = parent1[p1:p2] # 交叉前的编码块
 96         cross_code_2 = parent2[p1:p2] # 交叉后的编码块
 97         # 构造新的个体，-1表示基因编码尚未确定
 98         r = [-1] * p1 + cross_code_2 + [-1] * (code_len - p2)
 99         code_extends(r, parent1, 0, p1) #  继承父代的编码
100         code_extends(r, parent1, p2, code_len) #  继承父代的编码
101         mapping = create_mapping(cross_code_1, cross_code_2) # 两个交叉块的映射关系
102         code_rest(r, cross_code_1)  # 通过交换前的基因片段确定剩余编码
103         pop_new.append(r)
104     return pop_new
105
106 def crossover_cx(population):
107     ''' 循环交叉匹配 '''
108     pop_new = []  # 新种群
109     code_len = len(population[0])  # 基因编码的长度
110     for i in range(POPULATION_SIZE):
111         parent1, parent2 = random.choices(population, k=2)  # 选择两个随机的个体
112         r_new = [-1] * code_len  # 新个体
113         r_new[0] = parent1[0]
114         i = 0
115         while True:  # 循环交叉
116             x = parent2[i]
117             if r_new[0] == x:
118                 break
119             i = parent1.index(x)
120             r_new[i] = x
121         # r_new中剩余未确定的编码直接从parent2中继承
122         for i, x in enumerate(r_new):
123             if x == -1:
124                 r_new[i] = parent2[i]
125         pop_new.append(r_new)
126     return pop_new
127
128 def mutation(population):
129     ''' 变异 '''
130     code_len = len(population[0])  # 基因编码的长度
131     mp = 0.2  # 变异率
132     for i, r in enumerate(population):
133         if random.random() < mp:
134             # 两个随机变异点
135             p1, p2 = random.randint(0, code_len - 1), random.randint(0, code_len - 1)
136             # 交换两个变异点的数据
137             population[p1], population[p2] = population[p2], population[p1]
138
139 def sum_fitness(population):
140     ''' 计算种群的总适应度 '''
141     return sum([fitness_fun(code)[0] for code in population])
142
143 def ga():
144     ''' 遗传算法分配宿舍 '''
145     population = init_population() # 构建初始化种群
146     s_fitness = sum_fitness(population) # 种群的总适应度
147     i = 0
148     while i < 10: # 如果连续10代没有改进，结束算法
149         pop_next = selection(population) # 选择种群
150         pop_new = crossover_cx(pop_next) # 交叉
151         mutation(pop_new) # 变异
152         s_fitness_new = sum_fitness(pop_new) # 新种群的总适应度
153         if s_fitness > s_fitness_new: # 成本越低，适应度越高
154             s_fitness = s_fitness_new
155             i = 0
156         else:
157             i += 1
158         population = pop_new
159     # 按适应度值从大到小排序
160     population = sorted(population, key=lambda x: fitness_fun(x), reverse=True)
161     # 返回最优的个体
162     return population[0]
163
164 if __name__ == '__main__':
165     best = ga()
166     solution = solution_adapter(best)
167     total_cost, dorms_cost = base_data.cost_fun(solution)
168     base_data.print_solution(solution, total_cost, dorms_cost)

---

　　 作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注公众号“我是8位的”