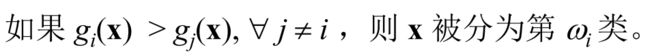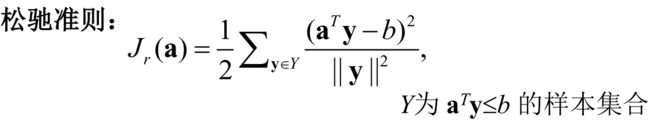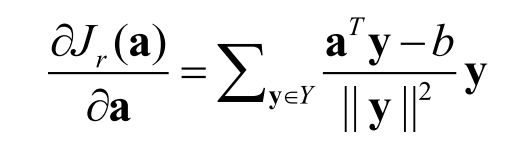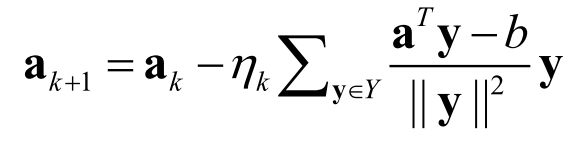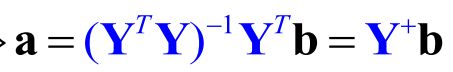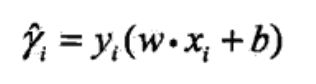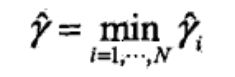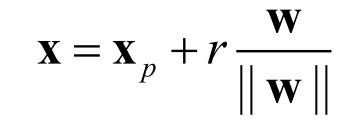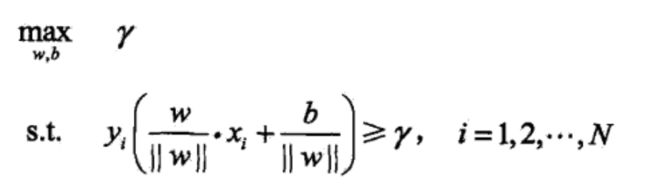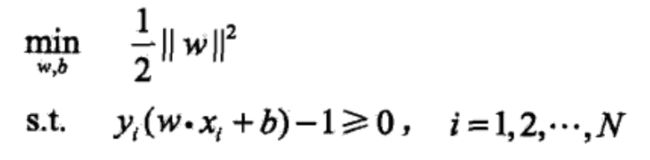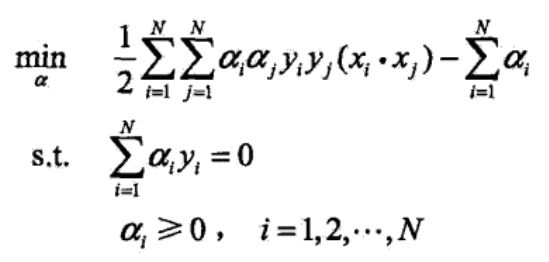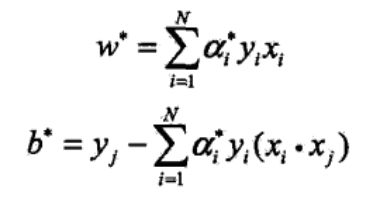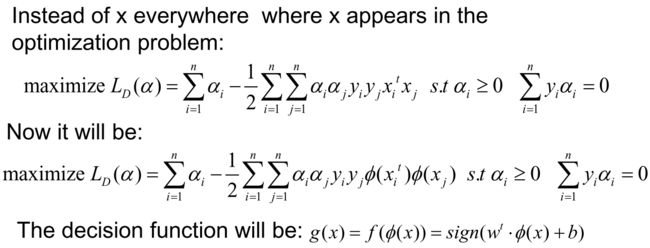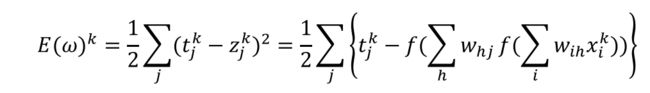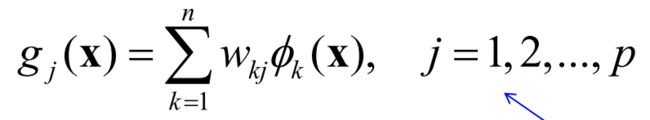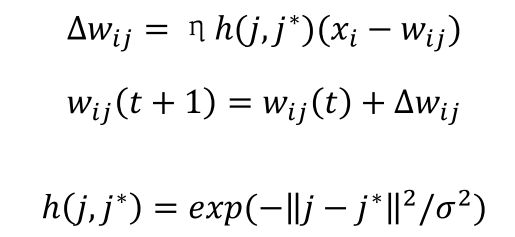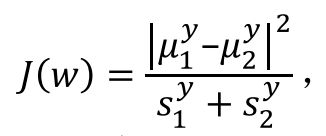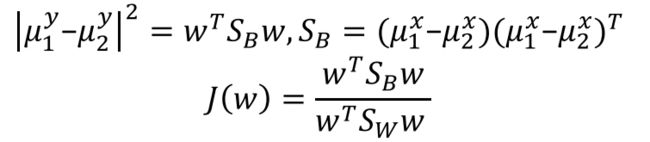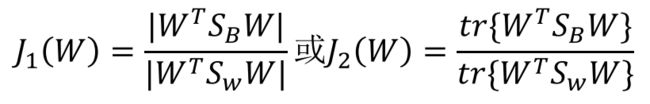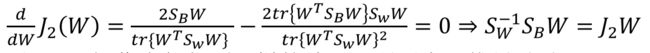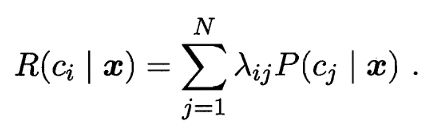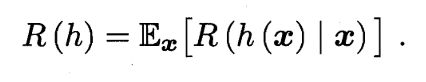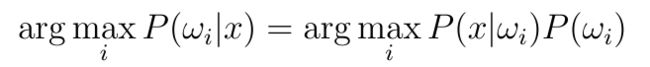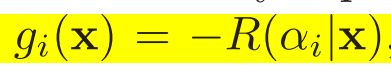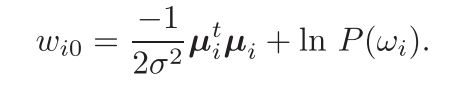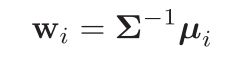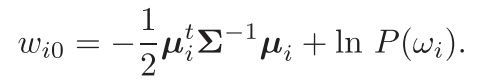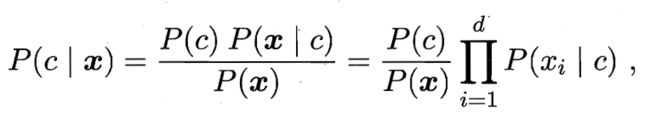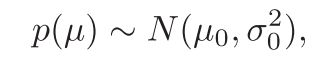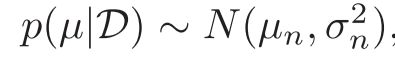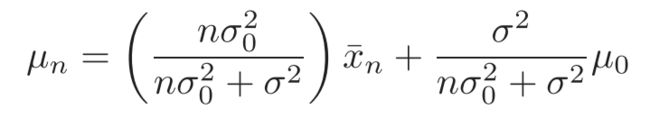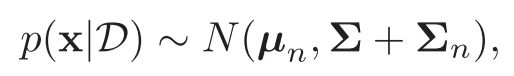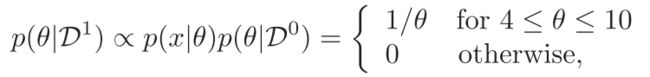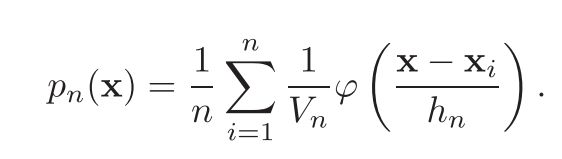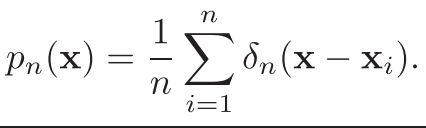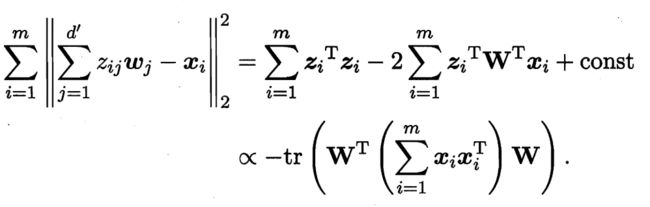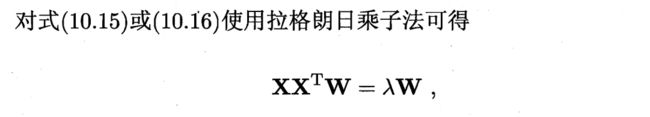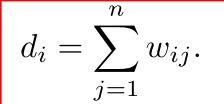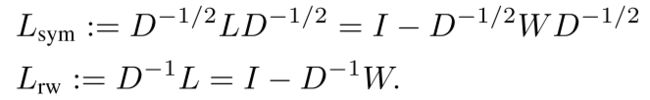模式识别复习整理

考试说明

注重基础知识和概念的理解，因此解题中的计算过程不会很复杂，但是会有推公式的过程。本课程的重点知识包括：贝叶斯决策、概率密度估计、参数法、非参数法、线性分类器设计、神经网络、支撑向量机、聚类分析、特征提取和选择。

参考资料：

• 《机器学习》周志华： p
• 《统计学习方法》李航：*p
• 'Pattern Classification 2nd'：%p
• 'Pattern Classification and Machine Learning' :[pclm]
• ‘A Tutorial on Spectral Clustering’ [tsc]
• neural-networks-and-deep-learning [nndl]

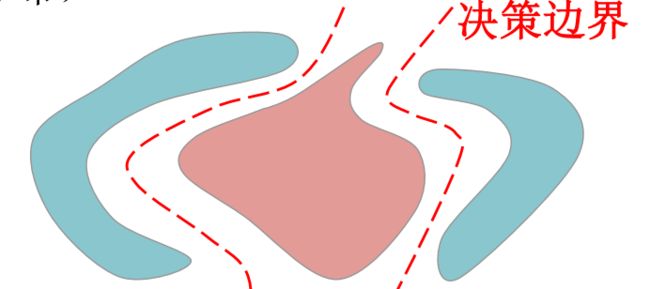
本文结构：哪些分类模型属于参数法/非参数法？哪些属于生成模型/判别模型？

• 生成模型是基于概率密度的，会显式地计算后验概率/类条件概率。将后验概率/类条件概率计算出来后，根据贝叶斯决策，可以得到最小误差判别/最小风险判别。计算后验概率/类条件概率可以分为参数法和非参数法：
  • 参数法：假设总体服从某含参数分布，然后根据样本对参数进行估计
  • 非参数法：直接根据样本对类条件概率进行估计。knn还可以直接对后验概率进行估计。
• 判别模型不基于后验概率。预先设定含参判别函数，然后从标记样本中学习参数。典型的有神经网络、线性判别、支持向量机

判别分析(判别模型)

判别模型不基于后验概率，而是设计一个函数(黑箱)，对于给定样本作为输入，输出一个类别。当然这个函数在测试前需要进行训练，也就是说这个函数是带有参数的(可调节的)。判别模型训练本质上是利用标记样本进行判别函数参数学习。
如何利用样本进行学习？基本方法是构造准则函数(误差函数)，这个函数包含了样本的标记和模型的输出(也就包含了判别模型的输入和参数)。误差函数原则是样本标记和模型输出一致时(或者近似，对于回归任务)函数值为0或者很小；而当样本标记与模型输出差别很大时，函数值很大。模型参数学习过程就是通过调节参数使得误差函数值尽可能小(模型输出与样本标记一致)。

这张图展示了误差函数。对于样本标记与输出一致的区域(红色)，误差函数为0，其它区域存在误差，要求误差函数对参数可导，这样可以通过求导找到红色的参数空间。三种误差函数分别为分块线性、平滑、陡峭。陡峭的误差函数更容易找到红色区域

最优的学习率最好是经过一次学习就能得到最小值点

线性判别模型

线性判别只支持线性可分情况，否则模型参数学习不收敛。当然线性不可分情况可以改造成线性可分。

二分类器构造多分类器 p64

• 一对一

  
  
  

  (很可能存在不确定区域)

• 逐步一对多：将 c 类问题逐步转化个两类分类问题。 第一个分类器将其中一个类样本与其余各类样本分开，
  接着在其余各类中设计第二个分类器，直至仅剩下两个分类器为止。对新样本判别时，当判别结果对应1个类时，就输出那个类，判别结果为多个类时，继续判别。

• 一对多

  
  
  
  
  
  

  (很可能存在不确定区域)
  改进(线性机器)：对于第i个输出结果，不输入符号函数进行判别，而是看作属于第i类的可能性。对于m个下线性判别函数的值，取值最大的结果对应的类别作为输出，不存在模糊区域。

  
  
  

  线性机器分类策略
  
  线性机器也存在重大缺陷：分类界面只能是
  1 凸的(因为某边界所在超平面必须使得这一类都在一侧，而不可以将同一类的样本分开)
  

  2 单连通的(理由同上，分块是广义上的非凸)
  此时称为线性不可分

  
  
  

  线性机器无法正确分类的数据分布模式
  

  简单的一维情形也无法分类

• 广义线性判别：

1 属性先经过一个(非线性)单值函数，再利用常规的线性判别模型
2 高次推广：加入原先属性的高次项(或交叉项)作为新的属性，仍按照线性判别模型

• 感知器 *p25
  为了简单，仅考虑两类线性可分
  将输入向量进行增广，因此仅需要考虑经过原点的超平面。首先确定正负类，将负类样本乘以系数-1(样本规范化，在样本空间中进行了关于原点的中心对称操作),后面都只考虑处理后的样本(也就是训练样本的无差别对待，包括判断分类正确性和权值更新)。正确样本向量与法向量内积大于0(或夹角小于90°)
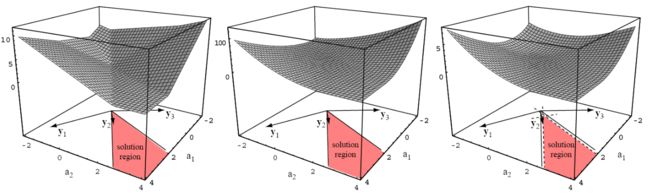
  限制解区域
  • 寻找一个单位长度的解向量 a，能最大化样本到分界面的最小距离(不过这样就复杂了，还要进行极值求解)
  • 寻找一个最小长度的解向量 a，使a‘yi>b. 此时可以将 b 称为间隔 (margin)

在线性可分情形下，满足上述不等式的 a 是无穷多的， 因此需要引入一个准则。仅考虑错分样本作为误差，法向量以批错误样本向量之和的方向进行调整(乘以学习速率)，这样法向量与错误样本之间的夹角减小。

感知机误差函数

权值更新公式

其它感知机误差函数

• 松弛准则

  
  
  
  
  
  

  松弛准则函数的梯度
  
  
  

  松弛准则的更新公式

• 平方误差准则（也就是最常见的线性模型最小二乘解）

  
  
  

  线性模型最小二乘解
  
  

  这里采用梯度下降对求解a(直接求Y的伪逆计算量太大)

  
  
  

  梯度下降法权值更新公式
  
  
  

  Ho-Kashyap Algorithm

• 支持向量机

优点
理论基础强；训练容易；能够避免过拟合
缺点
核函数选择；C参数选择；复杂度高

• 线性可分问题

函数间隔：y(wx+b)，用于表示分类确信度
关于样本点的函数间隔

关于数据集的函数间隔

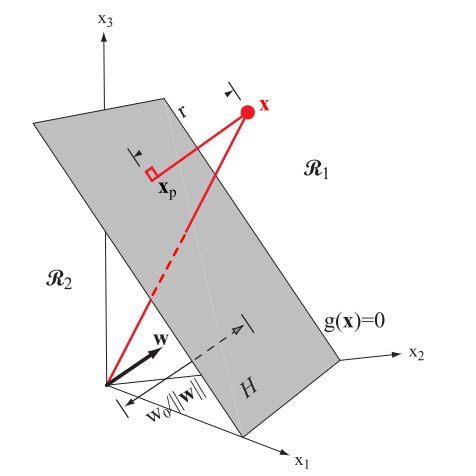
更常用的是几何间隔，物理意义是点到平面的有向距离

平面外一点用其在超平面上的投影以及到超平面的距离表示.注意r为几何距离，有正负

点到平面距离推导

最大化距离的优化问题：

令函数距离为1，转化为等价优化问题：

利用对偶问题求解优化问题

• 线性不可分问题

对于每一个样本引入一个松弛变量，对约束进行放宽。将松弛变量视为代价，加到目标函数中

利用对偶问题求解上述优化问题

求解完上述问题后，对于松弛变量大于0的向量不是支持向量，小于等于0对应的向量是支持向量。
C表示裕量的

-### 非线性划分

因此虽然需要非线性函数将原空间进行非线性映射，但是并不需要具体去求这个函数，只需要求内积形式的核函数

核函数的充要条件是对于任意输入，形成的矩阵是半正定的

• 线性核：输入向量的内积

• 高斯核：输入向量之差的模经过高斯后的输出

  
  
  

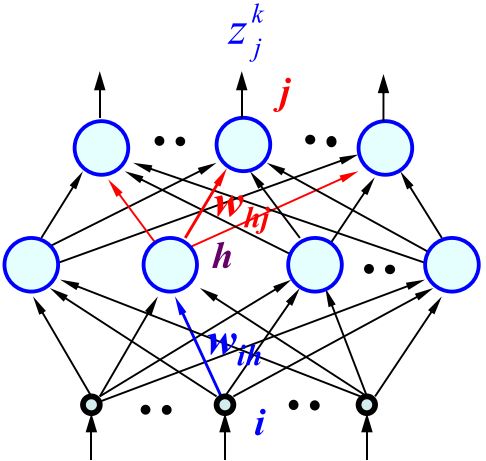
神经网络

误差函数

**输入层节点下标为i,节点输出为x；隐含层节点下标为h,节点输出为y；输出层节点下标为j;节点输出为z**

• RBF网络

  
  
  
  

  一列的径向基函数不相同；一个样本产生p维输出
  

• Hopfield网络
  wij：从结点i 到结点 j 的连接权重，Hopfield网络是对称的
  达到稳定状态。稳定状 态即为网络的输出

• 受限玻尔兹曼机RBM p111
  具有两层结构(完全二部图)，层内结点不相连，信息可双向流动

• 自组织映射网络SOM p109

  
  
  

  竞争层结点之间并没有连接，不过存在一种平面关系。SOM 获胜神经元对其邻近神经元的影响是由近及远的,由兴奋逐渐转变为抑制。在学习算法中，不仅获胜神经元本身要调整权向量(隐层到竞争层的连接权重)，它周围的神经元在其影响下也要不同程 度地调整权重。邻域大小可随时间增长而减小。
  竞争层每一个结点都有各自的权向量，用于与输入计算距离。当输入得到后，每一个竞争层的结点的权重都与之计算距离，然后选出最小的距离对应的结点作为胜出者。

  
  
  

  权向量更新公式

• 自动编码机 Autoencoder

• 线性判别分析（LDA）

  • 两个类别的分类 p60
    将样本空间投影到一维空间，优化目标为

    
    
    
    

求导求解

优化求解

• 多个类别的分类
  将样本空间投影到N-1维空间（类别数减一），优化目标为
  
  
  
  
  
  
  

  LDA不适合的情况

概率模型判别(生成模型)

一个实际为j类样本判为某类i的风险

对于一个准则函数的总体风险

由此导出贝叶斯判别准则：对于每一个样本都选择最小期望代价对应的类别，

最小代价(风险)决策

对于不考虑错判风险，只考虑准确率的任务，上述风险函数具体为0-1代价(风险)：

最小误差率任务：0-1代价(风险)。或者是所有误判代价相等且大于正确的代价

此时最小风险决策具体为最小错误率决策，也就是后验概率最大的对应的类别(类条件概率) p147：

最小误差率决策

• 贝叶斯分类器

贝叶斯分类器与贝叶斯学习有显著区别，前者是通过最大后验概率进行点估计，而后者是进行分布估计。
判别函数(用于计算c个类别对应的风险)：

最小代价(风险)对应的判别函数

最小误差率(0-1风险)分类对应的判别函数

• 最小误差判别：类条件分布假设为多元正态分布

一般类条件概率假设为多元正态分布模型，带入最小误差准则对应的判别函数中，得：

正态分布假设下，最小误差准则对应的判别函数

接着讨论一些情况

• 每一类协方差矩阵都相等、样本属性之间线性无关、各属性方差都相等

  
  
  
  
  

• 每一类协方差矩阵都相等

  
  
  
  
  
• 一般地，每一类协方差不相等
  
  

• 朴素贝叶斯分类器

求类条件概率时，考虑到样本空间太大，因此假设样本各属性之间相互独立，于是类条件概率可以写成属性类条件概率的乘积形式。这样对于每一个概率，样本空间都是一维的，根据样本对求出每一个属性的类条件分布。类的概率按照样本占比进行估计。至此样本学习完毕。

• 对于一个新的样本进行归类
  按照穷举法，对于每一个类别，由于类条件概率分布已知，根据样本属性求出各属性的类条件概率(密度)值，按照上式进行相乘，这样求出所有的类别的后验值后进行排序，将最大值对应的概率进行输出。

• 离散概率分布估计 p153
  离散的概率分布一般直接用样本出现频率来估计，比如类别的先验概率。当样本不充足或分布覆盖不广会导致估计概率为0(连续型概率分布不会遇到这种情况)，很多时候0概率会带来问题(例如朴素贝叶斯分类器，某个类条件属性值为0，那么这个类条件概率直接为0)。因此需要进行平滑修正，一般采用拉普拉斯修正：对于每一类，给每一个离散属性值额外赋予一个样本。于是对于每一类，样本数增加了Ni；总样本数增加N

• 参数法估计类条件概率

给定类别，假设对总体服从特定的概率分布形式，然后基于样本对模型参数进行估计（一般是连续型分布，离散型直接通过出现频率进行估计）。确定参数后，类条件概率p(x|c)就完全确定下来了。
参数估计有两种派别，对应两种方法：

• 极大似然估计法
  由于样本服从总体的分布，对于给定数目的样本，可以构建联合概率分布；由于样本都是独立同分布的，样本联合概率分布可以通过总体概率分布的连乘得到(带参数)。由于样本值已知，可以带入样本联合概率分布中，得到只剩下模型参数为变量的似然函数。使得似然函数值最大的参数即为极大似然估计。

• 贝叶斯参数估计

  
  
  

  贝叶斯后验概率估计核心公式
  
  

  其中参数因为不确定，就当作变量处理，因此具有分布p(θ)，于是按照上述公式进行积分求得类条件分布p(x|D)。而根据数据可以减少参数不确定程度，也就是参数后验概率p(θ|D)。

  
  
  

  贝叶斯学习过程：在数据量越来越多的情况下，参数的不确定程度越来越小，体现为参数的后验分布趋于尖峰状

假设模型参数为正态分布

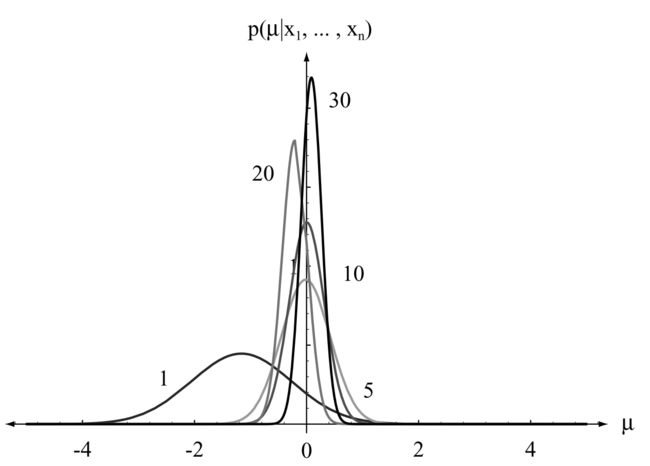
• 单变量情况p(µ|D):

假设类条件分布为正态分布，均值未知，方差已知

均值参数服从已知的正态分布

求得均值参数的后验概率：

根据贝叶斯概率估计公式，积分得到类条件分布：

• 多变量情况

  
  
  

  假设参数和后验概率都服从正态分布，协方差已知，均值向量为参数
  
  
  
  
  
  

• 递归贝叶斯学习

  
  
  

  在线学习：新样本对参数的后验分布更新公式
  
  

  例题：

  
  
  

  假设类条件分布如上，带有未知参数θ
  

  且已知上述参数服从如上分布(先验知识)
  接着观测到数据集D = {4, 7, 2, 8}.
  对于x1 = 4：当θ<4时，p(x|θ)=0；当θ>10时，p(θ|D)=0；当4<θ<10时,p(x|θ)=1/θ，p(θ|D)=c，p(x|θ)p(θ|D)=1/θ. 因此
  
  
  

  第一个数据到达后，参数的分布进行了更新
  
  
  

  参数随数据到来的分布更新

  从贝叶斯参数分布更新公式可以看出，参数在取值空间每一处的值是乘上一个系数（p(x|θ)在此参数值条件下，样本处的概率值），因此区间是进行了放缩，且一旦某点的后验概率更新为0，之后就始终为0. 因此参数的后验概率只会越来越集中，最终形成尖峰。

• EM算法

  • 首先选择参数的初值
  • 
    

    注意是概率分布，因此需要考虑归一化

    
    
    
    

• 非参数法估计类条件概率

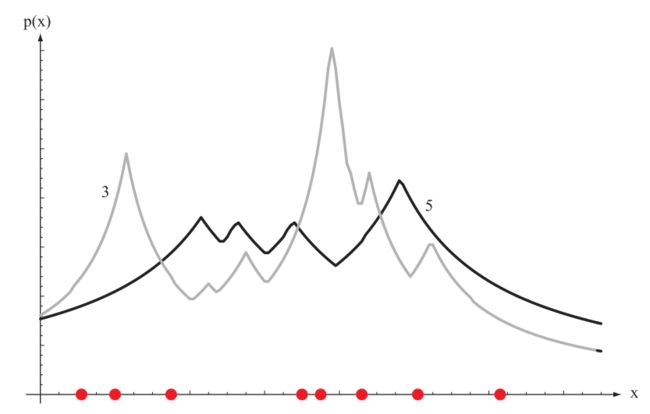
样本空间中某一点处的概率密度用样本在其邻域出现的频率来估计：

其中等式左边为需要估计的某一点处的概率密度，V为此点的一个邻域，两者乘积是一个概率值P（因为概率密度是一个无穷小的概率，在样本空间上积分才是概率值）。k/n表示样本在此邻域内出现的频率。对于给定的数据集，n固定，变量只剩下k和V. 固定k，称为knn估计；固定V，称为Parzen window估计。

• Parzen window

对于输入向量，存在一个分量大于0.5就输出0，否则输出1.

推广：不仅仅是邻域内的样本才对此点有贡献，而是所有样本根据距离远近加权做出贡献。实际上只要满足概率密度要求的函数都可以

推广的delta函数含义为：一个样本，对于给定距离（向量）带来的计数

对于每一个样本，欲测量点处的概率密度为所有样本对此点的概率密度影响之和的平均值

• knn

knn分类器可以直接估计后验概率(类条件概率也可以用knn进行估计)

• 泛化错误率不超过贝叶斯最优估计两倍 p226
  优点：简单好用，容易理解，精度高，理论成熟，既可以用来做分类也可以用来做回归； 可用于数值型数据和离散型数据；无数据输入假定； 对异常值不敏感 。
  缺点：当样本不平衡时有可能导致样本的 K个邻居中大容量类的样本占多数。计算量较大，及时响应性能不行。

k=3，说明包围3个样本最小区间的中心处是一个峰值

k=1时，样本点处的概率密度值为无穷大。除非样本重复，否则其它k>1概率密度值都有界

快速近邻搜索

• 部分距离判断：在进行距离计算时，实际是计算差向量的模，也就是其各个分量的平方和后开方。为了减少乘积运算，一个分量一个分量计算相加，一旦累加和已经超过限定的距离平方后就停止运算，因为距离已经超过限定距离。
• 建立搜索树：思想是：对于明显行不通的方向，试都不要试。好比钥匙丢了，肯定是在最近去的地方找，而不是地毯式找。
• 样本简化：虽然样本数量很多，但是对分类边界有贡献的仅占少数，类似于SVM中支持向量是少数。通过去除冗余样本可以降低计算复杂度。

降维与特征提取

高维有利于不同类别之间的区分

• 高维样本空间带来的困难 p227
  数据样本稀疏：对于一定量的样本，样本空间维数越大，样本就越稀疏。可以反向理解：一定量的高维样本空间中的样本经过降维，样本分布就会密集；低维线性不可分数据在高维线性可分
  距离计算复杂
  泛化困难
  便于可视化
• 降维方法
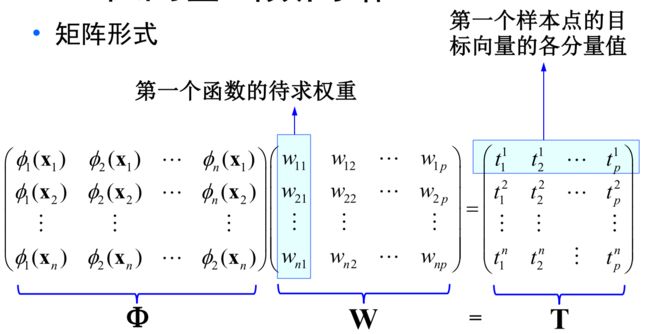
• 针对样本空间，线性变换降维方法（主成分导出）

  • 重构与重构误差 p230

    
    
    

    一个样本（即向量）可以由变换后的空间中的基底和对应坐标的线性组合表示（即重构表示，若重构维数相等，则是同一个向量），与原先空间的坐标表示之间的偏差称为“重构误差”：

    
    
    
    最小化这个误差(x-WW'x)
    
    

  • 投影方差最大化 p230

    
    
    

  • 主成分 p231

上述两个优化问题等价，运用向量求导法则，可得：

显然解与随机向量X的协方差阵的特征值和特征向量有关

PCA算法

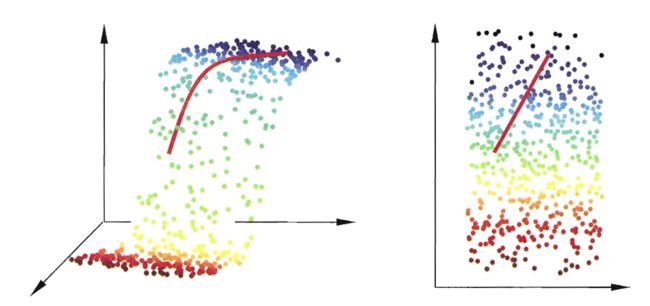
• 保持样本距离的非线性降维方法MDS p227
  测地线距离：沿着空间表面的距离也称“本真距离”。
  高维直线距离：可以脱离表面的高维空间距离

  
  
  

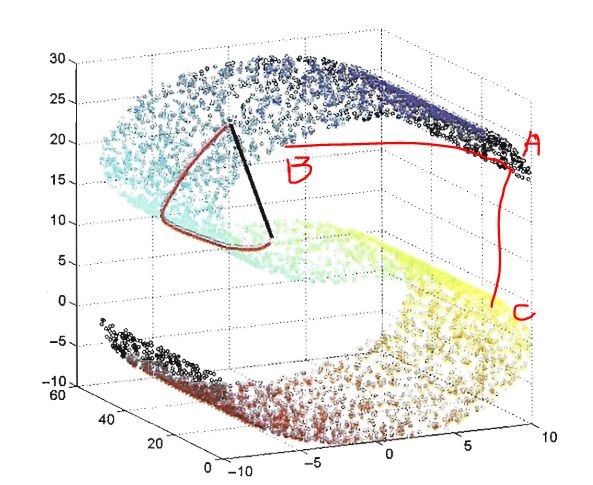
  注意，MDS仅仅是在低维空间保持样本之间距离不变，但是并不保证样本分布与高维分布同构。MDS假设高维直线距离唯一代表样本的近似程度，而实际很多情况下这个假设并不合理：

  
  
  
  如果仅仅使用MDS降维，C点比B点更接近A点，有悖常理。于是引入流行学习(manifold learning)

• 流行学习

  • 等度量映射Isomap
    针对MDS的缺点，Isomap局部采用MDS，得到样本低维分布：

    
    
    

    Isomap算法

  • 局部线性嵌入LLE
    区别与Isomap保持局部样本距离不变，LLE希望保持样本之间相对位置不变

    
    
    

聚类分析

• 混合高斯分布 [pclm] p430
• k-means [pclm] p424
  采用最大似然估计或最小均方误差作为评价聚类的准则函数
  • 最大似然估计: 先假设总体服从k个高斯混合分布，再假设样本属于某类的后验概率服从0-1分布，即距离样本某类中心(因为假设服从高斯分布，因此有中心)最近，属于那类的概率就为1，而属于其他类的概率为0。为了找到各类中心，k-means使用的是最大期望迭代算法(EM): 先随机挑选k个样本作为类中心，利用0-1后验概率，将样本分为k类; 根据得到的k类，计算各类中心，返回上一步。停机条件是类中心不再发生变化。此时类中心就收敛到假设的k个高斯中心了。k-means算法的有效性和收敛性证明参考EM算法。
    
    

    k-means

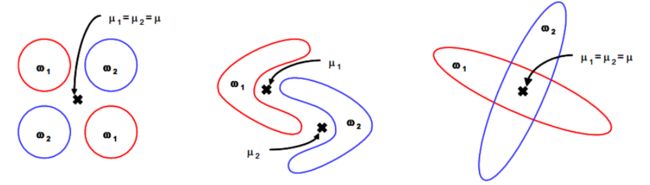
  • 最小均方误差(适用于各类样本平衡，云团分布)：从一个类引出一个样本会减少该类均方误差； 但移入一个样本至一个类会增加该类均方误差。如果减 少量大于增加量，对这样的样本进行移动是有利于总体 误差减少的。也可以进一步改变准则为：类内散度最小；类间散度最大

    
    
    

    样本类调整原则
    

    随机划分成c类，并计算c类的中心；接着随机挑选样本，判断属于哪一类，然后计算这个样本若加入到其它类去引入的误差和在本类中去除所减小的误差；若引入误差小于减小误差，则进行个样本转移，并重新计算涉及到的两个类别的均值；直到无法进行样本转移

kmeans局限性

• 必须事先给定簇的个数，且对初始值敏感

• 不适合于大小相差很大的簇

• 对噪声、孤立数据点很敏感。

• 不适用于总体不满足k个混合高斯分布假设的情况，也就是数据不是一个一个云团分布的。

  
  
  

  散度准则
  
  

  总类内散度迹最小准则：与类均方误差最小准则是等价的。
  类间散度最大准则
  最小化总类内行列式准则

• 谱聚类

实际数据不服从高斯混合分布的情况更加普遍，由此引入谱聚类算法。

• 邻接矩阵(权重矩阵)
  元素为0说明对应的两个顶点之间不相邻（至于顶点自身相似度是多少，后面可以看到对角线元素对结果完全没影响）

  
  
  

  顶点度数
  
  

  |A| 表示一个顶点集中顶点的个数； vol(A) 是顶点集中所有顶点度数之和
  由数据生成邻接矩阵(权重矩阵)的方式

  • ε-neighborhood
  • k-nearest neighbor
  • 全连接

• 拉普拉斯图矩阵

  
  
  

  未标准化的拉普拉斯图矩阵
  

  两种标准化的拉普拉斯图矩阵
  
  

  拉普拉斯图矩阵的特点是：
  1 半正定
  2 0特征值对应的特征向量是全1向量
  3 o特征值的重数表示原图的连接子图个数

  
  
  
  

图切割

补充

• 凸优化问题*p100

  
  
  
• 拉格朗日乘子法 p403
• 对偶问题*p225

常见问题：

• 协方差矩阵不满秩

(a)将协方差矩阵与单位矩阵进行平滑，得到非奇异矩阵。
(b)将协方差矩阵进行正交分解(谱分解)后，将为 0 的特征值置为一个很小的非零值（如 0.001）.

• 距离度量
  距离需要满足的基本性质：
  1 非负性 2 同一性(当且仅当两输入相等时，距离为0) 3 对称性 4 三角不等式(不满足此性质的称为非度量距离p201)

• 向量之间的距离

• Minkowski：适用于有序属性，常用的是Euclidean distance (p=2)；还有曼哈顿距离(p=1)

• tangent distance
  因为OCR常见的仿射变换对欧氏距离影响很大，引入切空间距离。切空间距离不再是两个向量之间的距离，而是样本到另一个样本生成的切空间的距离。切空间是由一些仿射变换"线性"组合（线性系数看作仿射变换参数）形成的空间。一个样本到这个空间的距离也就是其到那个样本的各种仿射变换的最短距离。当然这个切空间得是有限的（也就是仿射变换参数范围有限），比如旋转变换的角度需要控制在一定范围内。缺点是训练计算量大。

  
  
  

• 马氏距离：同一分布的两个样本之间的距离；样本与一总体之间的距离

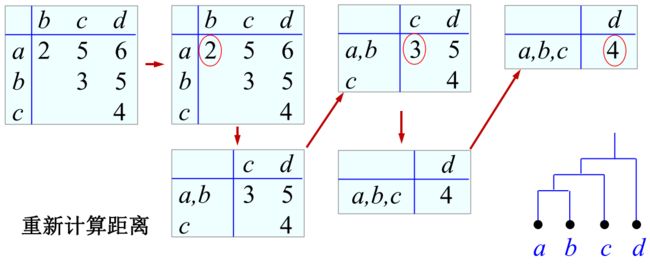
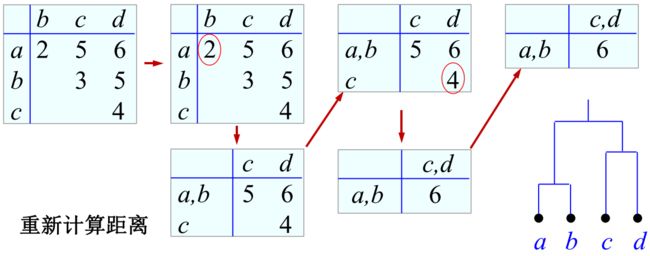
• 样本簇之间的距离
  最大距离、最小距离、平均距离、中心距离

簇与样本之间的距离采用最近距离

簇与样本之间的距离采用最远距离

• 集成学习有效原因
  p181
• 特征选择动机
  1.降维
  2.探索关键因素
• 局部最小问题解跳出思路
  1 重复、随机初始化
  2 模拟退火：以衰减的概率接受次优解
  3 随机梯度下降